Применение метода резолюций для ответов на вопросы

Предположим, что предикат F(х,у), означает  х - отец у, и даны следующие факты об отцовстве:

F(john,. harry) 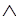F(john, sid) 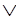F(sid, liz)

Таким образом, есть три единичных (т.е. состоящих из одной литеры) дизъюнкта. Они не содержат переменных или импликаций, а просто представляют базисные факты того самого типа, который подходит для хранения в базе данных.

Введем еще три предиката М(х), S(х,у)  и В(х, у), означающие соответственно, что х - мужчина, что он единокровен с у, что он брат у.

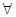( х, у) F(х, у)-->М(х)

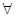(х, у, w) F(х,у)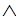F(х, w)-->S(у, w)

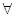(х, у)S(х, у)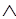М(х)-->В(х, у)

     Они утверждают следующее: 1) все отцы - мужчины; 2)если у детей один отец, то они единокровны; 3) брат - это единокровный мужчина.

Пусть задали вопрос (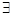z) В(z, harry)? Чтобы найти ответ с помощью метода резолюции, записываем отрицание вопроса (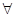z) ~В(z, harry). Затем приводим аксиомы к нормальной форме и записываем каждый дизъюнкт в отдельной строке (так как каждый дизъюнкт истинен сам по себе):

      ~Р(х, у) 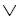 М(х)                                                                                (2 21)

~Р(х, у)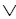 ~F(х, w) 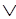S(у, w)                                                           (2 22)

~S(х, у)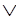 ~M(х)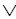 B(х,у)                                                                 (2.23)

F(john, harri)                                                                                     (2.24)

F(john, sid)                                                                                        (2 25)

F(john, liz)                                                                                         (2.26)

~B(z, harri)                                                                                        (2.27)

Не пишем внешних кванторов всеобщности, так как подразумевается, что каждая переменная связана таким квантором.

Константы отличаются от переменных тем, что они либо начинаются буквами из начала латинского алфавита, либо являются именами собственными, такими, как john, harri, sid и liz.

Для применения резолюции необходимо найти для данной пары дизъюнктов такую подстановку термов вместо переменных, чтобы после нее некоторая литера одного из дизъюнктов стала контрарна некоторой литере из другого дизъюнкта (т.е. отличалась от нее лишь отрицанием). Можно делать подстановки, так как все переменные связаны кванторами всеобщности. Если, например, подставим john вместо х и sid вместо у, то получим следующее:

~ F(john, sid)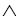~ F(john, w)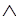S(sid, w).

Можно применить правило резолюции к этому дизъюнкту и (2.25), что дает новый дизъюнкт:

 F(john, w)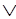 S(sid,w)                                                      (2.28)

из (2.5) и (2.2)                    {john/x, sid/у}

В комментарии справа в фигурных скобках указаны два дизъюнкта использованные в резолюции, и примененная подстановка.

Продолжая, получим

      S(sid, harri)                                                                                      (2.29)

из (2.24) и (2.27) {harri/у}

М(sid)                                                                                                (2.30)

из (2.26) и (2.21) {sid/х, liz/у}

~S(sid, y)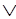B(sid, у)                                                                           (2.31)

из (2.30) и (2.23) {sid/х}

В(sid, harry)                                                                                     (2.32)

из (2.29) и (2.31) {harry/у}

?

из (2.22) и (2.27) {sid/z}                                                                                              (2.33)

Таким образом, вывели единичный дизъюнкт (2.22),выражающий что sid - брат harry, использовав аксиомы и факты (2.24), (2.25), (2.26), имеющиеся в базе данных. Это противоречит отрицанию вопроса, которое утверждает, что harry не имеет братьев.

Если хотим знать, кто же брат Ьаггу, то должны следить за сделанными подстановками. Это можно сделать, введя новую литеру – так называемую литеру ответ с предикатом Answer(ответ).

Тогда вместо ~В(z, harri) напишем

                                   ~В(z, harri) 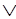 Answer(z).                                     (2.27a)

Теперь продолжим процесс резолюции не до получения пустого дизъюнкта, а до получения единичного дизъюнкта с предикатом Answer, которая запоминает подстановку для z, нужную для резолюции с дизъюнктом В(z, harri). Тогда (2.33) примет вид Answer(sid) из (2.22) и (2.27а) {sid/z}.

Полученный ответ означает, что sid – брат harry. При другой исходной информации получили бы вместо единичного дизьюнкта, скажем Answer(sid)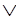Answer(fred).

Даже если провести резолюцию в несколько ином порядке, то получим тот же самый ответ. Допустим, что дошли до строки (2.21) так же, как и раньше, но затем применили (2.27а) вместо (2.27).

      ~S(х, harry)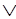 ~М(х)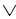 Ansver(х) (2.21)

из   (2.27а)   {х   /z}   и   (2.23)

{harry/у}                                                                                            (2.21)

S(sid, harri)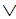 Answer(sid)                                                                 (2.22)

из (2.30) и (2.31) {sid/х}

Answer(sid)                                                                                         (2.33)

из (2.32) и (2.29)

Однако если производить подстановки в иной последовательности, то попадаем в затруднительное положение:

      ~ F(john, w)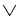 S(sid,w)                                                                      (2.28)

из (2.26) и (2.22) {john/x, harry/x)

S(hагrу, sid)                                                                                        (2.29)

из (2.25) и (2.28) {sid/w}

Проблема в том, что доказали S(hаггу, sid) вместо дизъюнкта S(sid, hаггу), который нужен нам для резолюции с (2.32). Эту трудность можно обойти, введя дополнительную аксиому:

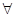      ( х, у) S(х, у) -->S(у, х),

которая в нормальной форме имеет вид

      ~ S(х, у)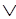 S((у, х)                                                                             (2.34)

К сожалению, далее нужно проявлять осторожность, чтобы не попасть в следующий бесконечный цикл:

     S(sid, hагrу)                                                                                        (2.35)

из (2.29) и (2.34) {hагrу/х, sid/у}

S(hагrу, sid)                                                                                        (2.36)

из (2.35) и (2.34) {sid/х, harry/у}

S(sid, hагту)                                                                                        (2.37)

из (2.36) и т.д.

Это показывает, что необходимо тщательно планировать поиск доказательства, если хотим сохранить надежду искать его автоматически.