Применяется всего одно правило вывода, что позволяет не запоминать многочисленных правил вывода и тавтологии. Это- правило резолюции, которое приведено в таблице 2.1 вместе с уже известными правилами.
Таблица 2.1
|
Резолюция |
Цепное правило |
Модус поненс |
Из Х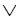 А А |
Из ~Х-->А |
А |
И Y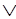 ~А ~А |
И А-->Y |
А-->Y |
Получаем Х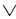 Y Y |
Получаем ~Х-->Y |
Y |
Оно позволяет соединить две формулы, удалив из одной атом А а из другой ~А. Из приведенной выше таблицы видно, что правило резолюции можно рассматривать как аналог цепного правила в применении к формулам, находящимся в конъюнктивной нормальной форме В данном случае цепное правило записано в форме, эквивалентной приведенной ранее, но более удобной для сопоставления с правилом резолюции. Правило модус поненс можно считать частным случаем правила резолюции для случая ложного X.
Правило резолюции применяем следующим образом.
Используем доказательство от противного и допускаем отрицание заключения.
Приводим все посылки и отрицание заключения, принятого в качестве дополнительной посылки, к конъюнктивной нормальной форме.
а) Устраняем символы <-->и--> с помощью эквивалентностей
(А<-->В) = (А-->В) 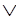 C)
C)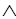 (В-->А);
(В-->А);
A-->В = ~А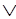 В
В
б) Продвигаем отрицания внутрь с помощью закона де Моргана.
в) Применяем дистрибутивность
А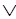 (B
(B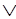 C)=(A
C)=(A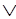 B)
B)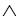 (A
(A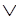 C).
C).
Этот метод приведения формул к виду, удобному для применения метода резолюции, обладает рядом серьезных недостатков, так как применение дистрибутивности, часто приводит к экспоненциальному разбуханию- испытуемой формулы и разрушает ее структуру. В пропозициональном случае лучше привести к конъюнктивной нормальной форме саму исходную формулу, что сразу решает вопрос о ее тавтологичности.
Зачастую гораздо целесообразнее упрощать формулу к виду, постепенно уменьшая ее глубину путем введения новых атомов, обозначающих ее части.
Теперь каждая посылка превратилась в конъюнкцию дизъюнктов, быть может, одночленную. Выписываем каждый дизъюнкт с новой строки; все дизъюнкты истинны, так как конъюнкция истинна по предположению.
Каждый дизъюнкт- это дизъюнкция (возможно, одночленная), состоящая из предложений и отрицаний предложений. Именно к ним применим метод резолюций. Берем любые два дизъюнкта, содержащие один и тот же атом, но с противоположными знаками, например
Х 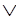 Y
Y 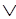 Z
Z 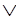 ~P, X
~P, X 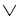 P
P 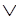 W.
W.
Здесь Р - как раз тот атом, о котором шла речь. Применяем правило резолюции с атомом Р в роли А из этого правила, т.е. "отрезаем" Р от двух данных дизъюнктов:
(Х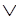 Y
Y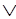 Z)
Z)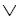 (Y
(Y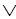 W)=X
W)=X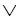 Y
Y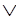 Z
Z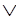 W.
W.
Это правило легко применять, так как оно сводится к простому удалению членов дизъюнктов.
Из Х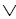 A,~A
A,~A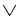 Y выводим Х
Y выводим Х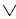 Y.
Y.
Из A, ~A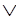 Y выводим Y.
Y выводим Y.
Продолжаем этот процесс, пока не получится Р и ~Р для некоторого атома Р. Применяя резолюцию и к ним, получим пустой дизъюнкт, выражающий противоречие, что завершает доказательство от противного.
Из Р, ~Р выводим ложь.
Пустой дизъюнкт обычно записывается в виде квадрата ?.
В качестве примера рассмотрим доказательство соотношения:
P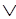 Q, P-->R, Q-->S|-R
Q, P-->R, Q-->S|-R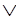 S
S
- Приводим посылки к нормальной форме и выписываем их на отдельных строках.
P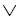 Q, (2.12)
Q, (2.12)
~ P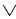 R, (2.13)
R, (2.13)
~Q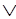 S (2.14)
S (2.14)
- Записываем отрицание заключения и приводим его к нормальной форме.
~(R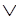 S)= ~R
S)= ~R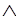 ~S
~S
~R (2.15)
~S (2.16)
- Выводим пустой дизъюнкт с помощью резолюции.
~Р из (2.15) и (2.13) (2.17)
Q из (2.17) и (2.12) (2.18)
~Q из (2.16) и (2.14) (2.19)
? из (2.18) и (2.19) (2.20)
По сравнению с классической логикой метод резолюции имеет ряд преимуществ.
- Не приходится применять эквивалентности для того, чтобы переставлять члены дизъюнкции Р
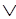 Q для получения Q
Q для получения Q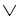 P и т.д. Это происходит отчасти потому, что все приводится к нормальной форме с самого начала, а отчасти потому, что для правила резолюции неважно положение отрезаемого атома в дизъюнкте.
P и т.д. Это происходит отчасти потому, что все приводится к нормальной форме с самого начала, а отчасти потому, что для правила резолюции неважно положение отрезаемого атома в дизъюнкте.
- Нужно помнить всего одно правило.
Применение этого правила легко автоматизировать, т.е. запрограммировать для компьютера. Однако в случае длинного доказательства легко зациклиться, а однородные обозначения делают все дизъюнкты похожими друг на друга, так что трудно удерживать в памяти их смысл и выбирать нужный дизъюнкт.
