Доказательство с введением допущения

Для доказательства импликации вида А-->В допускается, что левая часть А истинна, т.е. А принимается в качестве дополнительной посылки, и делаются попытки доказать правую часть, В.

Сам метод опирается на две важные теоремы о доказательствах [60].

Теорема 1. А |- В тогда и только тогда, когда |- А--> В.

Эта теорема утверждает, что доказуемость заключения В из допущения А эквивалентна доказуемости импликации А--> В без каких-либо дополнительных допущений.

Теорема 2. А1,А2,...,Аn |- В тогда и только тогда, когда 

|-(А1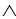А2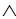 ... 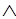An) --> В.

Эта теорема получается из предыдущей и того факта, что все посылки А1,...,Аn истинны тогда и только тогда, когда истинна их конъюнкция (основное свойство связки И).

Наконец, очень полезная эквивалентность |= (X-->(Y-->Z))<-->(X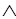Y-->Z).

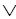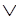Она легко доказывается с помощью соотношений булевой алгебры  так как левая и правая части сводятся к ~X~Y Z.

Рассмотрим пример доказательства с введением допущения.

Если А1. А2,..., Аn, Р |-Q,

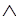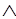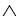то |-А1А2...АnР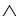-->Q) в силу теоремы 2,

откуда |-А1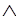A2...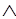Аn)-->(P-->Q) в силу эквивалентности,

откуда |-А1,А2,...,Аn |-Р-->Q) в силу теоремы 2.