Элементы теории множеств

Большую часть понятий дискретной математики можно определить с помощью понятия множества. Множество - основополагающее, первичное и неопределяемое понятие математики. Множеством принято называть набор, совокупность некоторых объектов, при этом природа самих объектов, составляющих то или иное множество нас и не будет интересовать. Создатель теории множеств Георг Кантор давал следующее определение множества - "множество есть многое, мыслимое нами как целое."

Объекты, из которых состоит то или иное множество принято называть элементами этого множества. В математике употребляются следующие синонимы термина множество - система, класс, совокупность. Как уже говорилось, множества могут быть самой различной природы, например, множество всех деревьев в нашем родном городе на 29 июля 1974 года, в качестве другого примера множества можно принять следующее определение множество всех студентов, сидящих сейчас в соседней аудитории. В первом примере элементами множества являются деревья, а во втором студенты.

В математике рассматриваются более специфические множества, состоящие из чисел, кривых, множеств чисел и т.д. Множества принято обозначать большими буквами латинского алфавита, а элементы этих множеств - маленькими буквами латинского алфавита. Например, множества A, B, ... X, Y, Z и соответственно элементы a, b,... x, y, z.

Приведем стандартные обозначения для наиболее часто используемых числовых множеств:
- множество натуральных чисел, = {1,2,3,... };
- множество целых чисел, =  
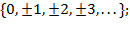
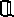- множество рациональных чисел,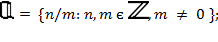  
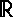- множество действительных (вещественных) чисел.
В математике принято использовать следующие обозначения:
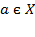 - "элемент a принадлежит множеству X";
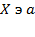 - "множество X содержит элемент a", что, вообще говоря, тоже самое;
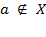 - "элемент a не принадлежит множеству X";
- квантор произвольности: 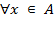 - "для любого элемента x множества A";
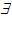- квантор существования:  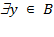- "существует (найдется) элемент y из множества B";
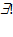 - квантор существования и единственности:  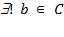- "существует единственный элемент b из множества C";
: - "такой, что;    обладающий свойством", обычно таким значком дополняется предыдущий квантор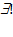
--> - квантор следования - "если ..., то ...";
<--> - квантор равносильности - "тогда и только тогда";

Множество может содержать много элементов, а может лишь несколько, например, множество русских букв содержит ровно 33 элемента. Множество натуральных чисел содержит бесконечно много элементов. Может быть и предельный случай, когда множество вообще не содержит элементов, например, множество действительных корней уравнения x⁴+8 = 0.

Определение. Множество не содержащее ни одного элемента называется пустым множеством и обозначается .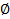
В общем случае множества бывают конечные и бесконечные.

Определение. Конечное множество это такое множество, для которого существует натуральное число равное числу его элементов.
Например, множество русских букв - конечное множество, так как существует натуральное число 33, равное числу элементов этого множества.
Определение. Множество, не являющееся конечным называется бесконечным множеством.

Уже рассмотренное нами множество натуральных чисел - бесконечное множество, поскольку нет такого натурального числа, которое равнялось бы числу его элементов.

Если множество A - конечное множество, то через |A | принято обозначать число его элементов и называть |A | мощностью множества A. Понятие мощности вводится и для бесконечных множеств, однако мы будем рассматривать его немного позднее.

Пример. Пусть множество A состоит из следующих элементов { январь, февраль, март, апрель, май, июнь, июль, август, сентябрь, октябрь, ноябрь, декабрь } - это множество месяцев одного года. Понятно, что мощность |A| заданного таким образом множества A равна 12. Это число элементов множества A или, что то же самое количество месяцев одного года.

Определение. Два конечных множества A и B называются равными, если они состоят из одних и тех же элементов. Если множества A и B равны, то мы будем писать A = B, в противном  случае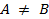  

Таким образом, мы получили следующее определение:

Определение. Два конечных множества A и B не равны между собой, если в множестве A есть элемент не принадлежащий множеству B или наоборот.
Согласно такого определения равенства множеств мы естественно получаем, что все пустые множества равны между собой или что то же самое, что существует только одно пустое множество.

Примеры. a) Множества { 0, 1, 2} = { 1, 2, 0} равны между собой и поэтому между ними мы можем поставить знак равенства - они конечны и состоят из одних и тех же элементов.

b) Рассмотрим теперь три множества A = { 0, 1 }, B = {{ 0, 1 },2} и C = {{{ 0, 1 }, 2} 3}. Между этими множествами справедливы следующие соотношения .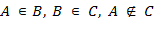

Существует два основных способа задания множеств: перечисление и описание. Множество можно задать перечислив все его элементы, а также при помощи объявления свойства, определяющего какие элементы принадлежат, а какие не принадлежат описываемому множеству.

Давайте, вспомним пример с месяцами. Мы задавали это множество перечислением всех его элементов: январь, февраль, .... Перечислением можно задать только конечные множества. Трудно перечислить все натуральные числа от 2 до 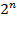. Описание этого множества в предыдущем предложении выделено наклонным шрифтом. Бесконечные множества можно задать только описанием свойства его элементов. Вернитесь немного назад и посмотрите, как мы определяли множество рациональных чисел 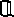, фактически это было описание свойств его элементов. Множество  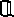мы задавали описанием.