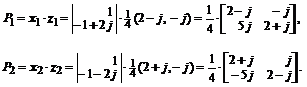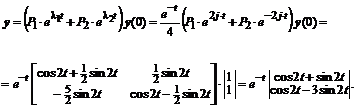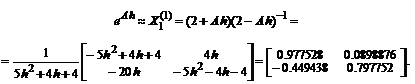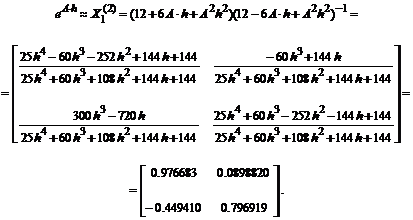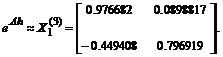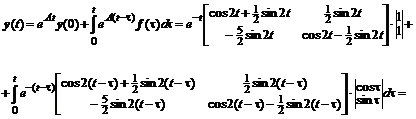В качестве примера построим переходный процесс для системы уравнений:
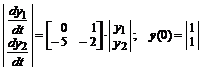 .
.
Эта система может быть представлена дифференциальным уравнением второго порядка относительно переменной 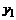 :
:
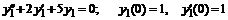 ,
,
или относительно переменной 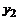 :
:
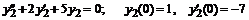 .
.
Характеристическое уравнение 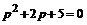 имеет два комплексных корня:
имеет два комплексных корня: 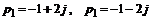 . Общее решение этих уравнений будет:
. Общее решение этих уравнений будет:
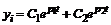 ,
,
где 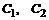 – постоянные, которые вычисляются по заданным начальным условиям путем решения системы уравнений:
– постоянные, которые вычисляются по заданным начальным условиям путем решения системы уравнений:
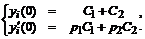
Несложные преобразования приводят к следующим точным решениям этого уравнения для двух различных наборов начальных условий:
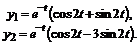
Получим такое же аналитическое решение векторного переходного процесса в форме экспоненциальной функции, используя спектральное разложение матрицы по собственным значениям.
Характеристический полином заданной матрицы имеет вид:
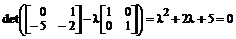 .
.
Собственные значения матрицы (корни характеристического уравнения) и собственные векторы равны:
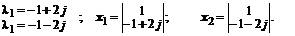
Проекторы находим матричным произведением левых и правых собственных векторов. Для этого обратим матрицу 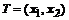 и в качестве левых собственных векторов возьмем ее строки:
и в качестве левых собственных векторов возьмем ее строки:
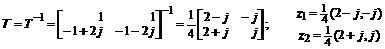
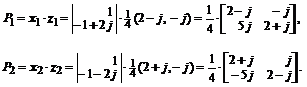
Векторное аналитическое решение имеет вид:
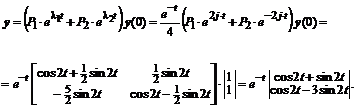
Решение совпадает с точным решением уравнений второго порядка.
Для численного построения векторного переходного процесса по заданному векторно-матричному уравнению с использованием Падэ-аппроксимации матричной экспоненты дробно-рациональными выражениями первого, второго и третьего порядков, вычислим сначала эти аппроксимирующие матрицы:
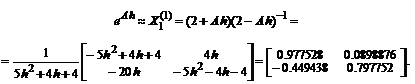
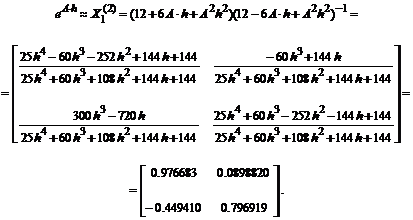
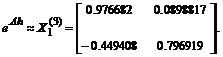
Вектор приближенного решения вычислим по рекуррентной формуле, в которую, для демонстрации влияния на точность результата, поочередно подставим каждое из трех приведенных выше приближений к матричной экспоненте:
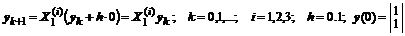 :
:
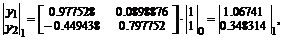
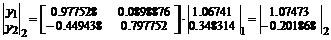 . . .
. . .
В таблице помещены численные значения переходных процессов, полученные для трех названных случаев аппроксимации матричной экспоненты вместе с точным аналитическим решением.
t |
Аналитическое
решение
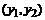 |
Аппроксимация
Падэ порядка 1
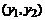 |
Аппроксимация
Падэ порядка 2
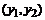 |
Аппроксимация
Падэ порядка 3
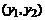 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0.1 |
1.066 |
0.3475 |
1.0670 |
0.3483 |
1.0660 |
0.3475 |
1.066 |
0.3475 |
0.2 |
1.072 |
-0.2023 |
1.0740 |
-0.2018 |
1.0720 |
-0.2023 |
1.072 |
-0.2023 |
0.3 |
1.029 |
-0.6434 |
1.0320 |
-0.6440 |
1.0290 |
-0.6434 |
1.029 |
-0.6434 |
0.4 |
0.9478 |
-0.9755 |
0.9513 |
-0.9778 |
0.9478 |
-0.9755 |
0.9478 |
-0.9755 |
0.5 |
0.8380 |
-1.203 |
0.8420 |
-1.207 |
0.8380 |
-1.203 |
0.8380 |
-1.203 |
0.6 |
0.7103 |
-1.335 |
0.7145 |
-1.341 |
0.7102 |
-1.335 |
0.7102 |
-1.335 |
0.7 |
0.5737 |
-1.383 |
0.5779 |
-1.391 |
0.5737 |
-1.383 |
0.5737 |
-1.383 |
0.8 |
0.4360 |
-1.360 |
0.4398 |
-1.369 |
0.4360 |
-1.360 |
0.4360 |
-1.360 |
0.9 |
0.3035 |
-1.280 |
0.3068 |
-1.290 |
0.3035 |
-1.280 |
0.3035 |
-1.280 |
1.0 |
0.1814 |
-1.156 |
0.1839 |
-1.167 |
0.1814 |
-1.156 |
0.1814 |
-1.156 |
Из сопоставления результатов можно сделать заключение, что аппроксимация экспоненты дробно-рациональной матричной функцией второго порядка позволяет при прочих равных условиях получать решение с 5-6-ю достоверными десятичными знаками.
Численное решение неоднородного дифференциального уравнения в векторно-матричном представлении проведем с прежней однородной частью в уравнении, но применим рекуррентные формулы с интегрированием по методу прямоугольников, трапеций и парабол:
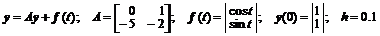 .
.
Матричная экспонента для рекуррентных формул в данном примере бралась в абсолютно точном аналитическом представлении, полученном для этой матрицы выше (числовое представление для h=0.1):
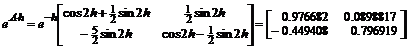 .
.
Аналитическое решение в векторно-матричной форме записи имеет следующий вид:
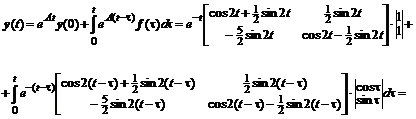
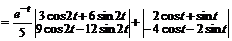 .
.
В таблице приведены результаты вычисления переходных процессов для векторно-матричного неоднородного дифференциального уравнения по формуле аналитического решения и трем рекуррентным выражениям, использующим различные квадратурные формулы интегрирования. Для заполнения таблицы с шагом 0.1 по третьей рекуррентной формуле второе значение (для t=0.1) было получено вычислением с шагом 0.05. Эти первые два значения использовались в качестве начальных значений двух рекуррентных процессов, вычислявших очередные значения с шагом 0.2 .
t |
Точное решение
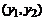 |
Интегрированиепо формуле пря-моугольников |
Интегрирование по формуле трапеций |
Интегрирование по формуле парабол |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0.1 |
1.16576 |
0.328872 |
1.16422 |
0.302569 |
1.16514 |
0.330031 |
1.16576 |
0.328872 |
0.2 |
1.26681 |
-0.271328 |
1.26234 |
-0.318851 |
1.26567 |
-0.269062 |
1.26680 |
-0.271346 |
0.3 |
1.31004 |
-0.785828 |
1.30176 |
-0.849621 |
1.30849 |
-0.782554 |
1.31125 |
-0.802579 |
0.4 |
1.30354 |
-1.20604 |
1.29100 |
-1.28147 |
1.30167 |
-1.20189 |
1.30354 |
-1.20605 |
0.5 |
1.25599 |
-1.52886 |
1.23917 |
-1.61178 |
1.25389 |
-1.52399 |
1.25944 |
-1.55740 |
0.6 |
1.17619 |
-1.75579 |
1.15542 |
-1.84257 |
1.17395 |
-1.75039 |
1.17618 |
-1.75580 |
0.7 |
1.07265 |
-1.89209 |
1.04854 |
-1.97973 |
1.07033 |
-1.88633 |
1.07991 |
-1.92961 |
0.8 |
0.953246 |
-1.94585 |
0.926640 |
-2.03193 |
0.950907 |
-1.93991 |
0.953243 |
-1.94586 |
0.9 |
0.825009 |
-1.92713 |
0.796891 |
-2.00986 |
0.822699 |
-1.92120 |
0.837584 |
-1.97248 |
1.0 |
0.693974 |
-1.84722 |
0.665412 |
-1.92534 |
0.691726 |
-1.84145 |
0.693977 |
-1.84722 |
Аналогичные формулы построения вычислительных процедур могут быть выведены для уравнений с переменными коэффициентами и нелинейных уравнений. Однако обеспечение устойчивости и точности построения переходных процессов в таких случаях решается для каждой конкретной задачи отдельно.

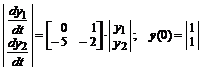 .
.