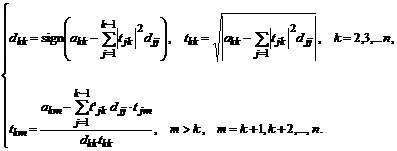Использование разложения на взаимно транспонированные треугольные матрицы при решении систем алгебраических уравнений называется метод квадратного корня.
Метод разложения на транспонированные треугольные матрицы имеет модификацию, заключающуюся в выделении в произведении диагональной матрицы D с элементами на диагонали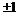 
. Таким образом, для исходной матрицы, которая может быть и эрмитовой (симметричной и комплексно сопряженной), разыскивается произведение трех матриц: 
.
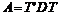Каждое km-тое уравнение, определяется произведением k-того вектора-строки левой треугольной матрицы на диагональную матрицу, умноженную на m-тый столбец правой треугольной матрицы, и имеет вид:
.
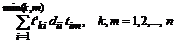Для однозначного разложения, учитывая комплексную сопряженность симметричных элементов треугольных матриц, в первом уравнении (i=1), имеющем вид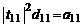 
, полагают 
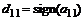. В этом случае
.
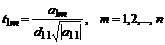Аналогично, отделяя знак диагонального элемента диагональной матрицы от его модуля, можно получить формулы для вычисления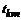 
:
