Эквивалентные преобразования матрицы в произведение более простых, приводящих к решению или облегчающих его получение, начнем с рассмотрения метода обращения матрицы. Так как в общем виде решение системы представляется через обратную матрицу в виде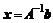 
, то предположим, что
,
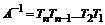тогда, умножив справа равенство на матрицу A , получим
.
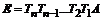Отсюда можно сделать вывод, что матрицы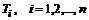 
должны последовательно сводить матрицу A к единичной. Если преобразующую матрицу выбрать так, чтобы только один ее столбец отличался от единичных векторов-столбцов, т.е. 
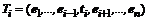, то вектор-столбец 
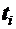можно сформировать таким, чтобы при умножении на текущую преобразуемую матрицу 
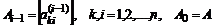в последней i-тый столбец превратился в единичный 
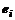. Для этого берут
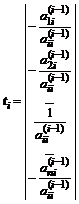и тогда 
.
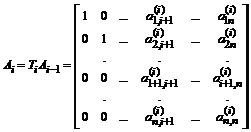Фактически это матричное произведение преобразует все компоненты промежуточной матрицы по формулам, применяемым в методе исключения Гаусса. Особенность этого процесса заключается в том, что диагональные элементы исходной и всех промежуточных матриц не должны быть нулевыми.
Кроме обратной матрицы, равной произведению всех T-матриц, теперь можно получать и решения уравнений для любого вектора в правой части.
