Проекторы матрицы можно также вычислить, воспользовавшись интерполяционным многочленом Лагранжа с матричным аргументом:
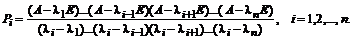
По известному спектру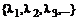 
проекторы матрицы можно найти и методом неопределенных коэффициентов. Для чего выбирают такие функции от матрицы A, которые вычисляются очевидным образом, например, такие:
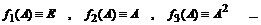
Записывая разложение для каждой функции, получим следующую систему линейных уравнений относительно проекторов:
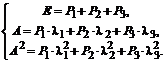
В случае, когда в спектре матрицы имеются кратные собственные значения, вычисление проекторов осуществляется по интерполяционным формулам Лагранжа, учитывающим еще и заданные значения производных в отдельных точках. Разложение матричной функции по значениям ее на спектре в этом случае имеет вид:
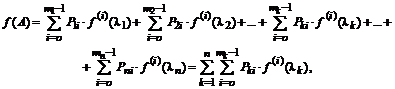
где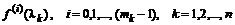 
– значения i-тых произ-водных функции в точках, соответствующих различным (не кратным) корням характеристического многочлена,
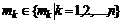– число кратных корней 
,
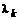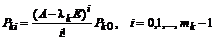– проекторы кратных корней, в выражении которых содержатся
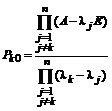- проекторы различных корней.
