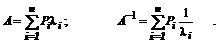Пусть теперь задана некоторая матричная функция от матрицы A:
.
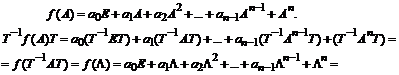
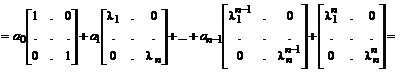
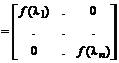С другой стороны очевидно и обратное
,
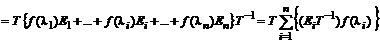где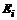 
– матрица с одной единицей на i-том месте диагонали (
).
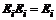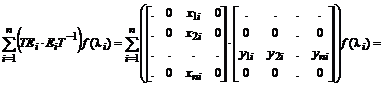
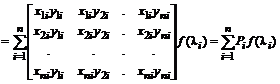
где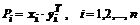 
– проекторы матрицы A, образуемые умножением одноименных правых и левых собственных векторов по правилам умножения прямоугольных матриц с размерами соответственно 
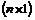и 
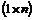. Сумма проекторов 
.
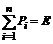Проекторы обладают свойствами идемпотентных матриц, т.е. матриц, все степени которых равны первой. Для невырожденных проекторов (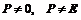
) матрицы A (
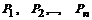) справедливо:
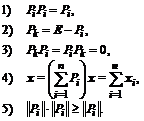
Представление функции от матрицы A в виде взвешенной суммы проекций называется спектральным разложением матричной функции по собственным значениям матрицы A:
.
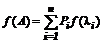Если в качестве матричных функций взять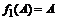 
и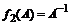 
, то их спектральные разложения будут следующими:
