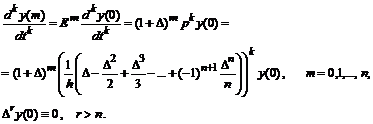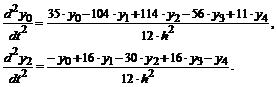Исходные дифференциальные уравнения во многих физических и технических применениях решаются для случаев, когда заданы значения искомых функции и/или ее производных в различных точках интервала интегрирования и, в частности - на концах интервала. Такого рода уравнения в обыкновенных производных или системы из таких уравнений называются краевой задачей.
Общим методом решения краевой задачи является преобразование ее в систему алгебраических уравнений относительно множества неизвестных значений искомой функции, выбранных в точках, равномерно расположенных на оси абсцисс, т.е. заданных на сетке известных значений независимой переменной.
Для линейной системы уравнений первого порядка, записанной в матричной форме относительно вектора 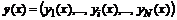 как
как
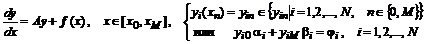 ,
,
обязательно задается полный набор краевых условий 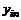 , включающий хотя бы одно значение
, включающий хотя бы одно значение 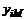 , или набор комбинаций из значений
, или набор комбинаций из значений 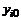 и
и 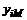
Обычно задаваемое граничное значение совмещается с тем или иным n-ным сеточным значением независимой переменной. Это позволяет обходиться без преобразования граничных условий к ближайшей точке сетки.
Векторы 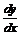 ,
, 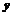 ,
, 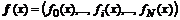 и матрица
и матрица 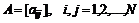 в общем случае приводятся к единичному интервалу изменения независимой переменной с помощью линейного преобразования
в общем случае приводятся к единичному интервалу изменения независимой переменной с помощью линейного преобразования 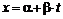 , в котором
, в котором 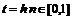 с шагом по оси абсцисс равном
с шагом по оси абсцисс равном 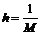 . Благодаря этому производные в левых частях единообразно заменяются (M+1)-точечными конечно-разностными выражениями через искомые значения решения:
. Благодаря этому производные в левых частях единообразно заменяются (M+1)-точечными конечно-разностными выражениями через искомые значения решения:
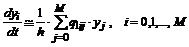 .
.
Многоточечные представления производных получаются путем применения существующих соотношений между операторами дифференцирования, конечных разностей и сдвига:
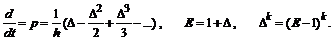
Чтобы выразить значение производной порядка k в m-той точке целочисленного интервала [0, n] через ординаты функции 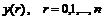 необходимо выполнить следующие операторные преобразования:
необходимо выполнить следующие операторные преобразования:
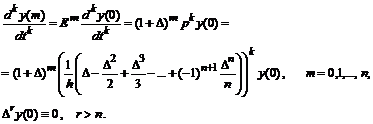
Заменив конечно-разностные операторы 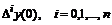 (после приравнивания нулю разностей со степенями выше n) выражениями с оператором сдвига
(после приравнивания нулю разностей со степенями выше n) выражениями с оператором сдвига 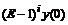 и вспомнив, что
и вспомнив, что 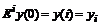 , получим в результате для k-той производной в m-той точке взвешенную сумму из ординат искомой функции:
, получим в результате для k-той производной в m-той точке взвешенную сумму из ординат искомой функции:
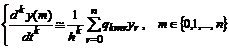 .
.
Погрешность аппроксимации дифференциального оператора конечно-разностным оператором для центральной точки (m=n/2) пропорциональна с наименьшим коэффициентом величине 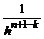 и c наибольшим – для точек конца интервала.
и c наибольшим – для точек конца интервала.
Часто применяемые выражения конечно-разностной аппроксимации производных первого и второго порядков по трем-семи равномерно расположенным точкам приведены ниже в таблицах в виде коэффициентов, стоящих перед соответствующими ординатами функции. В левом верхнем углу таблиц записан общий множитель, а в крайней правой колонке – коэффициенты k1, k2для формул погрешности.
Трех точечная аппроксимация первой производной
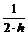
|
y(0) |
y(1) |
y(2) |
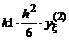
|
y’(0) |
-3 |
4 |
-1 |
2 |
y’(1) |
-1 |
0 |
1 |
-1 |
y’(2) |
1 |
-4 |
3 |
2 |
Четырех точечная аппроксимация первой производной
|
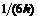 |
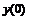
|
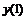
|
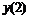
|
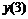
|
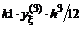
|
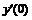
|
-11 |
18 |
-9 |
2 |
-3 |
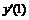
|
-2 |
-3 |
6 |
-1 |
1 |
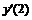
|
1 |
-6 |
3 |
2 |
-1 |
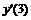
|
-2 |
9 |
-18 |
11 |
3 |
Пятиточечная аппроксимация первой производной
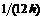
|
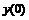
|
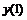
|
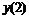
|
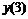
|
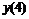
|
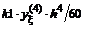
|
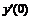
|
-25 |
48 |
-36 |
16 |
-3 |
12 |
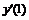
|
-3 |
-10 |
18 |
-6 |
1 |
-3 |
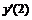
|
1 |
-8 |
0 |
8 |
-1 |
2 |
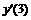
|
-1 |
6 |
-18 |
10 |
3 |
-3 |
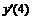
|
3 |
-16 |
36 |
-48 |
25 |
12 |
Шести точечная аппроксимация первой производной
|
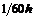 |
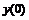
|
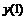
|
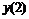
|
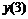
|
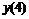
|
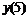
|
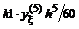
|
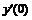
|
-137 |
300 |
-300 |
200 |
-75 |
12 |
-10 |
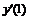
|
-12 |
-65 |
120 |
-60 |
20 |
-3 |
2 |
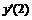
|
3 |
-30 |
-20 |
60 |
-15 |
2 |
-1 |
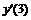
|
-2 |
15 |
-60 |
20 |
30 |
-3 |
1 |
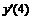
|
3 |
-20 |
60 |
-120 |
65 |
12 |
-2 |
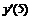
|
-12 |
75 |
-200 |
300 |
-300 |
137 |
10 |
Семи точечная аппроксимация первой производной
|
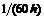 |
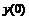
|
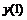
|
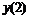
|
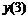
|
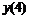
|
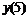
|
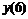
|
 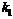
|
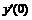
|
-147 |
360 |
-450 |
400 |
-225 |
72 |
-10 |
60 |
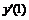
|
-10 |
-77 |
150 |
-100 |
50 |
-15 |
2 |
-10 |
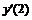
|
2 |
-24 |
-35 |
80 |
-30 |
8 |
-1 |
4 |
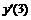
|
-1 |
9 |
-45 |
0 |
45 |
-9 |
1 |
-3 |
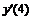
|
1 |
-8 |
30 |
-80 |
35 |
24 |
-2 |
4 |
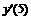
|
-2 |
15 |
-50 |
100 |
-150 |
77 |
10 |
-10 |
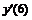
|
10 |
-72 |
225 |
-400 |
450 |
-360 |
147 |
60 |
Трех точечная аппроксимация второй производной
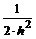
|
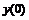
|
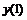
|
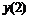
|
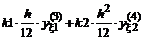
|
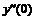
|
1 |
-2 |
1 |
-12 , 2 |
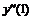
|
1 |
-2 |
1 |
0 , -1 |
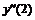
|
1 |
-2 |
1 |
12 , -2 |
Четырех точечная аппроксимация второй производной
|
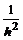 |
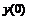
|
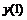
|
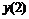
|
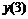
|
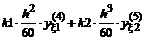
|
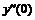
|
2 |
-5 |
4 |
-1 |
55 , -6 |
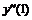
|
1 |
-2 |
1 |
0 |
-5 , -2 |
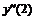
|
0 |
1 |
-2 |
1 |
-5 , -2 |
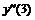
|
-1 |
4 |
-5 |
2 |
55 , -6 |
Пятиточечная аппроксимация второй производной
|
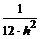 |
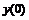
|
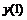
|
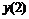
|
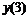
|
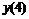
|
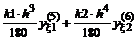
|
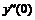
|
35 |
-104 |
114 |
-56 |
11 |
-150 , 12 |
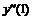
|
11 |
-20 |
6 |
4 |
-1 |
15 , -3 |
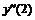
|
-1 |
16 |
-30 |
16 |
-1 |
0 , 2 |
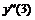
|
-1 |
4 |
6 |
-20 |
11 |
15 , 3 |
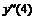
|
11 |
-56 |
114 |
-104 |
35 |
150 , -12 |
Шести точечная аппроксимация второй производной
|
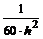 |
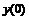
|
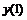
|
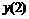
|
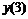
|
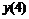
|
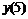
|
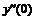
|
225 |
-770 |
1070 |
-780 |
305 |
-50 |
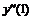
|
50 |
-75 |
-20 |
70 |
-30 |
5 |
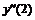
|
-5 |
80 |
-150 |
80 |
-5 |
0 |
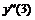
|
0 |
-5 |
80 |
-150 |
80 |
-5 |
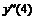
|
5 |
-30 |
70 |
-20 |
-75 |
50 |
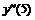
|
-50 |
305 |
-780 |
1070 |
-770 |
225 |
Семи точечная аппроксимация второй производной
|
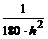 |
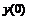
|
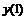
|
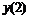
|
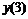
|
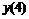
|
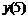
|
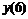
|
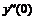
|
812 |
-3132 |
5265 |
-5080 |
2970 |
-972 |
137 |
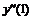
|
137 |
-147 |
-255 |
470 |
-285 |
93 |
-13 |
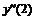
|
-13 |
228 |
-420 |
200 |
15 |
-12 |
2 |
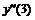
|
2 |
-27 |
270 |
-490 |
270 |
-27 |
2 |
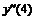
|
2 |
-12 |
15 |
200 |
-420 |
228 |
-13 |
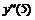
|
-13 |
93 |
-285 |
470 |
-255 |
-147 |
137 |
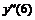
|
137 |
-972 |
2970 |
-5080 |
5265 |
-3132 |
812 |
Например, производная первого порядка 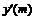 в точках m=0, 3, 5 для семи точечной аппроксимации будет иметь вид:
в точках m=0, 3, 5 для семи точечной аппроксимации будет иметь вид:

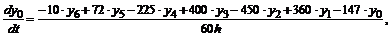
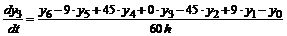 ,
,
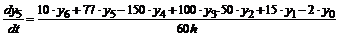 .
.
Аналогично выписываются выражения и для вторых производных в точках 0 и 2:
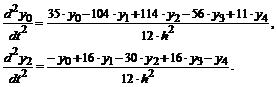
Таким образом, из приведенных таблиц можно выбрать аппроксимирующие выражения для производной в данной точке, включающие значения функции в точках нужного окружения.