Метод простой итерации (последовательного приближения) начинается с неявного разрешения заданной системы алгебраических уравнений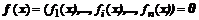 
относительно вектора переменной 
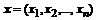, например, так:
,
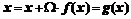где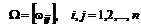 
, матрица масштабирующих коэффициентов, в общем случае недиагональная.
Итерационный процесс начинается с подстановки в правую часть произвольного значения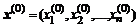 
и вычисления очередного вектора для последующей подстановки:
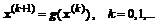
Сходимость к решению такого процесса зависит от вида функции правой части и, следовательно, от величин масштабирующих коэффициентов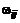 
. Сходимость будет, если скалярная функция 
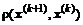, однозначно характеризующая изменение вектора 
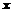за один цикл, больше значения этой функции при подстановке в нее соответствующих 
:
.
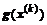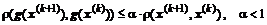Есл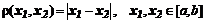и 
и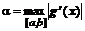 
, условие 
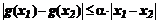именуют условием Липшица.
Если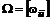 
– диагональная матрица, то величины 
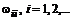можно выбрать из условия отрицательности скорости изменения 
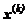. Для этого достаточно взять производную от рекуррентной формулы и установить соответствующее соотношение с нулем:
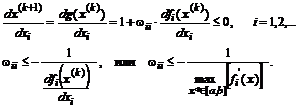
Таким образом, знание максимальных значений производных системы функций в области [a,b]нахождения корня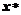 
, позволяет выбрать масштабирующие коэффициенты, обеспечивающие сходимость процесса.
