Возьмем в качестве примера интерполяционный многочлен Ньютона для интерполирования функции “назад”, т.е. в сторону меньших значений независимой переменной по отношению к текущему ее значению:
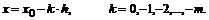
Построение такого интерполяционного многочлена удобно осуществлять с применением повторных конечных разностей “назад”:
.
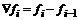Взаимосвязь оператора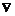 
и рассмотренных выше операторов 
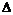и 
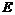характеризуется следующими соотношениями:
Выразим ординату функции, отстоящую от текущей на k шагов назад, через ординату функции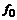 
в текущей точке и выполним ряд эквивалентных преобразований с названными линейными операторами:
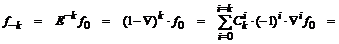
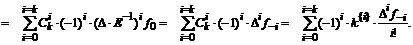
Если положить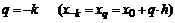 
, то
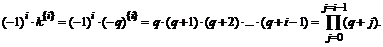
Таким образом, интерполяционный многочлен Ньютона для интерполирования “назад” принимает вид:
,
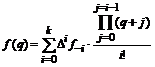где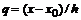 
принимает целые значения для 
,
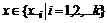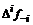– i-тая повторная конечная разность “вперед”, вычисляемая по значениям функции в соответствии с таблицей:
|
|
|
|
|
|
|
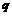
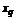
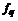
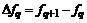
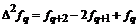
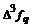
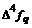
-4 |
|
|
|
|
|
|
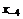
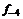
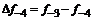
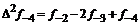
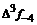
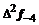
-3 |
|
|
|
|
|
– |
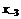
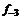
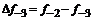
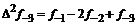
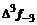
-2 |
|
|
|
|
– |
– |
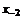
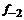
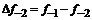
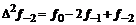
-1 |
|
|
|
– |
– |
– |
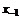
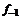
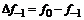
0 |
|
|
|
– |
– |
– |
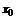
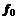
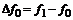
1 |
|
|
|
– |
– |
– |
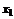
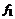
В таблице жирным шрифтом выделены конечные разности от нулевого порядка и выше, которые входят в интерполяционную формулу Ньютона.
