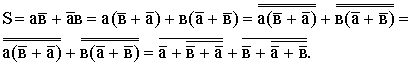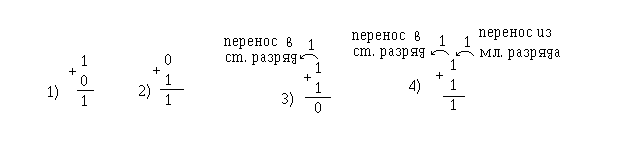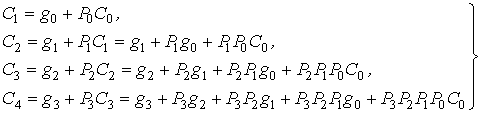Синтез комбинационных сумматоров

Полусумматор это логическая цепь, которая вырабатывает сигналы суммы (S) и переноса (С) при сложении двух двоичных чисел а и в.

Составим таблицу функционирования.

Приведем к виду, удобному для реализации на элементах ИЛИ-НЕ.

.

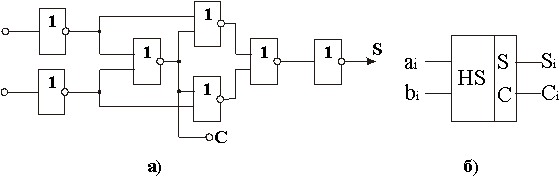
исходя из полученных формул составим схему полусумматора (рис. 2.20, а):

Рис.2.20. Схема полусумматора

Поскольку полусумматор имеет широкое применение и его выпускают в виде отдельной микросхемы, он имеет собственное обозначение (рис. 2.20 б).

Составляя дизъюнктивную нормальную форму для полусумматора, мы получили следующие булевы функции:

 и

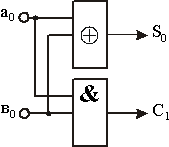
Следовательно, перенос происходит с помощью функции И, а выработка сигнала суммы (функции неравнозначности) производится элементом ИСКЛЮЧАЮЩЕЕ – ИЛИ. На рис.2.21 показана схема полусумматора, составленная из этих элементов.

Рис. 2.21. Схема полусумматора.

Сумматор. В отличие от полусумматора должен воспринимать 3 входных сигнала: 2 слагаемых и сигнал переноса с предыдущего разряда.

Сумматором называется операционный узел ЭВМ, выполняющий операцию арифметического сложения двух чисел.

         Чтобы понять сущность работы комбинационного сумматора, рассмотрим примеры суммирования двух одноразрядных двоичных чисел:

         Из приведенных примеров (1 - 4) видно, что если отсутствует перенос из младшего разряда, то перенос в старший разряд может быть только в одном случае, когда оба числа равны единице. Если же имеется перенос из младшего разряда, то перенос в старший разряд будет всегда, кроме одного случая, когда оба слагаемых равны нулю.

         Составим таблицу функционирования:

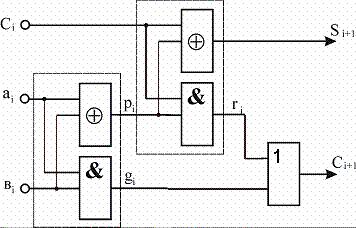
         Схема сумматора может быть реализована на двух полусумматорах, соединенных как указано на схеме рис. 2.22. В этой схеме выделим промежуточные сигналы P_i, g_i, r_i. Введем эти сигналы в новую таблицу функционирования. Соответствие работы этой схемы (рис. 2.22) и таблицы фунционирования можно проверить перебором всех возможных вариантов.

Рис. 2.22. Схема полного сумматора

Многоразрядный сумматор с последовательным переносом. Таким образом, в общем случае для каждого разряда необходима логическая схема с тремя входами a_i, b_i, C_i и двумя выходами S_i, C_i+1. Такая схема и есть полный сумматор. Ее можно реализовать с помощью двух полусумматоров.

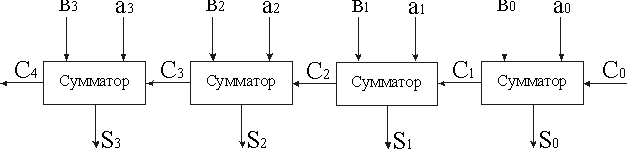
Для сложения двух многоразрядных двоичных чисел на каждый разряд необходим один полный сумматор. Только в младшем разряде можно обойтись полусумматором. На рис. 2.23 приведена схема, предназначенная для сложения двух четырехразрядных чисел А и В. Эта схема выпускается в интегральном исполнении. В ее младшем разряде также используется полный сумматор, чтобы иметь возможность наращивания разрядности схемы.

Рис. 2.23. Сумматор с последовательным переносом

Сумматоры с параллельным переносом. Время выполнения операции в сумматоре с параллельным переносом намного больше времени сложения в одноразрядном сумматоре. Действительно, сигнал переноса С₄ только тогда может принять истинное значение, когда будет установлено правильное значение С₃. Такой порядок выполнения операций называется последовательным переносом (Ripple Carry).

Чтобы уменьшить время операции сложения многоразрядных чисел можно использовать схемы параллельного переноса (Carry look-ahead). При этом все сигналы переноса вычисляются непосредственно по значениям входных переменных.

Согласно таблице переключений, в общем случае для сигнала переноса любого i-го разряда справедливо соотношение:

  .                                     (1)

Величины g_i, r_i вычисляются в качестве промежуточных результатов и в полном сумматоре. Следовательно, их получение не требует дополнительных затрат. Смысл этих величин объясняется совсем просто. Сигнал g_i вырабатывается тогда, когда в данном разряде перенос происходит из-за комбинации входных переменных a_i,b_i. Поэтому его называют функцией генерации переноса. Сигнал P_i показывает, передается ли полученный в младшем разряде сигнал переноса C_i дальше. Поэтому он называется функцией распространения переноса.

Пользуясь выражением (1), можно вывести следующие формулы для вычисления сигналов переноса:  

                 (2)  

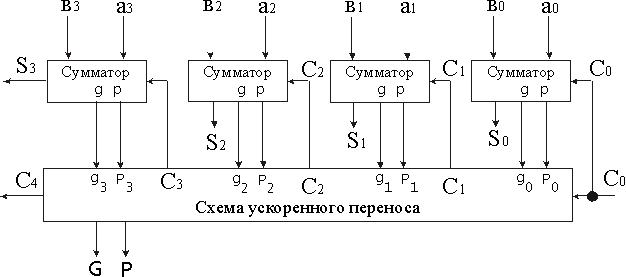
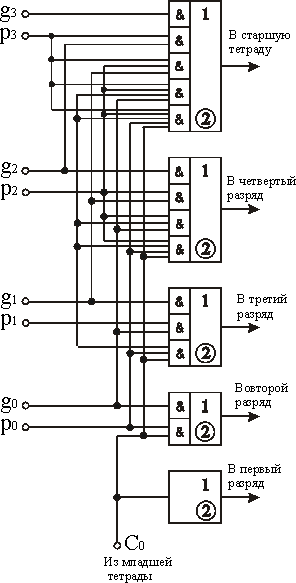
Очевидно, что хотя полученные выражения достаточно сложные, время формирования сигнала переноса в любой разрад с помощью вспомогательных функций определяется только времением здержки распространения сигнала на двух элементах. Эти функции реализуются специальным комбинационным устройством – схемой ускоренного переноса.

Схема сумматора с параллельным переносом приведена на рис. 2.24, а. На рис. 2.24, б изображена схема устройства параллельного переноса в группе из четырех разрядов. Эта схема реализует систему уравнений (2).

Рис. 2.24. Схема сумматора с параллельным переносом

Рис. 2.25. Схема ускоренного переноса

  Схема выпускается в интегральном исполнении.

Сложение чисел, содержащих более четырех разрядов, можно реализовать подключением нескольких четырехразярадных сумматоров.

Вернуться в оглавление:Цифровые автоматы