При интегрировании по методу Симпсона подынтегральная кривая представляется в виде кусочно-непрерывной функцией представляющей отрезки квадратичных парабол, т. е. интерполяционным полиномом 2-й степени (рис. 15.3). При этом интервал (a, b) разбивают на 2n частей с шагом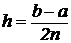 
Формула цифрового интегрирования по методу Симпсона имеет вид:
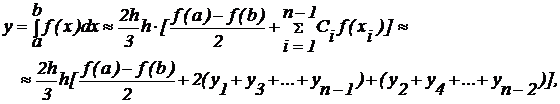
при этом: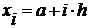 
; 
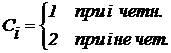
Интегрирование осуществляется путем суммирования элементарных площадей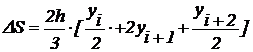 
под кривой подынтегральной функции 
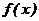на интервале (a, b)
Метод Симпсона обеспечивает большую точность вычисления по сравнению с методом прямоугольников и трапеций.
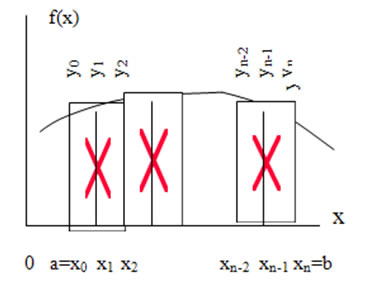
Рис. 14.3. Интегрирование по методу трапеций
