По методу прямоугольников подынтегральная кривая представляется в виде кусочно-линейной функции, отрезки которой параллельны оси абсцисс, т. е. полиномом нулевой степени - константой (рис. 15.1 а, б, в). Промежуток интегрирования [a, b] делится на n равных отрезков, при этом длина каждого отрезка равна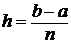 
.
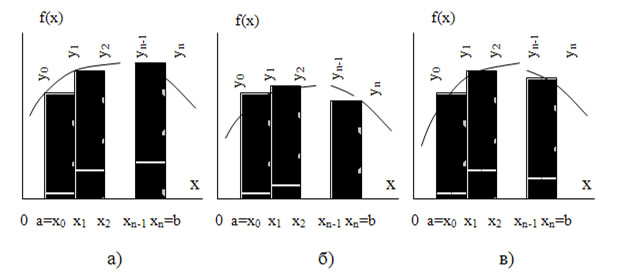
Рис. 14.1. а,б,в. Интегрирование по методу прямоугольников
В зависимости от выбранного метода аппроксимации формулы прямоугольников м.б. представлены в различном виде.
а) Метод левых прямоугольников (рис. 15.1 а) при этом берется значение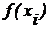 
в начале каждого i–го отрезка
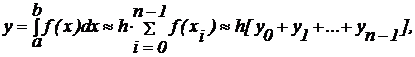
при этом: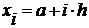 
; 
.
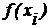б) Метод правых прямоугольников (рис. 15.1 б) при этом берется значение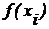 
в конце каждого i–го отрезка
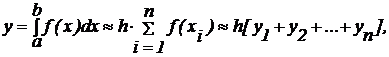
при этом: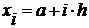 
; 
.
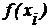в) Метод средних прямоугольников (рис. 15.1 в) при этом берется значение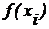 
в средине каждого i–го отрезка
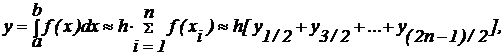
при этом: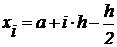 
.
Интегрирование осуществляется путем суммирования элементарных площадей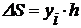 
под кривой подынтегральной функции 
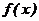на интервале [a, b].
Метод средних прямоугольников обладает более высокой точностью по сравнению с другими методами прямоугольников.
