Методы цифрового интегрирования широко используются в дискретных системах автоматического управления с программной реализацией алгоритмов управления. Методы цифрового интегрирования отличаются в основном способом аппроксимации подынтегральной функции (степенью апросимирующего полинома). Чаще всего используются методы прямоугольников, трапеций и Симпсона, которые содержат минимальное число арифметических операций в алгоритме реализации.
Основу методов цифрового интегрирования составляет геометрический смысл определенного интеграла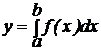 
как площади, ограниченной подынтегральной функцией 
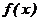, осью абсцисс и ординатам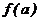и 
и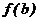 
.
