Задание
К задаче из раздела 2.3 разработать вычислительную модель для получения функции чувствительности решения к точности установки коэффициента b. По найденной временной зависимости этой функции вычислить для 5-10 временных сечений погрешность решения при условии, что погрешность параметра b равна 1%.
Получение и программирование уравнений чувствительности
Возьмем частную производную по b от левой и правой частей системы базовых соотношений, которая получена в результате разложения исходного уравнения в разделе 2.3. При дифференцировании будем учитывать, что все переменные, кроме независимых от b функций времени, зависят и от времени, и от параметра b:
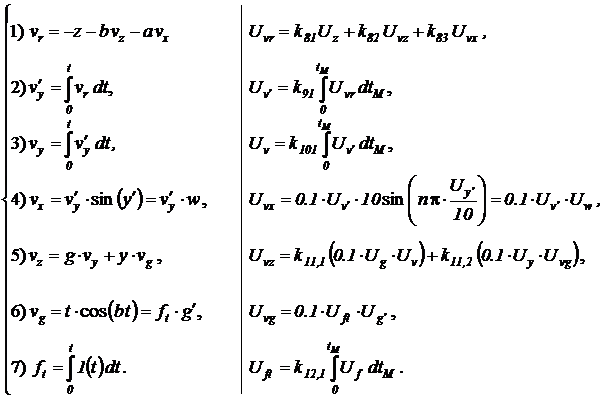
При дифференцировании линейных базовых соотношений по параметру b первые три строки не изменили своей структуры, вызвав лишь замену зависимых переменных 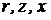 своими функциями чувствительности
своими функциями чувствительности 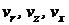 , а внешнюю функцию времени
, а внешнюю функцию времени 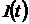 – со знаком минус функцией
– со знаком минус функцией 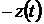 из вычислительной модели исходного уравнения.
из вычислительной модели исходного уравнения.
Дифференцирование нелинейного соотношения четвертой строки дает произведение производной функции чувствительности 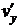 на новую функцию того же аргумента:
на новую функцию того же аргумента: 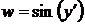 . На структурном уровне это потребует введения двух операционных блоков: функционального преобразования и умножения.
. На структурном уровне это потребует введения двух операционных блоков: функционального преобразования и умножения.
Частная производная пятой строки также потребует введения новых блоков: двух блоков умножения и один сумматор. Дифференцирование шестой строки дает выражение, для которого кроме блока умножения необходимо сгенерировать новую функцию времени 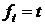 . Определяющим дифференциальным уравнением этой функции будет уравнение следующего вида:
. Определяющим дифференциальным уравнением этой функции будет уравнение следующего вида:
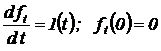 .
.
Для решения такого уравнения требуется интегратор, на вход которого поступает единичная функция времени.
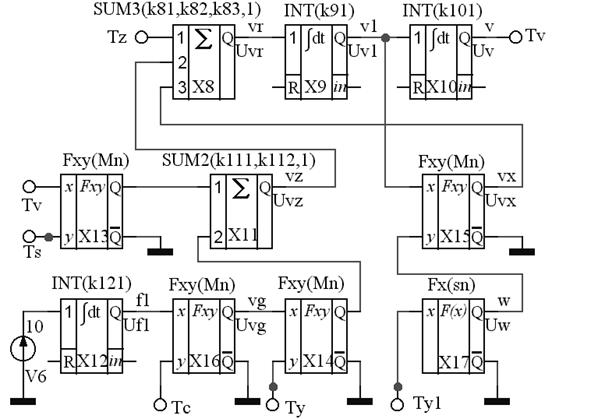
Функции 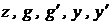 в схему вычислительной модели должны вводиться из вычислительной модели исходного уравнения. Схема соединения операционных блоков для вычисления функций чувствительности приведена на рисунке 57.
в схему вычислительной модели должны вводиться из вычислительной модели исходного уравнения. Схема соединения операционных блоков для вычисления функций чувствительности приведена на рисунке 57.
Рисунок 57
Справа от системы базовых соотношений с функциями чувствительности представлена соответствующая ей система с машинными переменными.
Между функциями чувствительности и представляющими их напряжениями необходимо ввести масштабные множители. Масштабные множители переменных, которые вводятся из вычислительной модели уравнения в вычислительную модель функции чувствительности, используются без изменения.
Уже известными масштабными множителями являются:
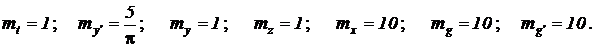
Масштабные множители для функции чувствительности и ее производной выберем одинаковыми и равными
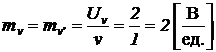 .
.
Дополнительный перечень новых масштабных соотношений выписан справа.
Для функции 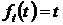 при длительности наблюдения решений в одну секунду масштабный множитель вычислим так
при длительности наблюдения решений в одну секунду масштабный множитель вычислим так
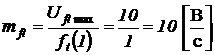 .
.
Остальные масштабные множители рассчитаем или выберем в процессе установления подобия между уравнениями чувствительности и соотношениями ее вычислительной модели.
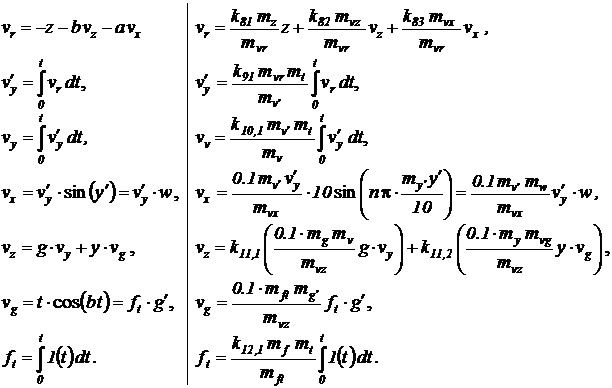
Приравнивая коэффициенты, стоящие при одинаковых группах переменных, получим следующую систему уравнений для параметров операционных блоков и масштабных множителей:
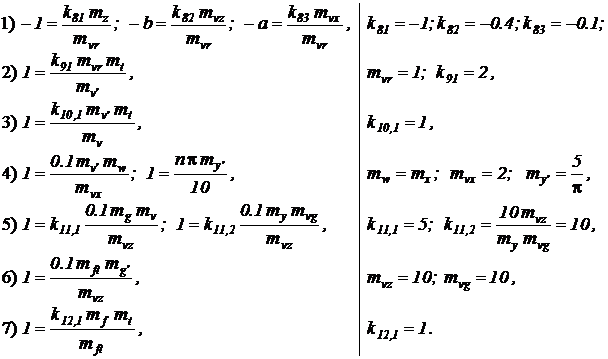
Последовательный расчет или выбор коэффициентов передач и масштабных множителей проводился здесь снизу вверх.
Начальные условия всех интеграторов в вычислительной модели уравнений чувствительности равны нулю по определению.
Корректность вычисления функций чувствительности оценим по результатам совместной работы одновременно следующих трех вычислительных моделей: вычислительных моделей исходного уравнения с точно и неточно установленным значением коэффициента b и вычислительной модели уравнений чувствительности. Коэффициентам передач по входам операционных блоков, которые определяются коэффициентом b , в вычислительной модели возмущенного уравнения дадим значения, например, на 1% меньше номинальных. На полной схеме, содержащей все три вычислительные модели и показанной на рисунке 58, этими коэффициентами являются q12= -3,96, q61= -3,96 и q71= 3,96 (вместо 4).
Проверку количественных соотношений погрешности функции 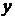 и ее производной
и ее производной 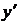 выполним двумя методами:
выполним двумя методами:
- традиционным методом -
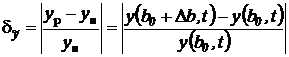 и
и
- по функциям чувствительности -
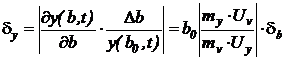 ,
,
где 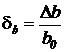 - относительная погрешность параметра b, равная 0,01;
- относительная погрешность параметра b, равная 0,01;
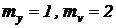 - масштабные множители, связывающие реальные и машинные переменные;
- масштабные множители, связывающие реальные и машинные переменные;
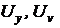 - машинные переменные, представляющие решение и функцию чувствительности.
- машинные переменные, представляющие решение и функцию чувствительности.
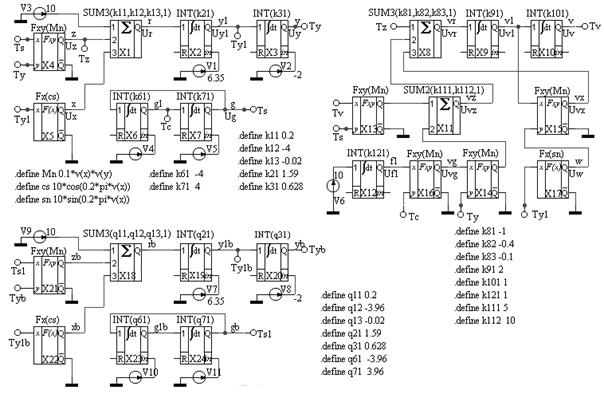
Рисунок 58
Для вычисления относительной погрешности необходимо регистрировать, по крайней мере три процесса: функцию возмущенного решения 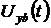 , функцию чувствительности решения
, функцию чувствительности решения 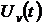 и функцию идеального
и функцию идеального 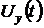 (невозмущенного) решения. Так как относительная погрешность является функцией времени, то к трем процессам добавим еще два: кривые погрешности, вычисляемые по традиционной методике и по функциям чувствительности. Графики погрешностей для их нормального представления в десяти вольтовой шкале напряжений умножим на 103.
(невозмущенного) решения. Так как относительная погрешность является функцией времени, то к трем процессам добавим еще два: кривые погрешности, вычисляемые по традиционной методике и по функциям чувствительности. Графики погрешностей для их нормального представления в десяти вольтовой шкале напряжений умножим на 103.
На рисунке 59 приведены графики, позволяющие оценить погрешность решения исходного уравнения, а на рисунке 60 графики, позволяющие оценить погрешность производной решения. Числовые значения изображенных процессов в одиннадцати временных сечениях представлены в таблице 7.
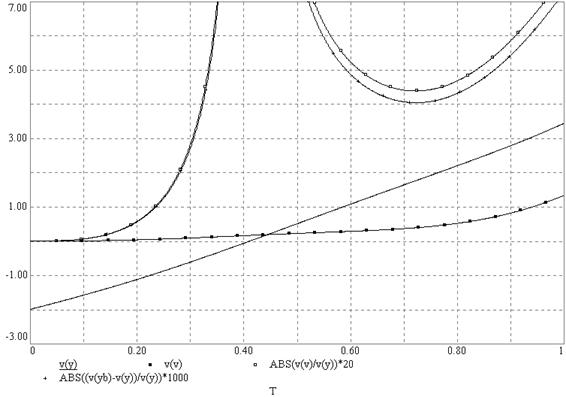
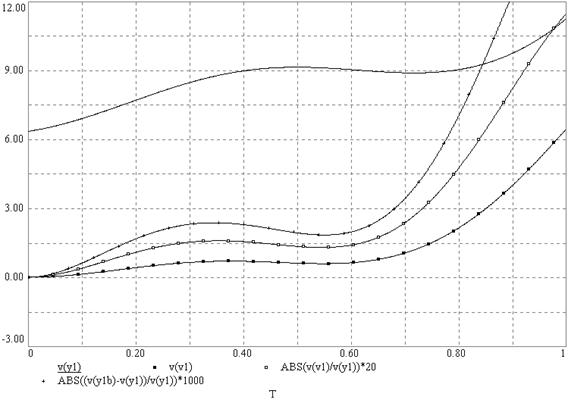
Рисунок 59
Рисунок 60
Таблица 7. – Числовые значения кривых в вольтах.
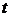
|
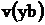
|
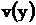
|
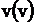
|
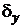
|
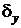
|
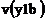
|
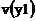
|
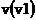
|
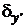
|
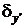
|
0.0000 |
-2.0000 |
-2.0000 |
0.0000 |
0.00 |
0.00 |
6.3499 |
6.3499 |
0.0000 |
0.00 |
0.00 |
0.1000 |
-1.5860 |
-1.5859 |
0.0047 |
0.06 |
0.06 |
6.8976 |
6.9019 |
0.1353 |
0.39 |
0.61 |
0.2000 |
-1.1285 |
-1.1279 |
0.0320 |
0.57 |
0.55 |
7.6887 |
7.7015 |
0.4174 |
1.08 |
1.67 |
0.3000 |
-0.6210 |
-0.6193 |
0.0863 |
2.79 |
2.69 |
8.4492 |
8.4687 |
0.6460 |
1.53 |
2.30 |
0.4000 |
-0.0727 |
-0.0697 |
0.1550 |
44.54 |
42.41 |
8.9579 |
8.9785 |
0.6957 |
1.55 |
2.29 |
0.5000 |
0.4968 |
0.5010 |
0.2209 |
8.82 |
8.31 |
9.1227 |
9.1404 |
0.6148 |
1.35 |
1.93 |
0.6000 |
1.0674 |
1.0726 |
0.2811 |
5.24 |
4.88 |
9.0187 |
9.0364 |
0.6300 |
1.39 |
1.97 |
0.7000 |
1.6285 |
1.6352 |
0.3605 |
4.41 |
4.07 |
8.8679 |
8.8982 |
1.0497 |
2.36 |
3.40 |
0.8000 |
2.1865 |
2.1959 |
0.5133 |
4.68 |
4.31 |
8.9693 |
9.0323 |
2.1324 |
4.72 |
6.98 |
0.9000 |
2.7665 |
2.7816 |
0.8126 |
5.84 |
5.42 |
9.6152 |
9.7347 |
3.9766 |
8.17 |
12.27 |
1.0000 |
3.4104 |
3.4353 |
1.3293 |
7.74 |
7.26 |
11.0341 |
11.2324 |
6.4285 |
11.45 |
17.66 |
В таблице первая колонка представляет моменты времени. Колонки 2-6 представляют временные сечения кривых рисунка 59, а колонки 7-11 – временные сечения кривых рисунка 60. Относительные погрешности, помещенные в таблицу и изображенные на кривых, вычислялись по формулам:
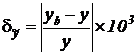 ,
,
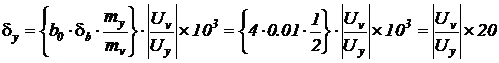 .
.
Разделив табличное значение напряжения на 1000, мы получим значение относительной погрешности. Например, при t=0,7 с погрешность решения составляет примерно 0,4% (0,00441 и 0,00407).
Нетрудно видеть, что метод, основанный на функциях чувствительности, позволяет с предельно высокой точностью оценивать погрешность решения задачи, вызванной неточностью установки в вычислительной модели параметров операционных блоков.
На рисунке 59 имеются в решении такие области, где относительная погрешность резко возрастает, хотя абсолютная погрешность имеет конечную монотонно изменяющуюся величину.

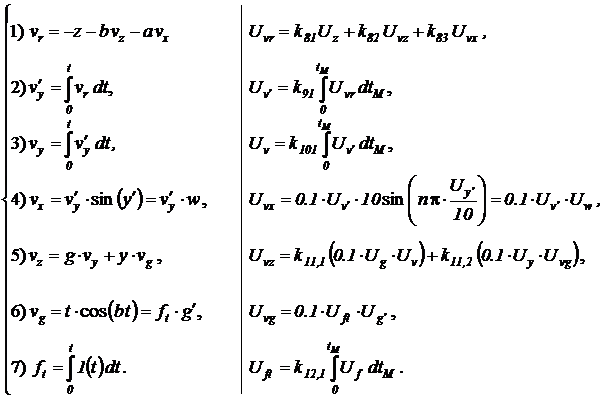
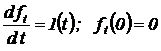 .
.
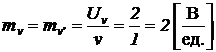 .
.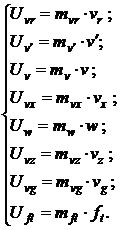
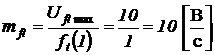 .
.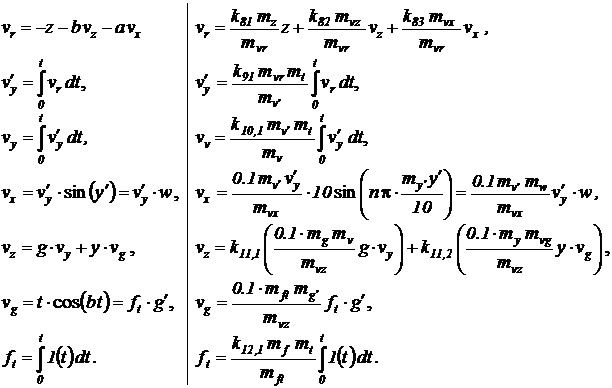
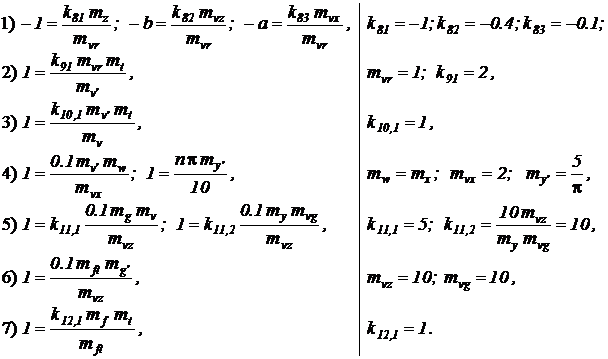
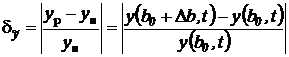 и
и 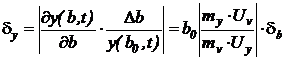 ,
,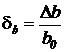 - относительная погрешность параметра b, равная 0,01;
- относительная погрешность параметра b, равная 0,01;


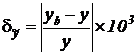 ,
,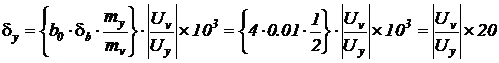 .
.