Задание
Принимая во внимание, что в состав аналоговой вычислительной машины (АВМ) с десяти вольтовым диапазоном изменения переменных, кроме линейных операционных блоков, имеются нелинейные блоки со следующими соотношениями вход-выход:
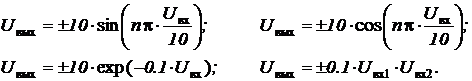
Выполнить все этапы программирования и решить следующее нелинейное дифференциальное уравнение №# из п.4.1.3.
Расчетные соотношения для параметров вычислительной модели получить сначала в формульном виде. Численные значения исходных данных взять из таблицы задания.
|
№ |
Уравнение |
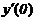
|
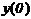
|
a |
b |
c |
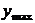
|
# |
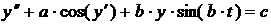
|
4 |
-2 |
0.2 |
4 |
2 |
5 |
Программирование задачи
Представим исходное уравнение системой соотношений между основными и промежуточными переменными, для которых имеются операционные блоки. Для каждого блока выпишем выражение между входными и выходными машинными переменными и введем масштабные соотношения между реальными и машинными переменными:
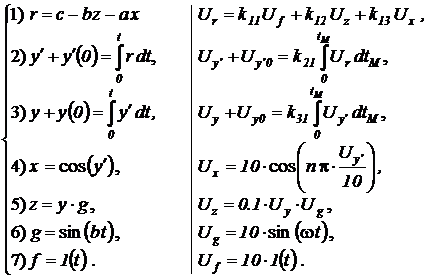
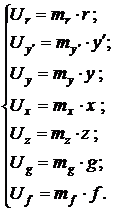
Для воспроизведения синусоидальной функции времени 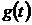 найдем определяющее дифференциальное уравнения, решением которого будет синус. Дважды дифференцируя
найдем определяющее дифференциальное уравнения, решением которого будет синус. Дважды дифференцируя 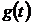 по времени и исключая явную зависимость производных от функций времени, получим нужное уравнение и вычислим начальные условия при
по времени и исключая явную зависимость производных от функций времени, получим нужное уравнение и вычислим начальные условия при 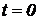 :
:
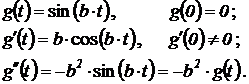
Начальные условия определяют амплитуду и фазу генерируемых функций синуса и косинуса с угловой частотой b. Для получения единичных амплитуд при нулевом фазовом сдвиге уравнение необходимо решать со следующими начальными условиями:
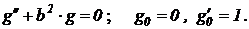
Представим и это дифференциальное уравнение системой базовых соотношений, воспроизводимых операционными блоками:
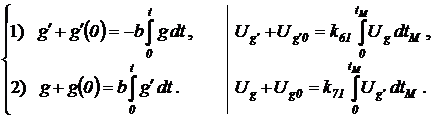
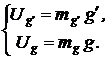
Схемы соединения операционных блоков для системы операторных соотношений исходного уравнения и генерирования синусоиды приведены на рисунке 55.
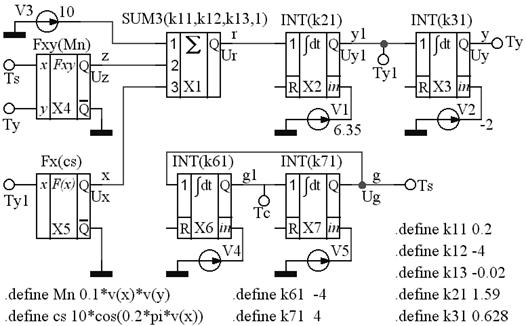
Рисунок 55
|
Для установления подобия двух систем базовых соотношений заменим в машинной системе машинные переменные реальными, используя масштабные соотношения, и приравняем постоянные коэффициенты при одинаковых переменных двух систем.
Влиять на скорость развертки процессов решения можно выбором масштаба времени, который связывает реальное время t с машинным временем tM следующим образом: 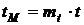 .
.
После замены, разделив левые и правые части уравнений на масштабные множители, стоящие в левых частях соотношений, и приравняв после этого постоянные коэффициенты при одноименных переменных в системах с реальными и машинными переменными, получим систему уравнений, связывающую все параметры схемы и масштабные множители.
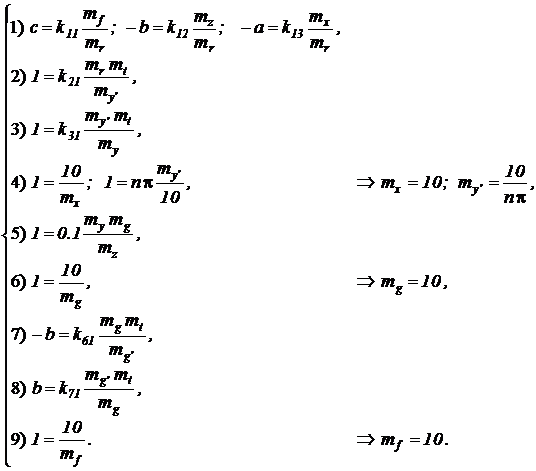
Для нахождения численных значений параметров операционных блоков, обозначенных в этой системе как 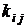 , где индексы i и j определяют соответственно номер блока и номер входа, необходимо сначала задать или вычислить значения масштабных множителей для переменных.
, где индексы i и j определяют соответственно номер блока и номер входа, необходимо сначала задать или вычислить значения масштабных множителей для переменных.
В первую очередь найдем предопределенные нелинейными блоками и генераторами функций времени масштабные множители, полагая 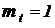 . Значения этих масштабных множителей показаны в приведенной выше системе соотношений справа.
. Значения этих масштабных множителей показаны в приведенной выше системе соотношений справа.
Зная из задания ориентировочное значение 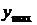 , вычисляем для него с некоторым запасом
, вычисляем для него с некоторым запасом 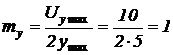 .
.
Из 5-го соотношения: 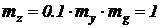 .
.
Выбрав для функций времени синуса и косинуса одинаковые масштабы 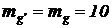 , вычисляем по соотношениям 7 и 8:
, вычисляем по соотношениям 7 и 8:
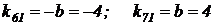 .
.
Из 3-й строки: 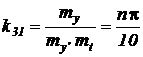 .
.
Здесь параметр нелинейного блока n определяет диапазон изменения аргумента в радианах при изменении входной переменной от нуля до 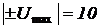 В. Возьмем n=2, тогда
В. Возьмем n=2, тогда 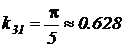 .
.
Для дальнейших вычислений необходимо знать либо масштаб суммы 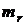 , либо коэффициент
, либо коэффициент 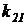 , так как
, так как 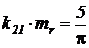 . Масштаб суммы входит делителем во все соотношения первой строки, в числителе которых стоят масштабные множители
. Масштаб суммы входит делителем во все соотношения первой строки, в числителе которых стоят масштабные множители 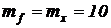 и
и 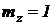 . Поэтому разумно выбрать
. Поэтому разумно выбрать 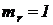 , чтобы все коэффициенты оказались вокруг порядка единицы. Тогда
, чтобы все коэффициенты оказались вокруг порядка единицы. Тогда
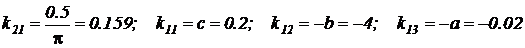 .
.
Вычислим напряжения начальных условий для интеграторов исходного уравнения
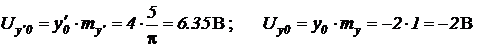
и генератора синусоиды
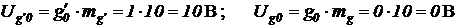 .
.
Решение уравнения выполним в течение одной секунды. На этом интервале синусоидальная функция времени изменит знак у слагаемого с переменной y на противоположный, что должно качественно изменить вид решения, так как корни характеристического уравнения в уравнении второго порядка становятся положительными и означают неограниченное возрастание амплитуды решения. На рисунке 56 приведены результаты моделирования. Изменения всех переменных представлены графиками, для которых проводился ориентировочный расчет масштабных множителей. Все кривые практически не выходят за пределы десяти вольтового диапазона изменения машинных переменных. Это значит, что все предположения о максимальных значениях реальных переменных сделаны корректно.
|
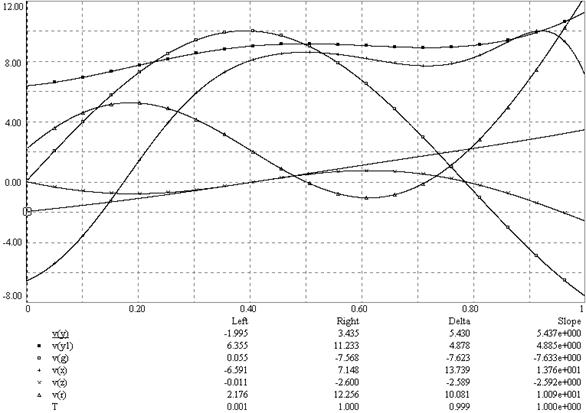
Рисунок 56
|
Полученные кривые после t=0.8 c, где переменная g(t) становится отрицательной, действительно демонстрируют существенное увеличение амплитуд.

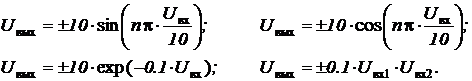
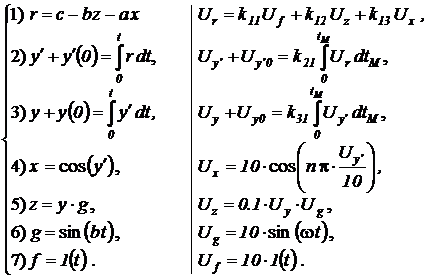
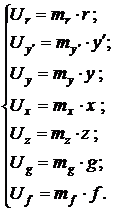
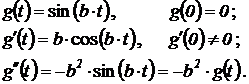
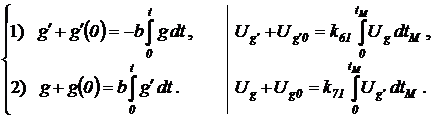
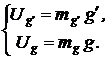

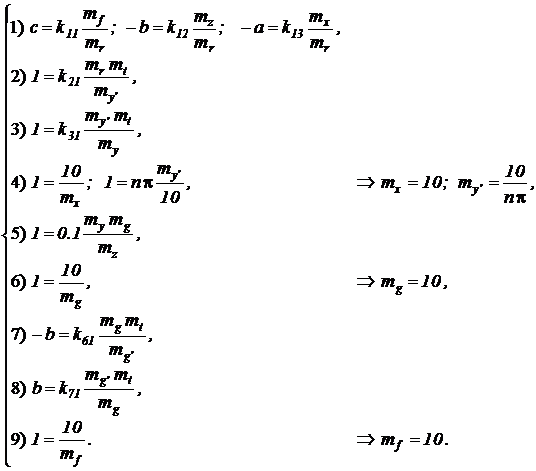
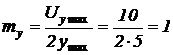 .
.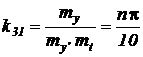 .
.