Задание
Выполнить расчет и провести лабораторные исследования линейного операционного блока методом схемотехнического моделирования, при этом необходимо:
|
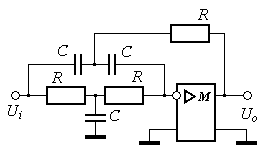
Рисунок 44 |
Получить соотношение между входным и выходным напряжениями операционного блока в символьном виде, полагая коэффициент усиления усилителя равным бесконечности. Схема приведена на рисунке 44.
При получении численных значений использовать произведение величин сопротивления и емкости равное единицы.
Путем прямого моделирования электрической схемы подтвердить правильность результатов расчета.
Вывод соотношения
Входная цепь идеального операционного усилителя с отрицательной обратной связью для внешней схемы является коротким замыканием по напряжению и разрывом для тока. Это позволяет считать входное сопротивление между входными клеммами усилителя равным бесконечности. Входное напряжение приравнивать либо к нулю, полагая коэффициент усиления усилителя равным бесконечности, либо к 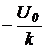 - при конечном коэффициенте усиления, равном k. Выполним ряд эквивалентных преобразований внешней схемы усилителя.
- при конечном коэффициенте усиления, равном k. Выполним ряд эквивалентных преобразований внешней схемы усилителя.
Обведенную пунктиром часть схемы рисунка 45 преобразуем в эквивалентную схему последовательно включенных источника ЭДС с напряжением холостого хода  и его внутреннего сопротивления
и его внутреннего сопротивления 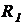 , которые соответственно равны:
, которые соответственно равны:
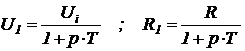 ,
,
где 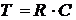 - постоянная времени.
- постоянная времени.
|
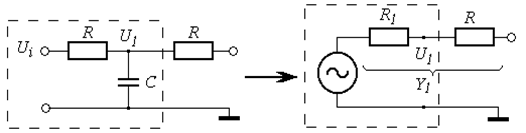
Рисунок 45
Эквивалентное преобразование интегрирующей цепочки. |
Внутреннее сопротивление 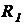 и внешнее сопротивление R образуют общее сопротивление с проводимостью
и внешнее сопротивление R образуют общее сопротивление с проводимостью
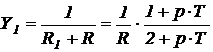 .
.
Аналогично выполним эквивалентное преобразование суммиру-ющего участка внешней схемы усилителя, показанной на рисунке 46.
Рисунок 46
Эквивалентное преобразование суммирующей цепочки.
Напряжение холостого хода 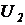 суммирующей цепи, выделенной пунктирным контуром, и ее внутреннее сопротивление
суммирующей цепи, выделенной пунктирным контуром, и ее внутреннее сопротивление 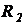 имеют следующие выражения:
имеют следующие выражения:
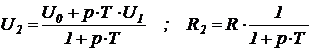 .
.
В результате последовательная эквивалентная проводимость схемы рисунка 46 равна
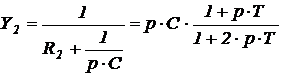 .
.
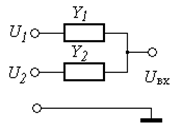
Теперь напряжение  на входе усилителя определяется суммирующей схемой, представленной на рисунке 47.
на входе усилителя определяется суммирующей схемой, представленной на рисунке 47.
Рисунок 47
Операторное выражение для входного напряжения запишем так:
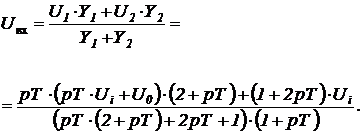
Так как в задании рекомендуется использовать усилитель с бесконечно большим коэффициентом усиления, то это выражение для 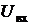 приравняем нулю и разрешим полученное уравнение относительно напряжения на выходе усилителя
приравняем нулю и разрешим полученное уравнение относительно напряжения на выходе усилителя 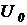 :
:
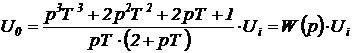 .
.
Чтобы убедиться в правильности полученного выражения, рассмотрим реакцию схемы на стандартное входное воздействие. В качестве последнего, учитывая дифференцирующие свойства передаточной функции (степень полинома в числителе больше степени полинома знаменателя), возьмем линейно возрастающее напряжение 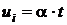 . В преобразованном по Лапласу виде такое входное воздействие записывается так:
. В преобразованном по Лапласу виде такое входное воздействие записывается так: 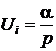 .
.
Взяв значение постоянной времени 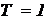 и
и 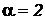 , получим для заданной схемы следующее изображение выходного напряжения в области комплексной переменной:
, получим для заданной схемы следующее изображение выходного напряжения в области комплексной переменной:
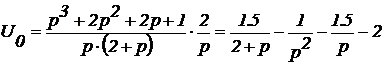 .
.
По таблицам обратного преобразования Лапласа для каждого слагаемого находим оригинал. Их алгебраическая сумма даст общее выражение для выходного напряжения во временной области:
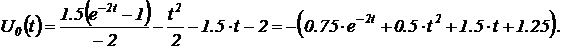
Чтобы позднее сопоставить результаты вывода с результатами предстоящего лабораторного исследования заданной схемы, вычислим значение переходного процесса в точке 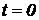 и
и  секунд:
секунд:
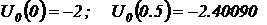 .
.
Моделирование схемы
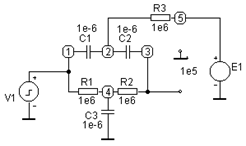
Моделирование схемы выполним в среде пакета Micro-Cap V. Вычислительная модель схемы с операционным усилителем, имеющим коэффициент усиления 100000, показана на рисунке 48.
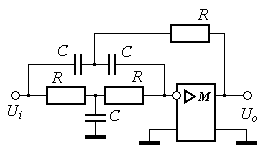
Рисунок 48
На схеме операционный усилитель представлен источником напряжения, который управляется напряжением. Коэффициент усиления его равен 105. Сопротивления R1...R3 и конденсаторы С1...С3 равны соответственно 106 Ом и 10-6 Ф. Их произведение равно одной секунде. Цифры в кружках являются маркировкой узлов и служат для идентификации напряжений и токов в моделируемой схеме.
График переходного процесса представлен на рисунке 49.
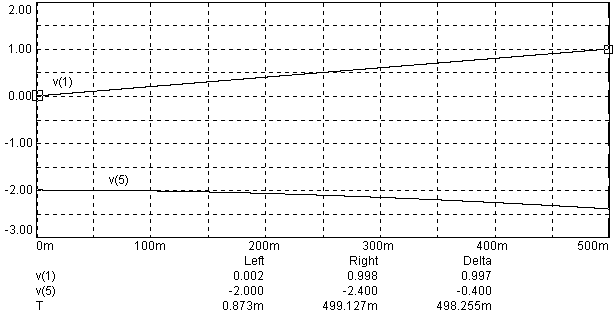
Рисунок 49.
Переходный процесс воспроизведен до точки t=0.5 c. В нижней части графиков приведены значения кривых v(1) и v(5) в крайних слева и справа сечениях. Из этих сечений видно, что входное воздействие начинается с нуля и изменяется по прямой линии с угловым коэффициентом равным 2, а выходная реакция при t=0 c претерпевает скачок на уровень –2 В и при t=0.5 c достигает значения –2.4 В. Оба результата совпадают с аналитически полученными значениями в расчетной части работы, что подтверждает правильность полученного аналитического выражения, связывающего выходное напряжение со входным в заданной схеме операционного блока.


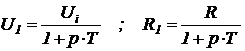 ,
,
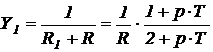 .
.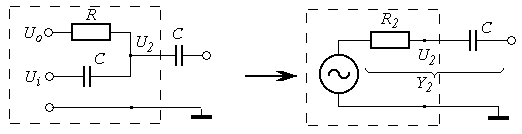
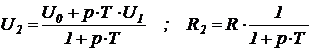 .
.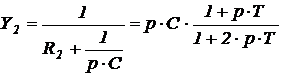 .
.
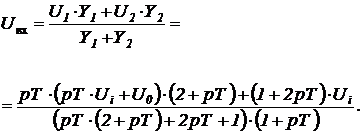
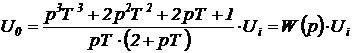 .
.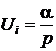 .
.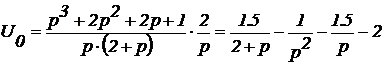 .
.