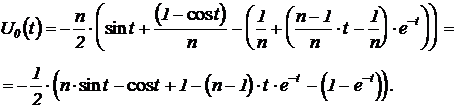Реакция операционного блока на входные воздействия

Всякий аналитический расчет передаточной функции операционного блока требует проверочных действий на его безошибочность. Лучшей проверкой можно считать ту, которая двумя различными методами обеспечивает получение одинаковых конечных результатов в заданном диапазоне изменения входных переменных. В рассматриваемом случае к таким исследованиям передаточной функции можно отнести аналитический расчет реакции блока на известный входной сигнал и схемотехническое моделирование работы устройства с тем же входным воздействием.

В качестве пробного воздействия на устройство выбирают такой сигнал, который в реальном устройстве обеспечивал бы физически реализуемую реакцию, а точнее - исключал бы на выходе формирование сигнала бесконечно большой амплитуды.

По виду дробно-рациональной функции несложно определить требования к входному сигналу, вернее, - к его преобразованному по Лапласу виду: степень полинома от комплексной переменной в числителе после умножения передаточной функции на изображение по Лапласу входного сигнала должна оказаться меньше степени полинома знаменателя.

Наиболее удобным способом преобразования операторного выражения выходной реакции операционного блока в область действительной (временной) переменной является табличный. В приложении (п. 5.1) приведена таблица наиболее важных соответствий между аналитическими и временными функциями. Операторные функции, приведенные здесь, отличаются от преобразованных по Лапласу лишь комплексным множителем p. Это дает право считать их комплексными представлениями переходных характеристик, временные функции которых приведены в правой колонке. И обратно, учитывая наличие комплексного множителя, произведение передаточной функции и оператора входного воздействия будет представлять комплексное выражение для выходной реакции. Поэтому, найдя в левой колонке аналогичное операторное выражение, в правой колонке прочитываем закон изменения выходной величины во времени.

При равенстве степеней числителя и знаменателя в реакции на выходе должна наблюдаться составляющая, пропорциональная входному сигналу, при отличии на единицу и более реакция может включать в функциональном сочетании временную, апериодическую или периодическую компоненты.

Если полученной дробно-рациональной функции в таблице нет, то благодаря линейности интегрального преобразования ее можно разложить на сумму слагаемых, которые в таблице присутствуют. Основная сложность этого этапа в том, чтобы определить состав и вид слагаемых. Этот состав определяется путем разложения знаменателя передаточной функции на сомножители вида:

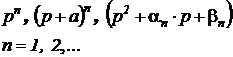
В свою очередь третье выражение при известных 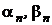 сводится к знаменателю табличного вида:

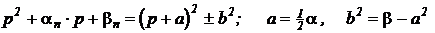
Выражения третьего вида появляются тогда, когда в знаменателе имеются пары комплексно сопряженных корней. Когда определены сомножители, общую сумму слагаемых можно представить так:

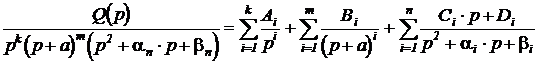
Неизвестные коэффициенты 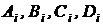 находятся из уравнений, получаемых путем приравнивания двух полиномов: полинома числителя левой дроби  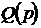и полинома числителя правой дроби, получаемой после приведения к общему знаменателю. Достижение равенства возможно, если постоянные коэффициенты при слагаемых с одинаковыми степенями p равны.

Для каждого из присутствующих слагаемых в таблице можно найти оригинал. Например, слагаемые второй суммы сводятся к виду слагаемых №3 и №23 путем умножения числителя и знаменателя на p и замены комплексной переменной :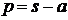

.

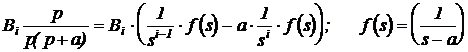Слагаемые третьей суммы приводятся к табличным следующим образом:

;

.

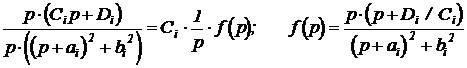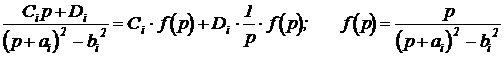В более сложных случаях используют специальные справочники.

В качестве примера обратного преобразования используем передаточную функцию третьего примера из пункта 1.1.3.

Для единичного скачка на входе 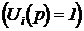 операторное выражение реакции на выходе будет иметь табличный вид (№13) с параметрами 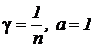, для которого временное представление переходной характеристики будет записано так:

.

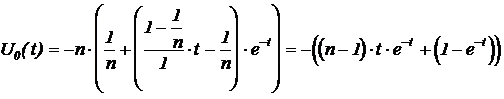Если в качестве входного взять синусоидальное воздействие:

 ,

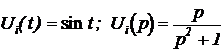то операторное выражение реакции на выходе будет иметь такой вид:

.

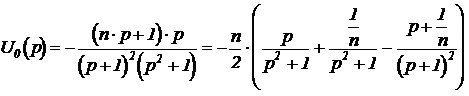Первое, второе и третье слагаемые в скобках имеют табличные выражения, стоящие под номерами соответственно 6, 5 и 13. Таким образом

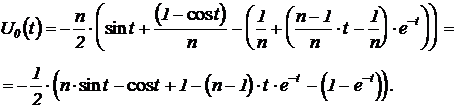
В математическом пакете DERIVE разложение на простые дробно-рациональные слагаемые и их частичные приведения к общему знаменателю выполняются по командам Expand и Factor.

Численный расчет можно выполнить и в среде моделирующего пакета Micro-CapV. Здесь возможны два варианта воспроизведения переходных процессов: обычным схемотехническим моделированием устройства в базисе электрических компонент и непосредственно заданием передаточной функции управляемому источнику напряжения или тока.
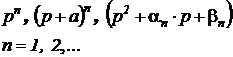
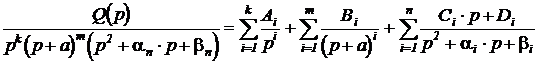
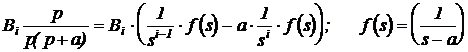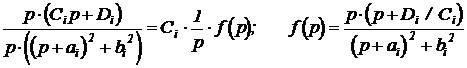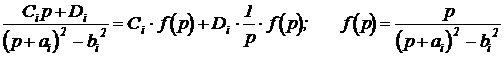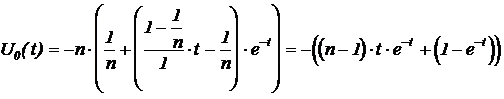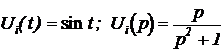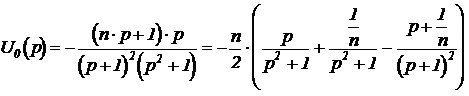