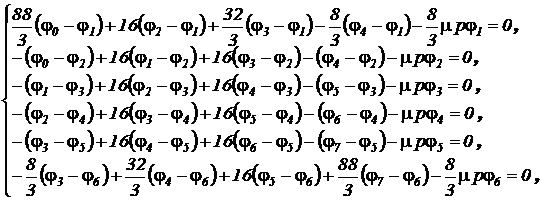В качестве примеров построения структур вычислительных моделей краевых задач в обыкновенных и частных производных возьмем следующие уравнения:
- неоднородное линейное дифференциальное уравнение
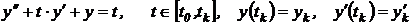 ;
;
- однородное линейное дифференциальное уравнение
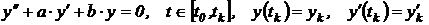 ;
;
- однородное дифференциальное уравнение теплопроводности
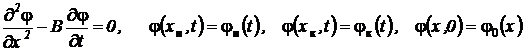 .
.
Вариант схемы соединения операционных блоков для решения неоднородного линейного дифференциального уравнения методом сведения к задаче Коши приведен на рисунке 41.
|
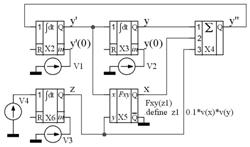
Рисунок 41 |
На схеме блоки Х2, Х3, Х4, Х5 воспроизводят однородную часть линейного уравнения, а блок Х6 с источником V4 реализует функцию z пропорциональную времени. Источник V3 устанавливает начальное значение для z(t). Блок Х5 определен как устройство умножения. Источники V1, V2 устанавливают начальные значения.
Для этой структуры нужное частное решение уравнения с правой частью будет получено, если значения напряжений на источниках V1, V2 взять равные нулю. Для получения частных решений однородного уравнения правую часть его нужно отключить, сделав коэффициент передачи сумматора по третьему входу нулевым, и устанавливать на источниках V1, V2 требуемые значения напряжений. Конечные значения всех частных решений необходимо запоминать для дальнейшего расчета начальных условий, обеспечивающих решение краевой задачи.
Схема решения краевой задачи в обыкновенных производных, использующая итерационный подбор одновременно двух начальных условий по методу Ньютона, приведена на рисунке 42.
|
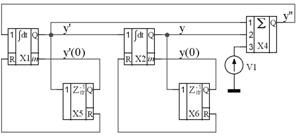
Рисунок 42 |
В данном примере блоки Х1, Х2, Х4 образуют структуру вычислительной модели для решения дифференциального уравнения второго порядка.
Блоки Х5, Х6 служат для вычисления начальных условий методом Ньютона, (п.1.7.2), которые устанавливаются перед очередным решением.
Начало очередного решения определяется импульсами сброса интеграторов в ноль по входам R, вырабатываемыми блоками 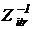 в момент выдачи новых значений начальных условий. Параметрами итерационных блоков служат: конечное значение входной переменной, предварительное значение начального условия и заданное время решения дифференциального уравнения
в момент выдачи новых значений начальных условий. Параметрами итерационных блоков служат: конечное значение входной переменной, предварительное значение начального условия и заданное время решения дифференциального уравнения 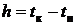 . При удачном выборе исходных начальных условий число итераций составляет не менее 3–5, умноженное на число приближаемых параметров.
. При удачном выборе исходных начальных условий число итераций составляет не менее 3–5, умноженное на число приближаемых параметров.
Для многомерных нелинейных дифференциальных уравнений рассмотренные итераторы практически малопригодны. Эффективно работающие итерационные процедуры Ньютона требуют вычисления определителей с частными производными, вычисляемыми на каждом шаге итерации, и удачного выбора начальных условий, находящихся около искомых значений.
Для уравнения теплопроводности разделим область решения 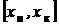 на 7 равных частей. Граничные точки
на 7 равных частей. Граничные точки 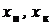 охватывают точки с неизвестными значениями потенциалов
охватывают точки с неизвестными значениями потенциалов 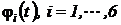 . Значения
. Значения 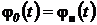 и
и 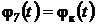 являются заданными функциями на границе.
являются заданными функциями на границе.
Пятиточечная аппроксимация второй производной по x, взятая из таблицы 4, после подстановки в уравнение теплопроводности для каждой внутренней точки области решения порождает систему дифференциальных уравнений первого порядка следующего вида:
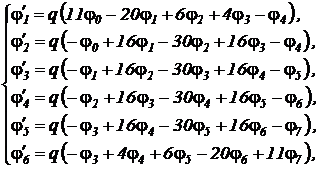 или
или 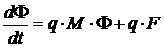
где 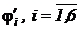 - производные от потенциала по времени;
- производные от потенциала по времени;
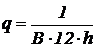 - коэффициент,
- коэффициент,
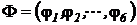 - вектор искомых потенциалов,
- вектор искомых потенциалов,
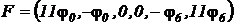 - вектор внешних воздействий.
- вектор внешних воздействий.
На рисунке 42 внешние воздействия представлены источниками V1,V2. Начальное распределение потенциала задается источниками V3-V8.
|
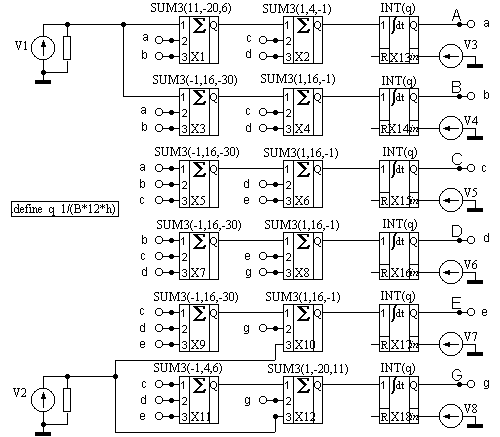
Рисунок 43 |
В векторном представлении системы дифференциальных уравнений матрица коэффициентов размером 6x6 имеет следующий вид:
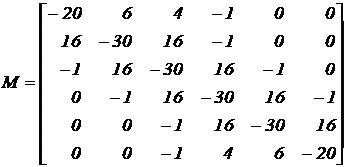 .
.
Конечно-разностную систему уравнений, сформированную из исходного дифференциального уравнения в частных производных, можно решить, используя метод физической аналогии. В качестве физического аналога выбирают звездообразную электрическую цепь, состоящую из линейных электрических компонент. Зависимость между токами и напряжениями в такой цепи (рисунок 1) в преобразованном по Лапласу виде описывается законами Ома и Кирхгофа:
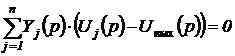 .
.
В аналогичной форме можно переписать и конечно-разностную систему уравнений:
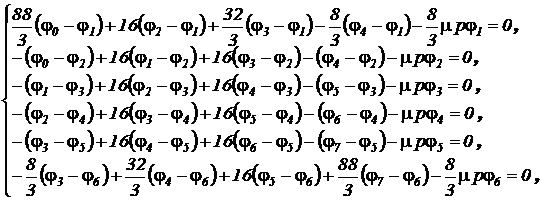
где 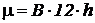 .
.
Установив взаимно однозначное соответствие между значением потенциала в уравнении и электрическим напряжением в электрической цепи посредством масштабного соотношения 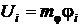 , после замены переменных каждая строка уравнения будет представлять электрический аналог с четырьмя резисторами и одним конденсатором. Коэффициенты перед скобками определяют величину проводимости, подключаемую между вычитаемыми напряжениями. Коэффициент при слагаемом, представляющем производную, после введения масштаба времени
, после замены переменных каждая строка уравнения будет представлять электрический аналог с четырьмя резисторами и одним конденсатором. Коэффициенты перед скобками определяют величину проводимости, подключаемую между вычитаемыми напряжениями. Коэффициент при слагаемом, представляющем производную, после введения масштаба времени 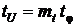 (
(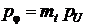 ), определит величину емкости конденсатора, соединенного другим концом с общим проводом.
), определит величину емкости конденсатора, соединенного другим концом с общим проводом.
Построение схемы из электрических аналогов по приведенным уравнениям встречает затруднения, так как некоторые слагаемые имеют отрицательный знак. И хотя, при построении схемы в моделирующем пакете величинам сопротивлений можно присваивать и отрицательные значения, однако схема вычислительной модели оказывается не регулярной и сложной в расчете параметров. Более привлекательной для такого подхода является трех точечная аппроксимация производных. Для достижения той же точности просто необходимо увеличить число узлов в 3 раза. Зато регулярность схемы обеспечена для всех узлов, включая приграничные.

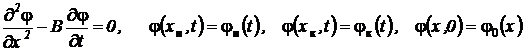 .
.

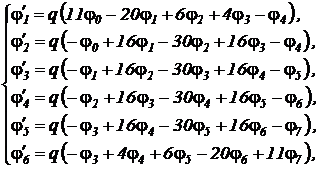 или
или 
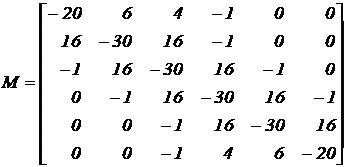 .
.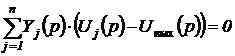 .
.