Общий вид решения, возмущенного погрешностью установки параметра b, представляется следующим образом:
,
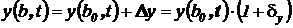где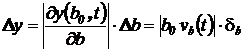 
- абсолютная погрешность решения,
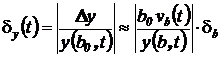- относительная погрешность решения,
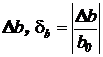- абсолютная и относительная погрешности для b,
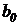- номинальное значение параметра, создающего погрешность.
Под обозначением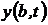 
скрывается любая переменная исходной системы, в том числе и промежуточная, погрешность которой от неточности установки параметра нужно оценить.
В процессе программировании задачи реальные переменные заменяются машинными через посредство масштабных множителей. При решении фиксируются графики или таблицы значений машинных переменных, как функции времени. Полученные моделированием значения переменных, измеренные в вольтах, после подстановки их с соответствующими масштабными множителями в формулы для погрешности, дают расчетные соотношения для оценки допущенной погрешности в следующем виде:
,
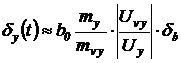где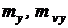 
- масштабные множители для переменной и ее функции чувствительности,
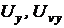- машинные переменные, представляющие переменную y и ее функцию чувствительности.
Аналогично вычисляется погрешность и для любой другой переменной, например, для производной:
.
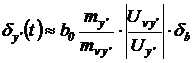