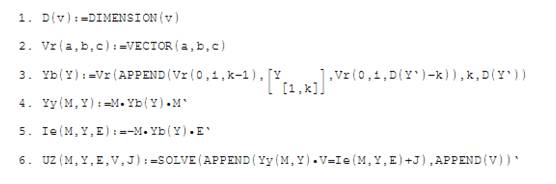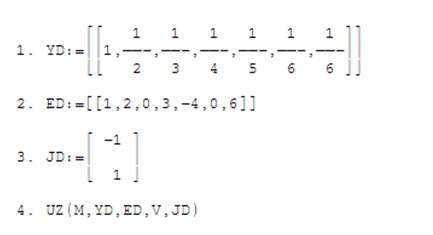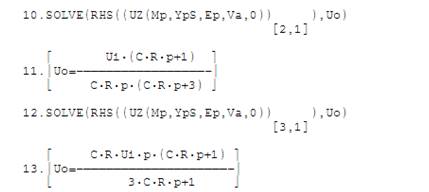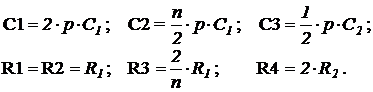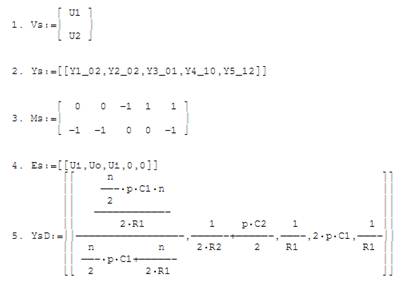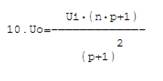Топология заданной RC-цепи описывается матрицей инциденций вершин и ребер. Для того, чтобы безошибочно связать параметры электрической цепи с элементами топологического описания последней, введем однозначные обозначения на схеме и правила заполнения компонентами векторов и матриц для уравнения узловых потенциалов.
Вершинами графа будут узлы схемы, в которых потенциалы относительно общей точки неизвестны. Их необходимо пронумеровать числами натурального ряда от нуля до n. Общая точка обозначается нулем. Вершины друг с другом соединены элементарными ветвями - ребрами.
К ребру (элементарной ветви) отнесем источник ЭДС, если он присутствует, и последовательно присоединенную к нему проводимость. Дадим им обозначения 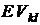 и
и 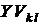 . Здесь k и l (
. Здесь k и l (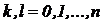 ) являются номерами узлов, между которыми включена ветвь, а
) являются номерами узлов, между которыми включена ветвь, а 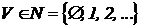 - номер параллельной ветви, включенной между этими же узлами k и l.
- номер параллельной ветви, включенной между этими же узлами k и l.
Порядок записи номеров k и l в индексе должен отражать произвольно выбранное направление тока по ветви. Истинное направление тока, будет определяться знаком числового результата. Знак минус будет свидетельствовать о том, что первоначально выбранное направление тока на самом деле противоположное.
Используя введенные на схеме обозначения, формируем (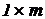 )-матрицу Y из проводимостей
)-матрицу Y из проводимостей 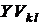 , записанных в произвольном порядке. Для однозначного соответствия исходных обозначений проводимостей введенным обозначениям, запишем и (
, записанных в произвольном порядке. Для однозначного соответствия исходных обозначений проводимостей введенным обозначениям, запишем и (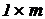 )-матрицу YD данных (в символьном или числовом виде).
)-матрицу YD данных (в символьном или числовом виде).
Для n узлов и m ветвей составляется (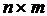 )-матрица инциденций. Строкам сверху вниз соответствуют номера узлов от единицы до n, а столбцам - обозначения проводимостей ребер в том порядке, в котором они записаны в (
)-матрица инциденций. Строкам сверху вниз соответствуют номера узлов от единицы до n, а столбцам - обозначения проводимостей ребер в том порядке, в котором они записаны в (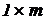 )-матрице проводимостей Y.
)-матрице проводимостей Y.
На пересечении каждой i-той строки (i = 1, 2, ... , n) и каждого 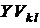 столбца матрицы инциденций записывается элемент множества {0, 1, -1} в соответствии со следующими условиями:
столбца матрицы инциденций записывается элемент множества {0, 1, -1} в соответствии со следующими условиями:
0 , если i не равно индексам k, l;
1 , если i равно индексу k;
-1 , если i равно индексу l.
Воздействие на схему задается (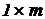 )-матрицей E источников ЭДС в ветвяхи (
)-матрицей E источников ЭДС в ветвяхи (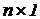 )-матрицей Jузловых задающих токов. Искомой является (
)-матрицей Jузловых задающих токов. Искомой является (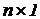 )-матрица узловых потенциалов V с компонентами Vi .
)-матрица узловых потенциалов V с компонентами Vi .
Компонента 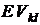 в матрице E соответствуют источнику ЭДС в k,l-той ветви, где последовательно с ней включена проводимость
в матрице E соответствуют источнику ЭДС в k,l-той ветви, где последовательно с ней включена проводимость 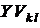 . Записывается компонента со знаком “+”, если направление ЭДС и тока в ветви совпадают, и со знаком минус - в противном случае.
. Записывается компонента со знаком “+”, если направление ЭДС и тока в ветви совпадают, и со знаком минус - в противном случае.
Компонента 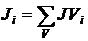 в (
в (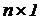 )-матрице J представляет в общем случае алгебраическую сумму токов от задающих источников тока, которые подключены к i-тому узлу. Компонента
)-матрице J представляет в общем случае алгебраическую сумму токов от задающих источников тока, которые подключены к i-тому узлу. Компонента 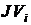 вписывается со знаком "+", если ток источника направлен в узел, и со знаком минус, если ток направлен от узла. Любой источник тока, включенный между узлами k и l, представляется двумя одинаковыми последовательно включенными источниками тока, средняя (общая) точка которых соединена с нулевым узлом.
вписывается со знаком "+", если ток источника направлен в узел, и со знаком минус, если ток направлен от узла. Любой источник тока, включенный между узлами k и l, представляется двумя одинаковыми последовательно включенными источниками тока, средняя (общая) точка которых соединена с нулевым узлом.
Матричное уравнение, из которого находится (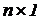 )-матрица узловых потенциалов V, записывается так:
)-матрица узловых потенциалов V, записывается так:
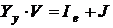 ,
,
где 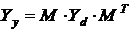 - (
- (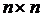 )-матрица узловых проводимостей;
)-матрица узловых проводимостей;
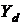 - диагональная (
- диагональная (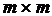 )-матрица, на главной диагонали которой записаны компоненты (
)-матрица, на главной диагонали которой записаны компоненты (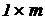 )-матрицы проводимостей Y , а остальные элементы равны нулю;
)-матрицы проводимостей Y , а остальные элементы равны нулю;
J - (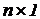 )-матрица узловых задающих токов;
)-матрица узловых задающих токов;
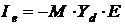 - (
- (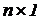 )-матрица эквивалентных узловых токов;
)-матрица эквивалентных узловых токов;
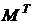 - транспонированная (
- транспонированная (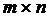 ) матрица инциденций.
) матрица инциденций.
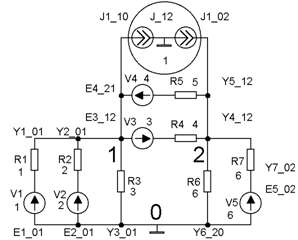
Рисунок 5 |
Пример: На рисунке 5 приведена электрическая схема, включающая в себя межузловые параллельно включенные ветви с источниками и без источников ЭДС и задающий источник тока J_12, ток в котором направлен от узла 1 к узлу 2.
Источник тока заменяем двумя одинаковыми по величине источниками тока с прежним направлением тока: J1_10 и J1_02. Соединив их общий узел с нулевой точкой, получим в результате, что из узла 1 вытекает, а в узел 2 втекает тот же самый ток, что и при одном межузловом источнике.
Для этой схемы названные матрицы с рекомендованными обозначениями их компонент в нотации пакета DERIVE запишутся так:

Процедура (утилита) решения матричного уравнения в операторах пакета DERIVE может быть представлена в следующем виде:
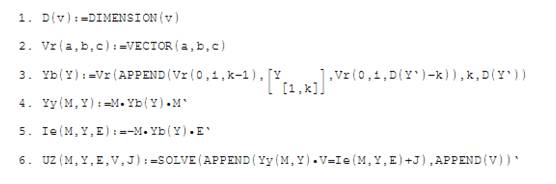
В строке 6 слева записан оператор функции с формальными параметрами, решающий матричное уравнение узловых потенциалов, а справа – определение функции этого оператора.
В качестве фактических параметров для схемы рисунка 5 возьмем конкретные числовые значения проводимостей и ЭДС ветвей и узловых задающих токов в следующем представлении:
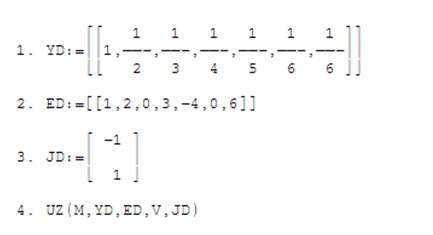
Исполнив процедуру с фактическими параметрами, получим следующую матрицу значений узловых потенциалов:

Единицами измерения в примере были: для сопротивлений - Ом, для напряжений - Вольт и для токов - Ампер.
Получение символьного выражения передаточной функции пассивной схемы с операционным усилителем выполним для схемы, приведенной на рисунке 6.
|
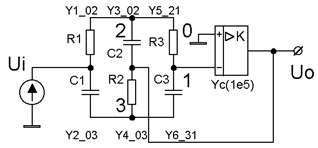
Рисунок 6 |
Все конденсаторы и сопротивления имеют свои схемные обозначения. Проводи-мости всех элементов для удобства составления матричных компонент уравнения узловых потенциалов пронумерованы с учетом выбранного в них направления тока.

Схема имеет 3 внутренних узла, для которых необходимо найти в общем виде операторные выражения в виде функций преобразованных по Лапласу входного и выходного напряжений. Параметрами этих выражений должны быть символьные обозначения компонентов в операторной форме. Пятая строчка приведенных матричных данных как раз и представляет значения схемных проводимостей в операторном виде. Здесь они выражены формулами с одинаковыми значениями R и C .
Матрица задающих токов в данном примере равна нулю.
Подставив матрицы в качестве фактических параметров в оператор решения уравнения узловых потенциалов и выполнив его, получим:

Каждый узловой потенциал в результирующей матрице решения является функцией входного Ui и выходного Uo напряжений. Теперь задача состоит в том, чтобы связать формульной зависимостью выходное напряжение усилителя Uo и напряжение на его входных клеммах. Последнее представляется разностью двух потенциалов: потенциала Up не инвертирующей входной клеммы и потенциала Un инвертирующей входной клеммы. В рассматриваемом примере Up = 0, а Un = U1.
Если обозначить передаточную функцию операционного усилителя через K(p), то в общем случае операторное выражение для напряжения на выходе можно записать так:
Uo = K(p) ( Up - Un ).
Для бесконечно большого и чисто вещественного коэффициента усиления усилителя в диапазоне частот входных сигналов разность входных потенциалов приближенно полагают равной нулю: Up - Un=0.
По отношению к рассматриваемой схеме, для установления зависимости Uo = F(Ui) достаточно приравнять нулю U1 и разрешить полученное уравнение относительно Uo .

Оператор-функция RHS(...) в DERIVE версии 4.02 из логических соотношений вычленяет правую часть. В качестве логического соотношения в рассматриваемом примере выбирается первая строка первого столбца матрицы решения, на что указывают индексы в квадратных скобках у аргумента функции RHS.
Легко получаются и передаточные функции операционного блока, если вход операционного усилителя подключить к узлу 2 или 3. Для этого в операторе решения достаточно изменить индекс строки, например :
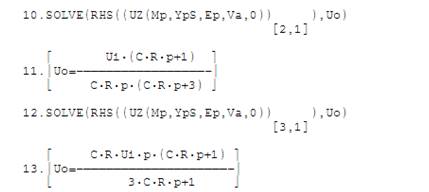
|
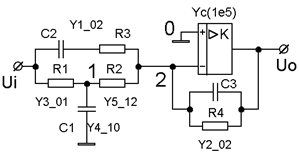
Рисунок 7 |
И, наконец, приведем без особых пояснений еще один пример для схемы рисунка 7, задав для обозначенных на схеме конденсаторов и сопротивлений следующие операторные значения:
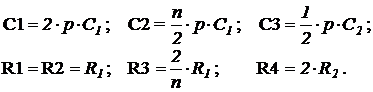
Исходные матрицы для этой схемы будут иметь вид:
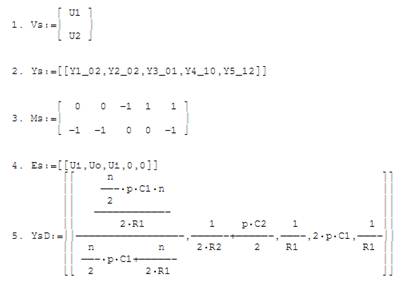
Выражение для потенциала в узле 2 и соотношение выход/вход всего операционного блока:

В полученное в результате решения символьное выражение подставим 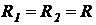 ,
, 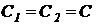 и
и 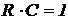 .
.
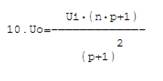
Таким образом, задавая символьные обозначения в операторной форме исходным компонентам и предполагая нулевые начальные условия на реактивных (накопительных) электрических компонентах, в результате последовательных преобразований внешней схемы усилителя или применением метода узловых потенциалов можно получить передаточную функцию операционного блока по одному из выбранных входов в пассивную электрическую цепь.