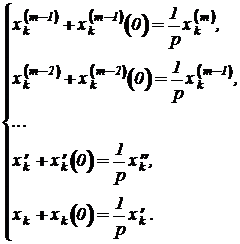Для построения вычислительной модели из операционных блоков необходимо математическую модель объекта моделирования разложить в систему базовых операторов. Базовыми операторами назовем те, для которых в аналоговой или гибридной вычислительной машине имеется обособленный операционный блок. Каждый такой операционный блок передает на свой выход вычисленное значение некоторой исходной или промежуточной переменной. Промежуточным переменным должны быть присвоены имена, отличающиеся от имен в исходной системе уравнений. Присвоение имени каждому базовому оператору и замена базовых операторов в исходной системе введенными именами сводит исходную систему, в конечном счете, к рекурсивной системе алгебраических соотношений. Рекурсивная форма цепи последовательных подстановок или замен переменных характерна для математических моделей объектов с обратными связями.
Обычно физические объекты описываются математическими моделями в форме систем уравнений, представленных суммами однородных функций одинаковой размерности:
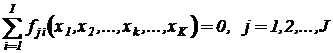 ,
,
где 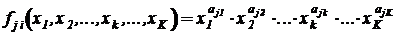 - степенной одночлен со своей размерностью в каждом из уравнений системы, а
- степенной одночлен со своей размерностью в каждом из уравнений системы, а
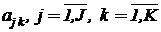 - некоторые действительные числа.
- некоторые действительные числа.
В общем случае 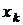 могут быть некоторыми операторами или размерными функциями искомых переменных
могут быть некоторыми операторами или размерными функциями искомых переменных 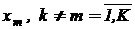 :
:
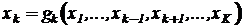 .
.
Базовыми операционными блоками аналоговых вычислительных машин являются блоки, которые выполняют:
- взвешенное алгебраическое суммирование N машинных переменных (электрических напряжений):
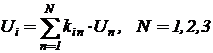 ;
;
- интегрирование и дифференцирование с умножением на коэффициент:
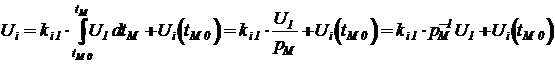 ,
,
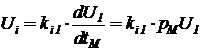 ;
;
- произведение переменных по двум входам с умножением на масштабирующий множитель:
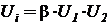 ;
;
- деление переменных с множителем масштабирования:
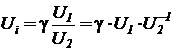 ;
;
- функциональное преобразование одного аргумента, в том числе и элементарными функциями:
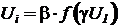 ;
;
- функциональное преобразование двух аргументов:
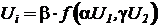 ;
;
- генераторы функций независимого аргумента (времени):
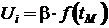 .
.
В приведенных соотношениях для машинной переменной 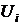 на выходе некоторого i-го операционного блока и машинных переменных
на выходе некоторого i-го операционного блока и машинных переменных 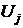 на j-тых входах (
на j-тых входах (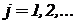 ) этого блока настраиваемыми параметрами являются коэффициенты
) этого блока настраиваемыми параметрами являются коэффициенты 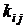 . Параметры a, b, g являются конструктивными. Они вводятся в процессе разработки функциональных блоков и изменению обычно не подлежат.
. Параметры a, b, g являются конструктивными. Они вводятся в процессе разработки функциональных блоков и изменению обычно не подлежат.
Приведенный набор базовых операторов обеспечивает функциональную полноту для достаточно широкого круга прикладных задач с непрерывным изменением переменных. Для моделирования задач с дискретным изменением переменных к составу базовых операционных блоков необходимо добавить, как минимум, фиксатор нулевого порядка с задержкой амплитудного значения на заданное время. Такой блок при непрерывно текущем машинном времени может выполнять функцию оператора сдвига: амплитудное значение входной переменной 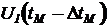 , запомненное в момент времени
, запомненное в момент времени 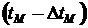 , удерживается в течение одного заданного шага
, удерживается в течение одного заданного шага 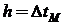 , т.е. смещается по времени вперед на момент
, т.е. смещается по времени вперед на момент 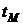 , после чего запоминается и удерживается новое текущее амплитудное значение. Связь выходного напряжения с входным имеет вид:
, после чего запоминается и удерживается новое текущее амплитудное значение. Связь выходного напряжения с входным имеет вид:
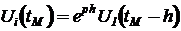
или в обозначениях решетчатых функций целочисленного аргумента k -
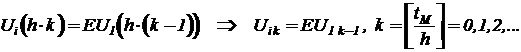 .
.
Зная состав базовых операторов, можно приступать к выделению и обозначению подобных операторов в исходном математическом описании системы.
В однородном мультипликативном одночлене
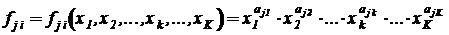
каждый сомножитель может представлять функцию одной или нескольких переменных. В этом случае такой одночлен необходимо представить произведением новых промежуточных переменных, например таких, 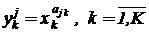 , и системой простых произведений с переменными
, и системой простых произведений с переменными 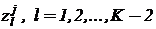 :
:
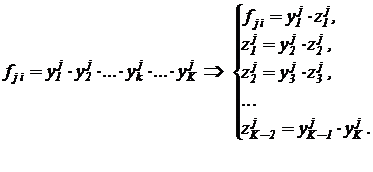
Для вычислительной модели (с точки зрения получения минимальной погрешности и минимального накопления временных задержек) разумнее перемножаемые сомножители разбивать на две по возможности равные группы, для которых затем и вводить имена промежуточных переменных. Многократную разбивку сомножителей на подгруппы удобно сочетать с группировкой сомножителей по порядку их величин. Пары сомножителей произведения обеспечивают минимальную погрешность, если результат произведения близок к максимальному значению используемой шкалы напряжений на операционных блоках.
Аналогичным образом выполняют разложение на базовые операторы с ограниченным числом входных переменных участков исходной системы уравнений, представленных алгебраическими суммами:
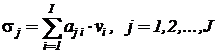 .
.
В зависимости от общего числа слагаемых I можно использовать базовые сумматоры на N=2 или N=3 входа. Для этого исходную сумму разбивают на 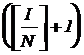 групп, которым дают имена промежуточных переменных. Если число введенных промежуточных переменных окажется больше N , их опять разбивают на группы, пока не останется одна выходная переменная
групп, которым дают имена промежуточных переменных. Если число введенных промежуточных переменных окажется больше N , их опять разбивают на группы, пока не останется одна выходная переменная 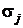 .
.
Если среди операторов, входящих в каждое уравнение системы, входят производные искомых переменных, то каждое из уравнений системы разрешается относительно старшей производной переменной состояния. Правая часть полученных равенств раскладывается на базовые операторы по тем правилам, которые описаны выше. Вид одного из определяющих уравнений, в левой части которого стоит старшая производная переменной состояния, будет следующим:
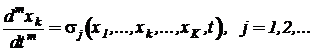 .
.
Производная переменной состояния заменяется m-кратным интегрированием по времени левой и правой частей с введением при каждом очередном интегрировании имени новой промежуточной переменной, если в исходной системе производной более низкого порядка не было:
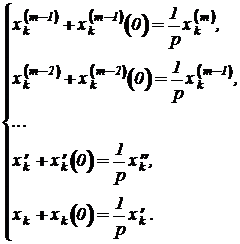
Здесь 1/p - символическое обозначение оператора интегрирования по времени, а степень в скобках - порядок производной. Производные в точке ноль - есть значения начальных условий, которые обязаны быть заданными для исходной системы.

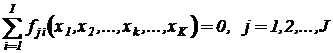 ,
,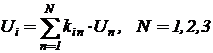 ;
; 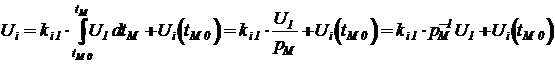 ,
,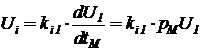 ;
;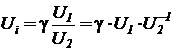 ;
;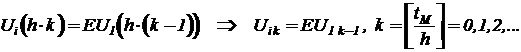 .
.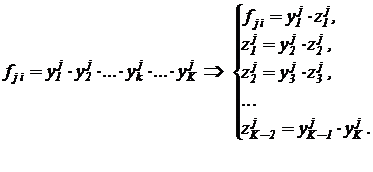
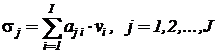 .
.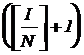 групп, которым дают имена промежуточных переменных. Если число введенных промежуточных переменных окажется больше N , их опять разбивают на группы, пока не останется одна выходная переменная
групп, которым дают имена промежуточных переменных. Если число введенных промежуточных переменных окажется больше N , их опять разбивают на группы, пока не останется одна выходная переменная 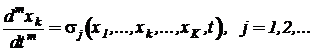 .
.