Программирование задачи моделирования заключается во взаимно однозначном отображении структуры и параметров математической модели исследуемого объекта на структуру и параметры вычислительной модели.
Математическая модель объекта исследования представляется системой дифференциальных или разностных уравнений, независимая переменная которых определяет непрерывное или дискретное изменение состояний объекта.
Вычислительная модель объекта исследования на аналоговых или цифровых операционных блоках в качестве независимой переменной в первом случае использует реальное время и во втором случае - квантованное реальное время, определяемое встроенным тактирующим генератором. То, что независимая переменная в вычислительных моделях является временем, предопределяет и правила, по которым устанавливается ее взаимосвязь с независимой физической переменной, относительно которой развертываются процессы в математической модели объекта.
Для исследования динамики математической модели ее независимую переменную x удобнее всего уподобить физическому времени t, которое всегда изменяется непрерывно и равномерно в положительном направлении. В этом случае упрощается задача линейной однозначной связи реальной независимой переменной с машинным временем вычислительной модели tM, которая также изменяется только в положительном направлении.
При равномерном изменении независимых переменных их взаимосвязь будем представлять следующим образом:
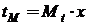 ,
,
где Mt - масштабный множитель с размерностью 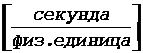 .
.
x - реальная независимая переменная, возможно уже приведенная в математической модели к безразмерной величине интервала [0,1).
В случае квантованного времени и алгоритмической реализации дифференциально-интегральных операторов и нелинейных функций взаимосвязь независимых переменных должна устанавливаться между их дифференциалами или приращениями:
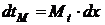
или
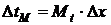 .
.
Масштабный множитель (коэффициент) в линейной зависимости находится путем сопоставления дифференциалов, минимальных квантов или характерных приращений независимых переменных математической и вычислительной модели, однозначно увязываемых с периодами колебательных процессов, частотами и т.д.:
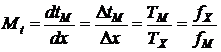 .
.
Математические модели динамических объектов в качестве независимой переменной имеют абсолютное 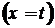 или относительное время
или относительное время 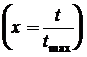 , измеряемое соответственно в секундах или единицах относительного диапазона.
, измеряемое соответственно в секундах или единицах относительного диапазона.
В аналоговых вычислительных машинах развертка процессов исторически привязывалась к секундному диапазону, в котором главной гармонической составляющей с максимальной амплитудой являлась частота 1 Гц. Такие скорости изменения считались вполне доступными для отслеживания человеком непрерывно развертываемых процессов и предъявляли не слишком высокие требования к максимальным рабочим частотам операционных блоков и усилителей (10 - 100 Гц). Для машин с периодизацией решения рабочие частоты увеличивали до 103 - 104 Гц, что при прочих равных условиях требовало соответствующего расширения в высокочастотную область полосы усиливаемых частот операционными усилителями. Для таких машин развертку реальных процессов в объекте удобно было привязывать к миллисекундному диапазону вычислительной модели, для которого главной гармонической составляющей с максимальной амплитудой являлась частота 1000 Гц.
Если в качестве аналоговой или гибридной вычислительной машины использовать ее вычислительную модель, созданную в среде программного пакета моделирования электронных схем, например, Micro-Cap V, то иногда в качестве главной гармонической составляющей развертываемых процессов удобно брать 1000 Гц. Это ни в коей мере не повлияет на скорость получения решений, однако, будет более удобно вписываться в характеристики пользовательского интерфейса, так как масштабирование времени в пакете ориентировано в большей части на частотный диапазон радиоэлектронных схем.
Порядок величин масштабных множителей для независимой переменной всецело зависит от характера протекания процессов в описанном реальном объекте. Медленные биологические или химические процессы с циклическими изменениями длительностью в год (~107 c), месяц (~106 c), день (~105 c), час (~103 c), минуту (~102 c) путем привязки к машинному интервалу в одну секунду воспроизводятся в своих вычислительных моделях в ускоренном темпе. При этом 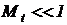 . Быстрые электрические и электромагнитные процессы, с реальными основными периодическими составляющими в миллисекунды (~10-3 c) или микросекунды (~10-6 c) в результате привязки к односекундному интервалу вычислительной модели замедляются многократно: в
. Быстрые электрические и электромагнитные процессы, с реальными основными периодическими составляющими в миллисекунды (~10-3 c) или микросекунды (~10-6 c) в результате привязки к односекундному интервалу вычислительной модели замедляются многократно: в 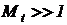 раз.
раз.
Случай 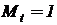 при использовании чисто аналоговых операционных блоков соответствует развертыванию процессов в вычислительной модели в темпе протекания процессов в реальном объекте, т.е. в реальном времени. Вычислительные модели отдельных блоков, работающие в реальном времени, через согласующие элементы могут включаться в реально функционирующие системы и, наоборот: к вычислительной модели системы могут подключаться реальные блоки.
при использовании чисто аналоговых операционных блоков соответствует развертыванию процессов в вычислительной модели в темпе протекания процессов в реальном объекте, т.е. в реальном времени. Вычислительные модели отдельных блоков, работающие в реальном времени, через согласующие элементы могут включаться в реально функционирующие системы и, наоборот: к вычислительной модели системы могут подключаться реальные блоки.
Если используются цифровые вычислительные модели аналоговых операционных блоков, то случай 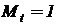 еще не определяет возможность работы вычислительной модели объекта в реальном времени и возможность ее включения в работу с реальной аппаратурой. Чтобы вычислительная модель объекта с цифровыми операционными блоками функционировала в реальном времени необходима синхронная выдача результатов операций с каждого операционного блока. При этом минимальный квант времени, определяющий частоту синхронизации и равные ему приращения времени в вычислительной модели и объекте, должен быть больше или равен наибольшему из всех времен, затрачиваемых операционными блоками на получение результата операции.
еще не определяет возможность работы вычислительной модели объекта в реальном времени и возможность ее включения в работу с реальной аппаратурой. Чтобы вычислительная модель объекта с цифровыми операционными блоками функционировала в реальном времени необходима синхронная выдача результатов операций с каждого операционного блока. При этом минимальный квант времени, определяющий частоту синхронизации и равные ему приращения времени в вычислительной модели и объекте, должен быть больше или равен наибольшему из всех времен, затрачиваемых операционными блоками на получение результата операции.
В пакетах моделирования электронных схем параллельно работающих операционных блоков принципиально нет. Все вычислительные модели операционных блоков обрабатываются последовательно одним процессорным устройством. Поэтому время, затрачиваемое на моделирование, зависит от числа операционных блоков в структуре вычислительной модели объекта, во-первых, от сложности вычислительной модели примененных операционных блоков, во-вторых, и интерфейсных услуг моделирующего пакета, в-третьих. Масштабирование независимых переменных проявляется лишь в оцифровке временной оси на графиках развертываемых процессов вычислительной модели.
Для удобства пересчета времени вычислительной модели во время (или другой физической природы независимую переменную) математической модели объекта масштабный множитель обычно выбирают кратным десяти.

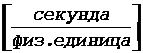 .
.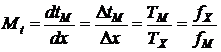 .
.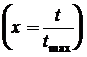 , измеряемое соответственно в секундах или единицах относительного диапазона.
, измеряемое соответственно в секундах или единицах относительного диапазона.