Расчет линейных электрических цепей в большинстве своем основан на последовательном применении ряда эквивалентных преобразований отдельных фрагментов схемы, с целью сведения их к каноническим формам, для которых установлены конечные формульные соотношения между токами и напряжениями в заданных точках. Параметрами в этих соотношениях выступают числовые значения схемных электрических компонентов.
Основные соотношения, связывающие электрический ток и падение напряжения на линейных электрических компонентах, вытекают из закона Ома - для сопротивлений, из закона Гаусса - для конденсаторов и из закона Фарадея - для индуктивностей:
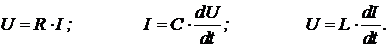
Переменными, описывающими состояние электрической цепи, являются токи и напряжения. В общем случае они изменяются во времени, поэтому при анализе цепей должны рассматриваться, как функции действительной переменной. Если использовать в законах Кирхгофа эти соотношения, то процессы в электрической цепи будут описаны системой линейных дифференциальных уравнений. Интегрирование системы дифференциальных уравнений, особенно высокого порядка, может оказаться достаточно сложной задачей.
Облегчить задачу получения решений для линейного случая можно, если перейти из области вещественной переменной в область комплексной переменной, применив интегральное преобразование Лапласа (п. 5.1.1):
.
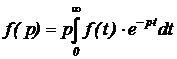Основное достоинство этого преобразования состоит в том, что операторы интегрирования, дифференцирования и их линейные комбинации преобразуются в алгебраические выражения, в которых функции действительной переменной представляются функциями комплексного аргумента. Для изображения обычно сохраняют то же символьное обозначение функции. Признаком функции комплексной переменной служит символ для аргумента p или s (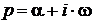
).
Применив преобразование Лапласа к соотношениям для токов и напряжений, получим их комплексные изображения следующего вида:
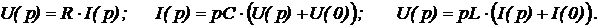
При преобразовании соотношений пассивных цепей начальные значения напряжений на конденсаторах и токов в индуктивностях можно полагать равными нулю и учитывать лишь в конечных выражениях.
В комплексном виде все выражения по форме подобны закону Ома. Это дает право рассматривать параметры этих соотношений, как комплексные выражения сопротивлений или проводимостей:
комплексные сопротивления -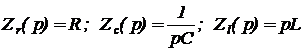 
;
комплексные проводимости -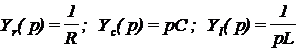 
.
Для компактности записи выражений в преобразованном по Лапласу виде, скобки с комплексным параметром будем опускать. Там, где может возникнуть двусмысленность в толковании выражения, скобки с соответствующим аргументом будут проставлены.
Например, на рисунке 1 показана линейная электрическая схема для алгебраического суммирования n входных напряжений от n источников, каждый из которых включен между общим проводом и соответствующей входной клеммой. Так как элементы схемы по величине постоянны, то в свете сказанного о преобразовании Лапласа, можно полагать, что в приведенной схеме на вход поданы напряжения, как функции комплексной переменной, и проводимости (или сопротивления) представлены комплексными выражениями. Поэтому выражение для выходного напряжения может быть записано в виде функции комплексной переменной следующим образом:
|
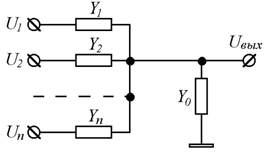
Рисунок 1. |
В случае использования в этой звездообразной схеме емкостей и индуктивностей, в приведенное соотношение необходимо подставлять соответствующие комплексные выражения проводимостей.
Схема рисунка 1 может быть заменена эквивалентной схемой, состоящей из одного источника ЭДС с последовательно включенным сопротивлением (проводимостью), как показано на рисунке 2.
|
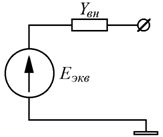
Рисунок 2 |
Выражения для внутренней проводимости и внутреннего сопротивления, являющегося обратной величиной, будут такими:
.
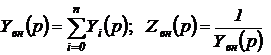Выражение для эквивалентной ЭДС, которую, в принципе, можно измерить на выходных клеммах измерительным прибором, не потребляющим тока, получит следующий вид:
.
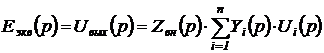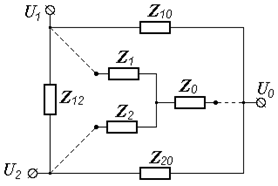
Рисунок 3 |
Распространенным локальным эквивалентным преобразованием линейных схем является замена трехполюсного звездообразного фрагмента трехполюсным треугольным.
На рисунке 3 выделен из некоторой схемы трехполюсный фрагмент, на котором для наглядности совмещены два вида эквивалентных трехполюсников.
В трех узлах, потенциалы которых обозначены как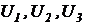 
, последние не изменятся, если вместо треугольного соединения сопротив-лений 
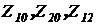включить звезду из сопротивлений 
.
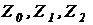Пересчет сопротивлений звезды и проводимостей треугольника выполняется по следующим формулам:
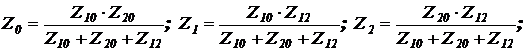
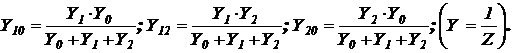
Формулы для замены параллельного соединения сопротивлений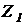 
и 
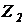одним:
.
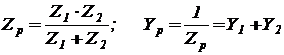Формулы для замены последовательного соединения сопротивлени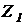й 
и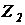 
одним:
.
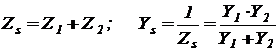Двухполюсная ветвь, состоящая из последовательного соединения сопротивления и источника ЭДС (как на рисунке 2), может быть заменена параллельным соединением этого сопротивления и источника тока. Ток источника направлен к положительному полюсу источника ЭДС, а величина его рассчитывается по формуле: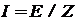 
. Один источник тока в ряде случаев удобно представлять двумя, из которых один задает входящий ток, а второй, такой же по величине, - выходящий.
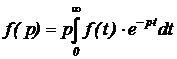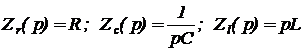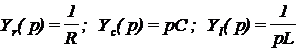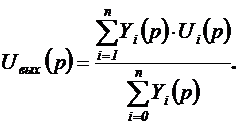
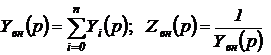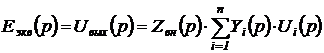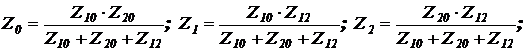
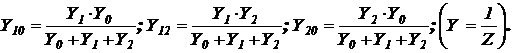
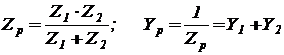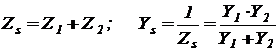