Означення 7.4.Диференціальне рівняння першого порядку називається лінійним, якщо і сама невідома функція і її похідна входять в це рівняння лише у першому степені й не містять їх добутку.
Загальний вигляд лінійного рівняння першого порядку
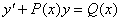 (7.16)
(7.16)
Якщо у рівнянні (7.16) права частина функція 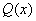 не дорівнює тотожньо нулю, то таке рівняння називають лінійним неоднорідним диференціальним рівнянням першого порядку.
не дорівнює тотожньо нулю, то таке рівняння називають лінійним неоднорідним диференціальним рівнянням першого порядку. 
Якщо ж 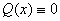 , то рівняння
, то рівняння
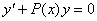 (7.17)
(7.17)
називають лінійним однорідним диференціальним рівняннм першого порядку.
Розглянемо один із можливих методів розв’язання лінійного диференціального рівняння першого порядку.
Шукаємо розв’язок лінійного рівняння у вигляді добутку двох функцій х
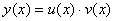 (7.18)
(7.18)
Тим самим шуканими стають функції 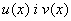 , одну з яких можна вибрати довільно, а друга – має визначатися рівнянням.
, одну з яких можна вибрати довільно, а друга – має визначатися рівнянням.
Диференціюємо обидві частини цієї рівності
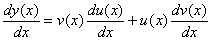
Підставимо вирази для 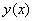 і
і 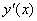 у рівняння (7.16). Маємо
у рівняння (7.16). Маємо
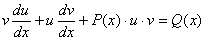 ,
,
або
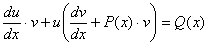 .
.
Підберемо функції u i v так, щоб виконувалися рівності
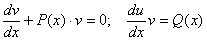 .
.
Звідси
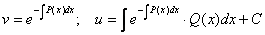
Остаточно дістанемо загальний розв’язок рівняння (7.16) у вигляді
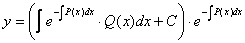 .
.
Приклад.
Зінтегрувати диференціальне рівняння
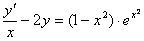
Розв’язання. Це лінійне неоднорідне рівняння першого порядку. Зведемо його до вигляду (7.16) (хоча це необов’язково). Для чого обидві частини рівняння помножимо на х. Дістанемо
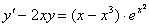 .
.
Покладемо
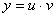 .
.
Диференціюємо цю рівність по х:
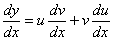 .
.
Замінимо в рівнянні 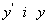 їх виразами через u i v, маємо
їх виразами через u i v, маємо
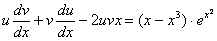
Згрупуємо члени, що містять функцію u, і винесемо цю функцію за дужки. Дістанемо:
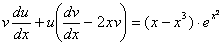
Знайдемо тепер таку функцію v, щоб
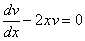 (1)
(1)
За цієї умови, маємо
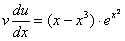 (2)
(2)
Розв’яжемо рівняння (1), відокремивши змінні:
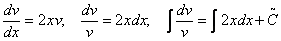
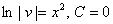 .
.
За означенням логарифма
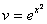
Підставляючи знайдене значення v в рівняння (2), дістанемо
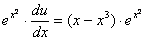
або
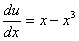
Це рівняння з відокремлюваними змінними. Розв’язавши його, знайдемо
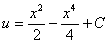
Остаточно загальний розв’язок рівняння дістанемо у вигляді
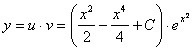 .
.
До лінійного рівняння заміною 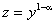 зводять так зване рівняння Бернуллі
зводять так зване рівняння Бернуллі
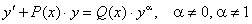 (6.19)
(6.19)


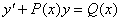 (7.16)
(7.16)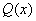 не дорівнює тотожньо нулю, то таке рівняння називають лінійним неоднорідним диференціальним рівнянням першого порядку.
не дорівнює тотожньо нулю, то таке рівняння називають лінійним неоднорідним диференціальним рівнянням першого порядку. 
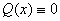 , то рівняння
, то рівняння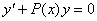 (7.17)
(7.17)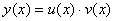 (7.18)
(7.18)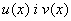 , одну з яких можна вибрати довільно, а друга – має визначатися рівнянням.
, одну з яких можна вибрати довільно, а друга – має визначатися рівнянням.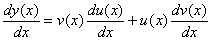
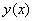 і
і 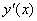 у рівняння (7.16). Маємо
у рівняння (7.16). Маємо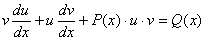 ,
,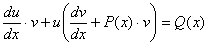 .
.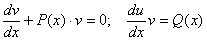 .
.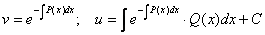
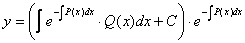 .
.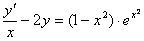
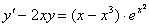 .
.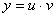 .
.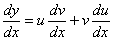 .
.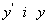 їх виразами через u i v, маємо
їх виразами через u i v, маємо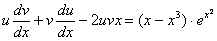
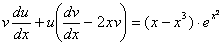
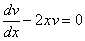 (1)
(1)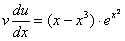 (2)
(2)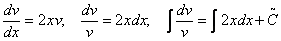
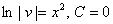 .
.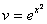
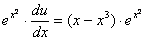
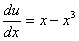
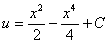
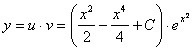 .
.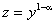 зводять так зване рівняння Бернуллі
зводять так зване рівняння Бернуллі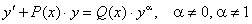 (6.19)
(6.19)