Функцію 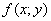 називають однорідною функцією виміру m відносно своїх аргументів х і у, якщо вона справджує тотожність
називають однорідною функцією виміру m відносно своїх аргументів х і у, якщо вона справджує тотожність
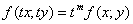 , (7.12)
, (7.12)
де t - ,будь-який множник.
Так, наприклад, функції 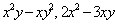 ,
, 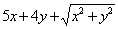 однорідні: перша – третього виміру, друга – другого виміру і третя – першого виміру.
однорідні: перша – третього виміру, друга – другого виміру і третя – першого виміру.
Означення 7.3.Диференціальне рівняння 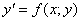 називається однорідним, якщо його права частина функція
називається однорідним, якщо його права частина функція 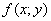 є однорідною функцією нульового виміру відносно своїх аргументів х і у.
є однорідною функцією нульового виміру відносно своїх аргументів х і у.
Інтегрування однорідного рівняння (7.12) за допомогою спеціальної підстановки зводиться до інтегрування рівняння з відокремлюваними змінними.
Насправді, враховуючи нульовий вимір однорідності функції 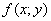 , для будь-якого t маємо
, для будь-якого t маємо
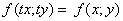 . Зокрема, покладемо
. Зокрема, покладемо 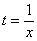 , дістанемо:
, дістанемо:
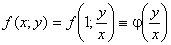
Рівняння (7.12) запишеться у вигляді
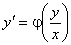 .
.
Введемо нову невідому функцію и задопомогою підстановки: 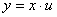 ,
, 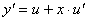 .
.
Дістанемо рівняння
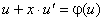 ,
,
в якому змінні відокремлюються:
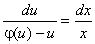 (7.13)
(7.13)
Звідси знаходимо загальний інтеграл рівняння у вигляді:
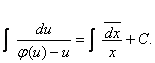 де С - довільна стала.
де С - довільна стала.
Насамкінець, після обчислення інтегралів і заміни допоміжної функції и її виразом через х і у, знайдемо розв’язок однорідного рівняння.
Приклад.
Зінтегрувати рівняння
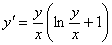 .
.
Розв’язання. Це однорідне диференціальне рівняння першого порядку. Застосуємо підстановку
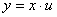 ,
, 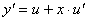 ,
,
тоді
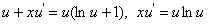
- рівняння з відокремлюваними змінними відносно и. Розв’зуючи його, дістанемо
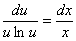 -
-
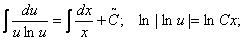
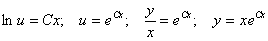 -
-
загальний розв’язок рівняння.
Зауваження. Рівняння виду
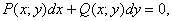 (7.14)
(7.14)
в якому функції 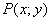 та
та 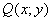 - однорідні відносно своїх аргументів х і у функції одного і того ж виміру є однорідним і заміною
- однорідні відносно своїх аргументів х і у функції одного і того ж виміру є однорідним і заміною 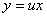 зводиться до рівняння з відокремлюваними змінними.
зводиться до рівняння з відокремлюваними змінними.
Приклад.
Зінтегрувати рівняння
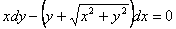 .
.
Розв’язання. Це рівняння однорідне. Заміна
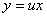 ,
, 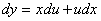
приводить його до рівняння
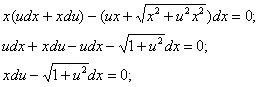
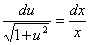 - з відокремленими змінними.
- з відокремленими змінними.
Інтегруючи, знаходимо
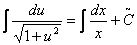 ;
; 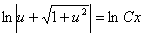 ;
; 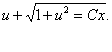
Підставивши 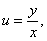 дістаємо,після перетворень, загальний інтеграл вихідного рівняння
дістаємо,після перетворень, загальний інтеграл вихідного рівняння 

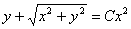 .
.
Вкажемо, нарешті, один клас рівнянь, які зводяться до однорідного:
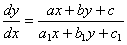 (7.15)
(7.15)
Для цього досить зробити заміну
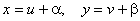 ,
,
де вибрати параметри 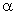 і
і 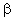 так, щоб
так, щоб
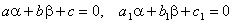 .
.
Вправи
Зінтегрувати диференціальні рівняння:
1. 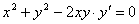 (Відповідь:
(Відповідь: 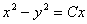 )
)
2. 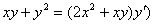 (Відповідь:
(Відповідь: 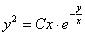 )
)
3. 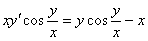 (Відповідь:
(Відповідь: 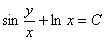 )
)
4. 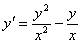 (Відповідь:
(Відповідь: 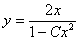 )
)


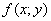 називають однорідною функцією виміру m відносно своїх аргументів х і у, якщо вона справджує тотожність
називають однорідною функцією виміру m відносно своїх аргументів х і у, якщо вона справджує тотожність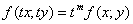 , (7.12)
, (7.12)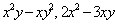 ,
, 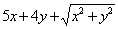 однорідні: перша – третього виміру, друга – другого виміру і третя – першого виміру.
однорідні: перша – третього виміру, друга – другого виміру і третя – першого виміру.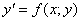 називається однорідним, якщо його права частина функція
називається однорідним, якщо його права частина функція 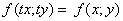 . Зокрема, покладемо
. Зокрема, покладемо 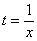 , дістанемо:
, дістанемо: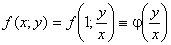
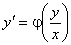 .
.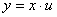 ,
, 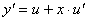 .
.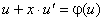 ,
,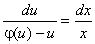 (7.13)
(7.13)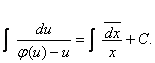 де С - довільна стала.
де С - довільна стала.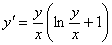 .
.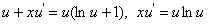
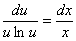 -
-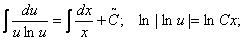
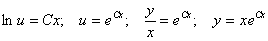 -
-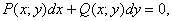 (7.14)
(7.14) 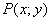 та
та 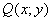 - однорідні відносно своїх аргументів х і у функції одного і того ж виміру є однорідним і заміною
- однорідні відносно своїх аргументів х і у функції одного і того ж виміру є однорідним і заміною 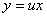 зводиться до рівняння з відокремлюваними змінними.
зводиться до рівняння з відокремлюваними змінними.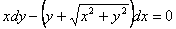 .
.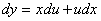
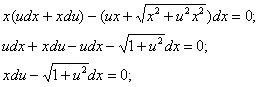
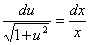 - з відокремленими змінними.
- з відокремленими змінними.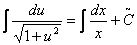 ;
; 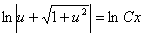 ;
; 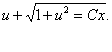
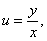 дістаємо,після перетворень, загальний інтеграл вихідного рівняння
дістаємо,після перетворень, загальний інтеграл вихідного рівняння 
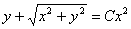 .
.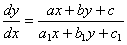 (7.15)
(7.15)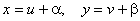 ,
,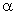 і
і 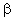 так, щоб
так, щоб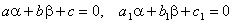 .
.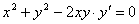 (Відповідь:
(Відповідь: 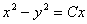 )
)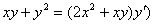 (Відповідь:
(Відповідь: 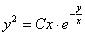 )
)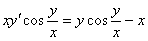 (Відповідь:
(Відповідь: 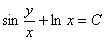 )
)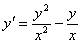 (Відповідь:
(Відповідь: 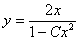 )
)