Розв’яжемо лінійне неоднорідне рівняння другого порядку з сталими коефіцієнтами рівняння
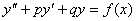 . (7.39)
. (7.39)
Загальним розв’язком рівняння (7.39) є функція
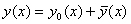 , (7.40)
, (7.40)
де 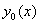 - загальний розв’язок відповідного однорідного рівняння
- загальний розв’язок відповідного однорідного рівняння
 , (7.41)
, (7.41)
характеристичне рівняння якого
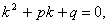 (7.42)
(7.42)
а 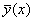 - довільний частинний розв’язок неоднорідного рівняння.
- довільний частинний розв’язок неоднорідного рівняння.
У повних курсах вивчається так званий метод варіації сталих, який дає можливість при будь-якому вигляді неперервної функції  дістати частинний розв’язок неоднорідного рівняння.
дістати частинний розв’язок неоднорідного рівняння.
Ми вкажемо метод знаходження частинного розв’язку неоднорідного рівняння з сталими коефіцієнтами (7.37), у випадку правих частин певного частинного вигляду.
Якщо права частина  рівняння (7.39) має вигляд
рівняння (7.39) має вигляд
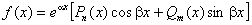 . (7.43)
. (7.43)
де 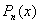 і
і 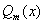 - многочлени з дійсними коефіцієнтами,
- многочлени з дійсними коефіцієнтами, 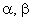 - дійсні числа (можуть дорівнювати і нулю), то рівняння(7.39) має такий частинний розв’язок
- дійсні числа (можуть дорівнювати і нулю), то рівняння(7.39) має такий частинний розв’язок
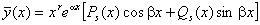 (7.44)
(7.44)
Тут r – кратність кореня 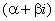 для характеристичного рівняння (7.42) (якщо
для характеристичного рівняння (7.42) (якщо 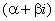 не є коренем характеристичного рівняння, то слід покласти r=0); число
не є коренем характеристичного рівняння, то слід покласти r=0); число 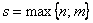 ;
; 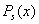 і
і 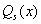 - многочлени степеня s з невизначеними коефіцієнтами.
- многочлени степеня s з невизначеними коефіцієнтами.
Наведемо таблицю простіших правих частин (7.43) і укажемо вигляд частинного розв’язку за формулою (7.44).
| Вигляд правої частини рівняння (6.39)
| Вигляд частинного розв’язку
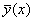
|
(А – число)
| 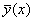 =В, якщо О не є коренем
характеристичного рівняння (7.42); =В, якщо О не є коренем
характеристичного рівняння (7.42);
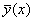 =Вх, якщо О є однократним коренем; =Вх, якщо О є однократним коренем;
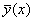 =Вх2, якщо О є двократним коренем
(В – число, яке треба обчислити). =Вх2, якщо О є двократним коренем
(В – число, яке треба обчислити).
|
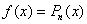 [
[ 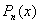 - многочлен n–го степеня] - многочлен n–го степеня]
| 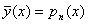 , якщо О не є коренем характе-
ристичного рівняння (7.42); , якщо О не є коренем характе-
ристичного рівняння (7.42);
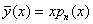 , якщо О є однократним коренем; , якщо О є однократним коренем;
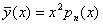 ,якщо О є двократним коренем
[ ,якщо О є двократним коренем
[ 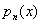 - многочлен n-гостепеня, коефіцієнти якого
треба обчислити] - многочлен n-гостепеня, коефіцієнти якого
треба обчислити]
|
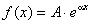 (A i a - дійсні числа) (A i a - дійсні числа)
| 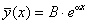 ,якщо a не є коренем характе-
ристичного рівняння(7.42); ,якщо a не є коренем характе-
ристичного рівняння(7.42);
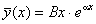 ,якщо a є однократним коренем; ,якщо a є однократним коренем;
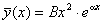 , якщо a є двократним коренем
(В – число, яке треба обчислити) , якщо a є двократним коренем
(В – число, яке треба обчислити)
|
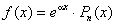 [a - дійсне число,
[a - дійсне число, 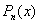 - многочлен n-го степеня] - многочлен n-го степеня]
| 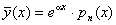 ,якщо a не є коренем характеристичного рівняння (7.42); ,якщо a не є коренем характеристичного рівняння (7.42);
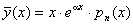 , якщо a є однократним коренем; , якщо a є однократним коренем;
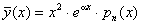 ,якщо a є двократним коренем[ ,якщо a є двократним коренем[ 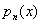 - многочлен n-го степеня,
коефіцієнти якого треба обчислити ] - многочлен n-го степеня,
коефіцієнти якого треба обчислити ]
|
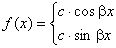 (с і
(с і 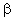 - дійсні числа) - дійсні числа)
| 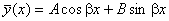 ,
якщо ,
якщо 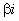 не є коренем
характеристичного рівняння
(7.42); не є коренем
характеристичного рівняння
(7.42);
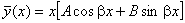 ,
якщо ,
якщо 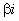 є однократним
коренем
(А і В – числа, які треба обчислити) є однократним
коренем
(А і В – числа, які треба обчислити)
|
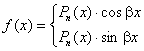 [
[ 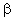 - дійсне число, - дійсне число, 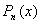 -многочлен n-го степеня] -многочлен n-го степеня]
| 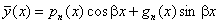 ,
якщо ,
якщо 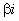 не є коренем характе-
ристичного рівняння(6.42); не є коренем характе-
ристичного рівняння(6.42);
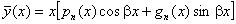 ,
якщо ,
якщо 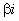 є однократним коренем
[ є однократним коренем
[ 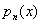 і і 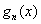 – многочлени
n-го порядку, коефіцієнти
яких треба обчислити ] – многочлени
n-го порядку, коефіцієнти
яких треба обчислити ]
|
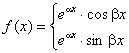 (a і
(a і 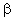 - дійсні числа) - дійсні числа)
| 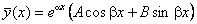 ,
якщо ,
якщо 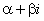 не є коренем
характеристичного рівняння
(6.42); не є коренем
характеристичного рівняння
(6.42);
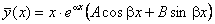 ,
якщо ,
якщо 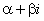 є однократним
коренем
(А і В – числа, які треба
обчислити) є однократним
коренем
(А і В – числа, які треба
обчислити)
|
Приклади.
1. Знайти загальний розв’язок рівняння
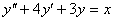 .
.
Розв’язання. Загальний розв’язок шукаємо у вигляді
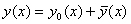 .
.
В першу чергу знаходимо 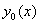 - загальний розв’язок відповідного однорідного рівняння
- загальний розв’язок відповідного однорідного рівняння
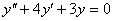 .
.
Характеристичне рівняння  має корені
має корені 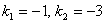 . Тому загальний розв’язок однорідного рівняння записуємо у вигляді
. Тому загальний розв’язок однорідного рівняння записуємо у вигляді
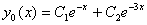 .
.
Частинний розв’язок неоднорідного рівняння шукаємо у вигляді
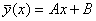 .
.
Щоб обчислити числа А і В, знайдемо 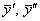 і підставимо їх у вхідне рівняння:
і підставимо їх у вхідне рівняння:
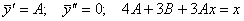 .
.
Прирівнюємо коефіцієнти при однакових степенях х, маємо
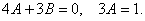
Звідси 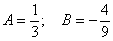 .
.
Частинний розв’язок такий:
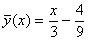 .
.
Загальний розв’язок рівняння
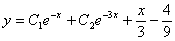
2. Знайти загальний розв’язок рівняння
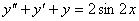 .
.
Розв’язання. Загальний розв’язок однорідного рівняння:
 ;
;
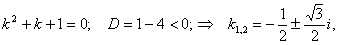
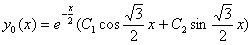 .
.
Частинний розв’язок неоднорідного рівняння:
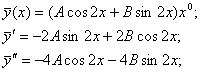
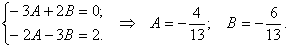
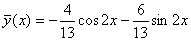
Загальний розв’язок неоднорідного рівняння
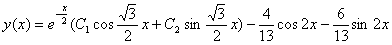 .
.
Вправи
Знайти загальні розв’язки рівнянь
1. 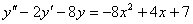 (Відп.
(Відп. 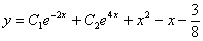 )
)
2. 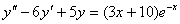 (Відп.
(Відп. 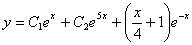 )
)
3. 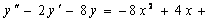 (Відп.
(Відп. 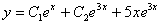 )
)
4. 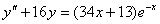 (Відп.
(Відп. 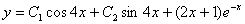 )
)
5. 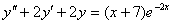 (Відп.
(Відп.  )
)
6.  (Відп.
(Відп. 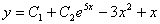 )
)
7. 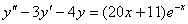 (Відп.
(Відп. 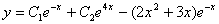 )
)
8. 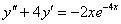 (Відп.
(Відп. 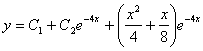 )
)
9. 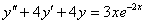 (Відп.
(Відп. 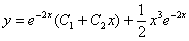 )
)
10. 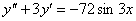 (Відп.
(Відп.  )
)
11. 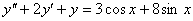 (Відп.
(Відп. 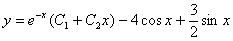 )
)
12. 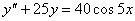 (Відп.
(Відп. 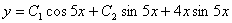 )
)
13. 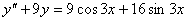 (Відп.
(Відп.


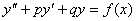 . (7.39)
. (7.39)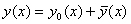 , (7.40)
, (7.40)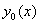 - загальний розв’язок відповідного однорідного рівняння
- загальний розв’язок відповідного однорідного рівняння , (7.41)
, (7.41)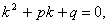 (7.42)
(7.42)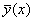 - довільний частинний розв’язок неоднорідного рівняння.
- довільний частинний розв’язок неоднорідного рівняння. дістати частинний розв’язок неоднорідного рівняння.
дістати частинний розв’язок неоднорідного рівняння.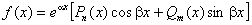 . (7.43)
. (7.43)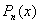 і
і 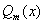 - многочлени з дійсними коефіцієнтами,
- многочлени з дійсними коефіцієнтами, 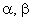 - дійсні числа (можуть дорівнювати і нулю), то рівняння(7.39) має такий частинний розв’язок
- дійсні числа (можуть дорівнювати і нулю), то рівняння(7.39) має такий частинний розв’язок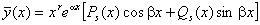 (7.44)
(7.44)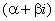 для характеристичного рівняння (7.42) (якщо
для характеристичного рівняння (7.42) (якщо 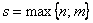 ;
; 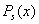 і
і 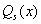 - многочлени степеня s з невизначеними коефіцієнтами.
- многочлени степеня s з невизначеними коефіцієнтами.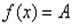
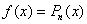 [
[ 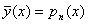 , якщо О не є коренем характе-
ристичного рівняння (7.42);
, якщо О не є коренем характе-
ристичного рівняння (7.42);
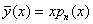 , якщо О є однократним коренем;
, якщо О є однократним коренем;
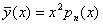 ,якщо О є двократним коренем
[
,якщо О є двократним коренем
[ 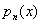 - многочлен n-гостепеня, коефіцієнти якого
треба обчислити]
- многочлен n-гостепеня, коефіцієнти якого
треба обчислити]
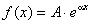 (A i a - дійсні числа)
(A i a - дійсні числа)
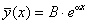 ,якщо a не є коренем характе-
ристичного рівняння(7.42);
,якщо a не є коренем характе-
ристичного рівняння(7.42);
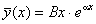 ,якщо a є однократним коренем;
,якщо a є однократним коренем;
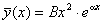 , якщо a є двократним коренем
(В – число, яке треба обчислити)
, якщо a є двократним коренем
(В – число, яке треба обчислити)
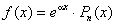 [a - дійсне число,
[a - дійсне число, 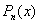 - многочлен n-го степеня]
- многочлен n-го степеня]
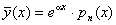 ,якщо a не є коренем характеристичного рівняння (7.42);
,якщо a не є коренем характеристичного рівняння (7.42);
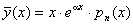 , якщо a є однократним коренем;
, якщо a є однократним коренем;
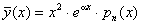 ,якщо a є двократним коренем[
,якщо a є двократним коренем[ 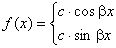 (с і
(с і 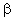 - дійсні числа)
- дійсні числа)
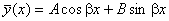 ,
якщо
,
якщо 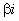 не є коренем
характеристичного рівняння
(7.42);
не є коренем
характеристичного рівняння
(7.42);
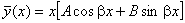 ,
якщо
,
якщо 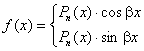 [
[ 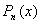 -многочлен n-го степеня]
-многочлен n-го степеня]
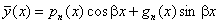 ,
якщо
,
якщо 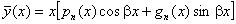 ,
якщо
,
якщо 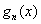 – многочлени
n-го порядку, коефіцієнти
яких треба обчислити ]
– многочлени
n-го порядку, коефіцієнти
яких треба обчислити ]
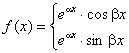 (a і
(a і 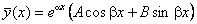 ,
якщо
,
якщо 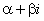 не є коренем
характеристичного рівняння
(6.42);
не є коренем
характеристичного рівняння
(6.42);
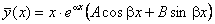 ,
якщо
,
якщо 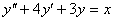 .
.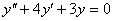 .
. має корені
має корені 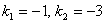 . Тому загальний розв’язок однорідного рівняння записуємо у вигляді
. Тому загальний розв’язок однорідного рівняння записуємо у вигляді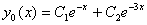 .
.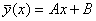 .
.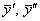 і підставимо їх у вхідне рівняння:
і підставимо їх у вхідне рівняння: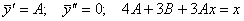 .
.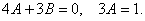
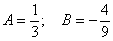 .
.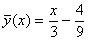 .
.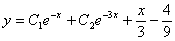
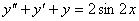 .
. ;
;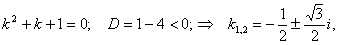
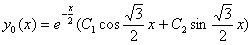 .
.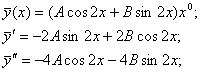
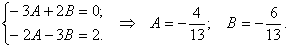
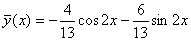
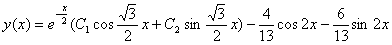 .
.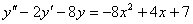 (Відп.
(Відп. 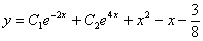 )
)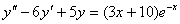 (Відп.
(Відп. 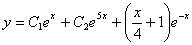 )
)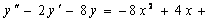 (Відп.
(Відп. 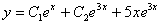 )
)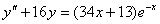 (Відп.
(Відп. 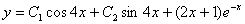 )
)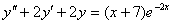 (Відп.
(Відп.  )
) (Відп.
(Відп. 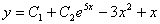 )
)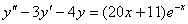 (Відп.
(Відп. 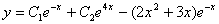 )
)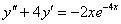 (Відп.
(Відп. 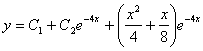 )
)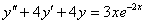 (Відп.
(Відп. 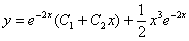 )
)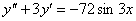 (Відп.
(Відп.  )
)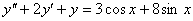 (Відп.
(Відп. 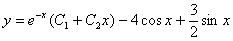 )
)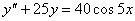 (Відп.
(Відп. 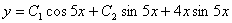 )
)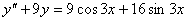 (Відп.
(Відп.