Диференціальне рівняння називають рівнянням з відокремлюваними змінними, якщо його права частина є добутком двох функцій, одна з яких залежить лише від аргумента х, а друга – лише від самої невідомої у:
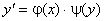 , (7.6)
, (7.6)
Тут ми вважаємо, що функція 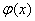 означена і неперервна для всіх
означена і неперервна для всіх 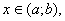 а функція
а функція 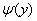 означена, неперервна і не рівна нулю для всіх
означена, неперервна і не рівна нулю для всіх 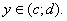
Позначимо 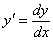 ; домножимо обидві частини рівняння (7.6) на dx і поділимо на
; домножимо обидві частини рівняння (7.6) на dx і поділимо на 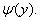 Рівняння прийме вигляд
Рівняння прийме вигляд
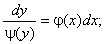 (7.7)
(7.7)
В так одержаному рівнянні змінні відокремлені: в ліву частину віднесено члени, які містять у і dy, в праву – члени, які містять х і dx.
Безпосередньо (диференціюванням !) встановлюється, що загальним інтегралом рівняння (7.7) є співвідношення
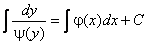 , (7.8)
, (7.8)
де С – довільна стала.
Приклад.
Зінтегрувати рівняння
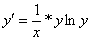 .
.
Розв’язання.Це рівняння з відокремлюваними змінними. Позначимо 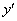 =
= 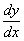 ; домножимо обидві частини рівняння на
; домножимо обидві частини рівняння на 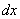 і розділимо на
і розділимо на 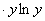 . Дістанемо рівняння, в якому змінні відокремлені
. Дістанемо рівняння, в якому змінні відокремлені
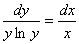 .
.
Після обчислення інтегралів, маємо
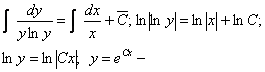
-загальний розв’язок рівняння.
Зауваження.Рівняння з відокремлюваними змінними можна також задати в симетричній відносно х і у диференціальній формі
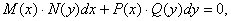 (7.9)
(7.9)
де функції 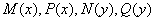 неперервні відповідно в інтервалах
неперервні відповідно в інтервалах 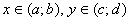 .
.
Для знаходження всіх розв’язків такого рівняння ділять обидві його частини на добуток 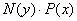
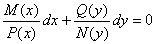 , (7.10)
, (7.10)
і інтегрують одержане так співвідношення 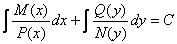 (7.11)
(7.11)
Якщо для 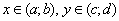 функції
функції 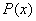 і
і 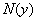 відмінні від нуля, то співвідношення (7.11) є загальним інтегралом рівняння (7.9).
відмінні від нуля, то співвідношення (7.11) є загальним інтегралом рівняння (7.9).
Приклад.
Зінтегрувати рівняння
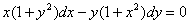
Розв’язання. Відокремимо змінні (поділимо обидві частини рівняння на 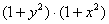 ):
):
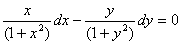
Інтегруючи кожен із доданків ( для цього не обов’язково один із них переносити у праву частину), прирівнюємо суму первісних постійній, яку позначаємо через 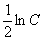 , маємо:
, маємо:
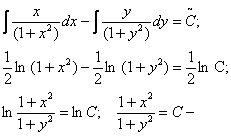 - загальний інтеграл рівняння
- загальний інтеграл рівняння


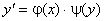 , (7.6)
, (7.6)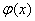 означена і неперервна для всіх
означена і неперервна для всіх 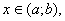 а функція
а функція 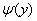 означена, неперервна і не рівна нулю для всіх
означена, неперервна і не рівна нулю для всіх 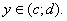
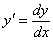 ; домножимо обидві частини рівняння (7.6) на dx і поділимо на
; домножимо обидві частини рівняння (7.6) на dx і поділимо на 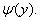 Рівняння прийме вигляд
Рівняння прийме вигляд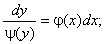 (7.7)
(7.7)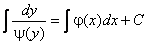 , (7.8)
, (7.8)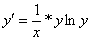 .
.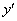 =
= 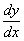 ; домножимо обидві частини рівняння на
; домножимо обидві частини рівняння на 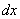 і розділимо на
і розділимо на 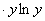 . Дістанемо рівняння, в якому змінні відокремлені
. Дістанемо рівняння, в якому змінні відокремлені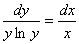 .
.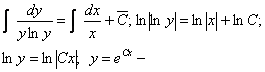
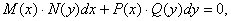 (7.9)
(7.9)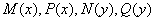 неперервні відповідно в інтервалах
неперервні відповідно в інтервалах 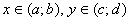 .
.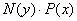
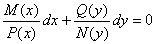 , (7.10)
, (7.10)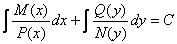 (7.11)
(7.11)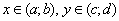 функції
функції 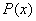 і
і 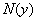 відмінні від нуля, то співвідношення (7.11) є загальним інтегралом рівняння (7.9).
відмінні від нуля, то співвідношення (7.11) є загальним інтегралом рівняння (7.9).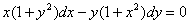
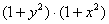 ):
):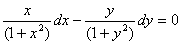
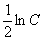 , маємо:
, маємо: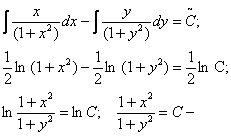 - загальний інтеграл рівняння
- загальний інтеграл рівняння