Обчислення інтеграла
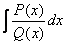
від правильного алгебраїчного дробу зводиться до інтегрування функції, що є скінченою сумою простих алгебраїчних дробів чотирьох типів:
1. 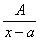 ; 2.
; 2. 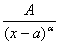 ,
,
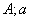 - дійсні числа;
- дійсні числа; 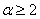 - ціле число.
- ціле число.
3. 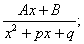 4.
4. 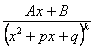 ,
,
А, В, p, q – дійсні числа, 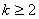 - ціле число,
- ціле число, 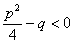 .
.
Вигляд простих алгебраїчних дробів визначається коренями знаменника 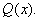
Тут можливі такі випадки.
Випадок перший. Корені многочлена Q(x) дійсні й різні: 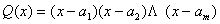 (6.17)
(6.17)
У цьому випадку правильний алгебраїчний дріб можна зобразити у вигляді суми простих алгебраїчних дробів першого типу
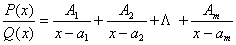 , (6.18) де
, (6.18) де 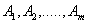 - деякі числа (невизначені коефіцієнти)
- деякі числа (невизначені коефіцієнти)
Отже,
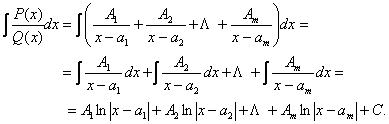
Приклад
Обчислити інтеграл
І = 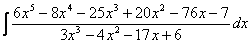 .
.
Розв’язання. Дріб
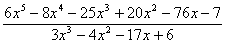
- неправильний. Виділяємо цілу частину
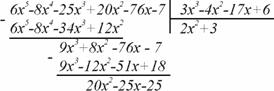
Заданий дріб набуває вигляду
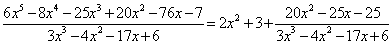
Тоді
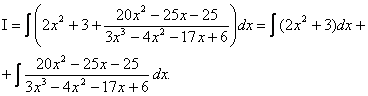
Інтеграл
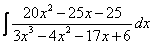
береться від правильного алгебраїчного дробу. Випишемо цей дріб окремо
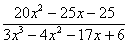 .
.
Знаменник дробу розкладемо на прості множники
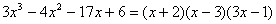 .
.
Тоді дріб подамо у вигляді суми простих алгебраїчних дробів
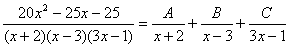 .
.
Зводимо дроби правої частини до спільного знаменника, ним є многочлен 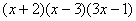 . Відкидаючи спільний знаменник в обох частинах, маємо
. Відкидаючи спільний знаменник в обох частинах, маємо
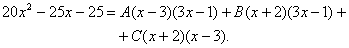
Для визначення коефіцієнтів будемо надавати х довільних значень (стільки, скільки невідомих). Дістанемо систему лінійних алгебраїчних рінянь, з якої і визначаються шукані коефіцієнти. Очевидно, що х доцільно надавати значень, які є коренями многочлена в знаменнику. Тоді кожного разу утворюється рівняння з одним невідомим.
Підставимо в рівність 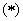 замість х послідовно числа
замість х послідовно числа 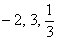 . Матимемо
. Матимемо
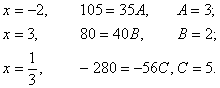
Описаний тут спосіб знаходження невідомих коефіцієнтів називають методом частинних значень.
Знаходимо інтеграл
 Отже, шуканий інтеграл дорівнює
Отже, шуканий інтеграл дорівнює
І= 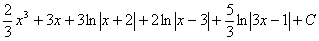 .
.
Випадок другий. Корені многочлена 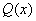 дісні і при цьому деякі з них кратні
дісні і при цьому деякі з них кратні 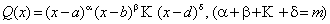 (6.19)
(6.19)
В цьому випадку дріб розкладається на прості дроби першого і другого типів:

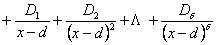 (6.20)
(6.20)
Приклад.
Обчислити інтеграл
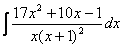
Розв’язання. Дріб
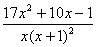
- правильний, причому знаменник уже розкладено на прості множники. Цей дріб через прості дроби записується так:
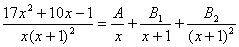
Зводимо дроби правої частини до спільного знаменника
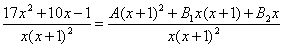
Відкидаючи спільний знаменник в обох частинах, маємо
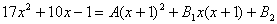
Записавши многочлен, який стоїть у правій частині цієї рівності за спадаючими степенями х, дістаємо
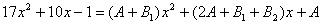 .
.
Прирівнюючи тепер коефіцієнти при 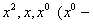 вільний член), матимемо таку систему 3-х лінійних алгебраїчних рівнянь з трьома невідомими:
вільний член), матимемо таку систему 3-х лінійних алгебраїчних рівнянь з трьома невідомими:
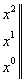
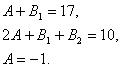
Розв'язуючи цю систему, маємо
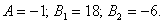
Тоді задана підінтегральна функція виразиться через прості дроби так:
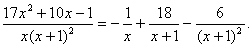
Описаний спосіб обчислення невідомих коефіцієнтів у розкладі дробу називають методом невизначених коефіцієнтів.
Отже,

Випадок третій. Серед коренів многочлена 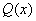 є прості комплексні корені:
є прості комплексні корені:
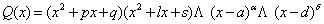 (6.21)
(6.21)
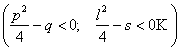 .
.
В цьому випадку дріб розкладається на прості дроби першого, другого і третього типів
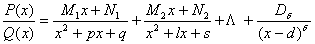 (6.22)
(6.22)
Приклад.
Обчислити інтеграл
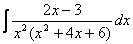 .
.
Розв’язання. Дискримінант квадратного тричлена від’ємний: 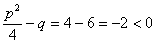 . Заданий дріб через прості алгебраїчні дроби записується так:
. Заданий дріб через прості алгебраїчні дроби записується так:
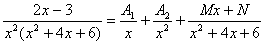 .
.
Звідси дістанемо таку тотожність:
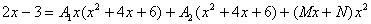
Прирівнюючи коефіцієнти при однакових степенях х, маємо таку систему рівнянь:
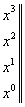
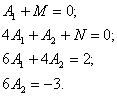
Звідси
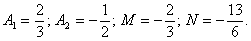
Отже,

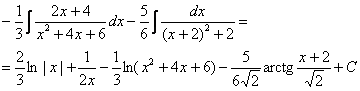
Випадок четвертий. Серед коренів многочлена 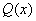 є кратні комплексні корені:
є кратні комплексні корені:
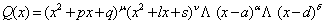 (6.23)
(6.23)
Тоді дріб розкладається на прості дроби всіх чотирьох типів.


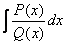
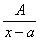 ; 2.
; 2. 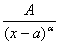 ,
,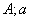 - дійсні числа;
- дійсні числа; 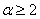 - ціле число.
- ціле число.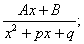 4.
4. 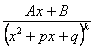 ,
,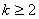 - ціле число,
- ціле число, 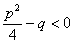 .
.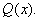
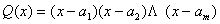 (6.17)
(6.17)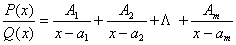 , (6.18) де
, (6.18) де 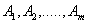 - деякі числа (невизначені коефіцієнти)
- деякі числа (невизначені коефіцієнти)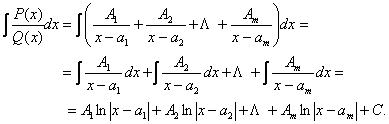
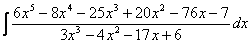 .
.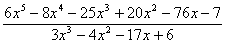
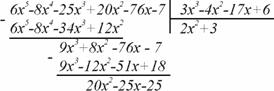
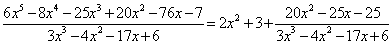
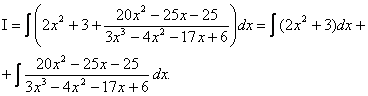
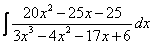
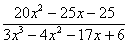 .
.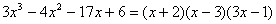 .
.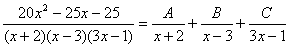 .
.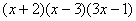 . Відкидаючи спільний знаменник в обох частинах, маємо
. Відкидаючи спільний знаменник в обох частинах, маємо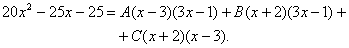
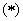
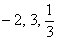 . Матимемо
. Матимемо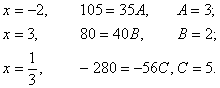
 Отже, шуканий інтеграл дорівнює
Отже, шуканий інтеграл дорівнює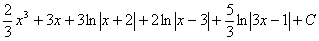 .
.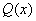 дісні і при цьому деякі з них кратні
дісні і при цьому деякі з них кратні 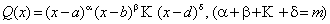 (6.19)
(6.19)
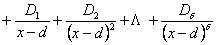 (6.20)
(6.20)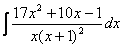
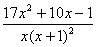
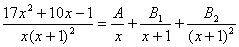
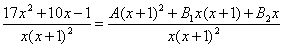
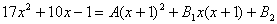
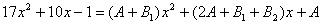 .
.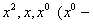 вільний член), матимемо таку систему 3-х лінійних алгебраїчних рівнянь з трьома невідомими:
вільний член), матимемо таку систему 3-х лінійних алгебраїчних рівнянь з трьома невідомими: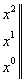
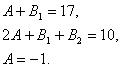
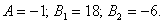
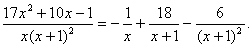

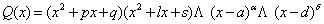 (6.21)
(6.21)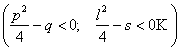 .
.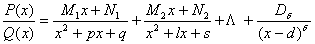 (6.22)
(6.22)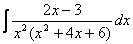 .
.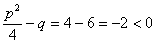 . Заданий дріб через прості алгебраїчні дроби записується так:
. Заданий дріб через прості алгебраїчні дроби записується так: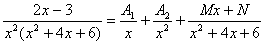 .
.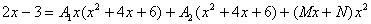
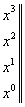
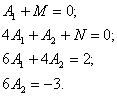
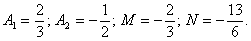

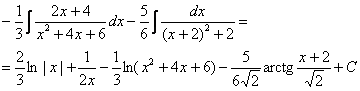
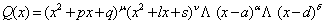 (6.23)
(6.23)