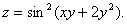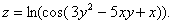Якщо функція 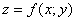 диференційовна в точці
диференційовна в точці 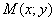 , то її повний приріст у цій точці
, то її повний приріст у цій точці
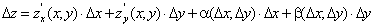 ,
,
де 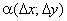 та
та 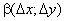 - нескінченно малі функції при
- нескінченно малі функції при 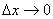 ,
, 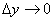 .
.
Означення 5.7. Головна, лінійна відносно приростів 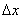 та
та 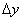 частина повного приросту функції
частина повного приросту функції 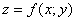 у точці
у точці 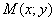 називається диференціалом цієї функції в точці М:
називається диференціалом цієї функції в точці М:
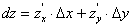
Диференціалами незалежних змінних х та у назвемо їх прирости: 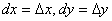 . Тоді повний диференціал запишемо у вигляді
. Тоді повний диференціал запишемо у вигляді
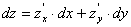
Вирази 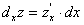 та
та 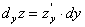 називають частинними дифереціалами функції
називають частинними дифереціалами функції 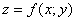 по х та у відповідно. Отже,
по х та у відповідно. Отже,
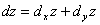
Приклад.
Знайти повний диференціал функції 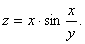
Розв’язання. Знайдемо частинні похідні:
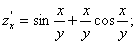
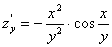
Згідно з формулою (5.11) дістанемо
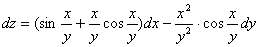
Розглянемо застосування повного диференціала в наближених обчисленнях.
Якщо функція 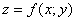 диференційована в точці
диференційована в точці 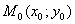 , то
, то
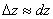
Звідки
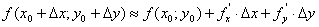
Цю формулу використовують в наближених обчисленнях.
Приклад 1. Обчислити наближено (1,04)2,02.
Розв’язання. Розглянемо функцію 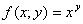 та знайдемо її частинні похідні
та знайдемо її частинні похідні
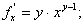
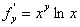 .
.
Виберемо х0=1, у0=2, тоді 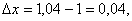
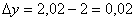 .
.
Знаходимо
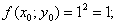
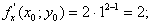
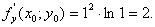
За формулою (4.13) дістанемо
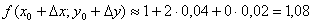
Отже, (1,04)2,02 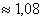 .
.
Розглянемо ще застосування повного диференціала для оцінки похибки при наближених обчисленнях.
Якщо максимальні похибки в знаходженні приросту функції та незалежних змінних позначити відповідно 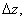
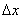 ,
, 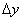 , то для оцінки похибки наближених обчислень маємо формулу
, то для оцінки похибки наближених обчислень маємо формулу
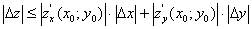
Приклад 2. Гіпотенуза прямокутного трикутника 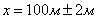 , а гострий кут
, а гострий кут 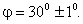 З якою точністю можна знайти протилежний цьому кутові катет?
З якою точністю можна знайти протилежний цьому кутові катет?
Розв’язання. Довжину катета позначимо через z. Тоді
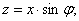
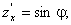
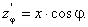
Виберемо 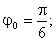
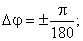 х=100;
х=100; 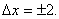
Тоді
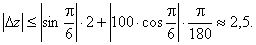
Вправи
Обчислити dz та d2z функцій
1. 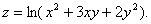
2. 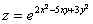 .
.
3. 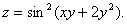
4. 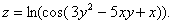


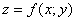 диференційовна в точці
диференційовна в точці 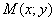 , то її повний приріст у цій точці
, то її повний приріст у цій точці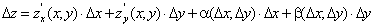 ,
,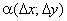 та
та 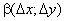 - нескінченно малі функції при
- нескінченно малі функції при 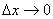 ,
, 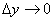 .
.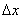 та
та 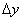 частина повного приросту функції
частина повного приросту функції 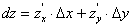
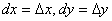 . Тоді повний диференціал запишемо у вигляді
. Тоді повний диференціал запишемо у вигляді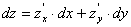
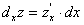 та
та 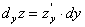 називають частинними дифереціалами функції
називають частинними дифереціалами функції 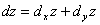
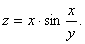
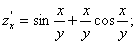
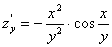
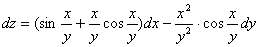
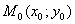 , то
, то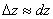
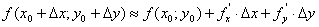
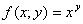 та знайдемо її частинні похідні
та знайдемо її частинні похідні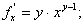
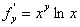 .
.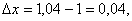
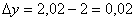 .
.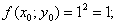
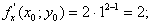
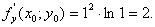
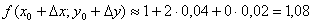
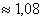 .
.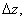
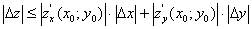
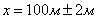 , а гострий кут
, а гострий кут 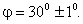 З якою точністю можна знайти протилежний цьому кутові катет?
З якою точністю можна знайти протилежний цьому кутові катет?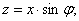
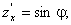
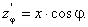
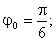
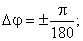 х=100;
х=100; 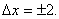
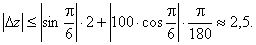
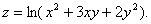
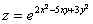 .
.