При дослідженні функцій виникає необхідність знаходити границі дробу 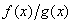 , чисельник і знаменник якого при
, чисельник і знаменник якого при 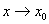 прямують до нуля або до безмежності. Знаходження таких границь називають розкриттям невизначеностей. Найбільш простим і ефективним методом розкриття невизначеностей є правила Лопіталя.
прямують до нуля або до безмежності. Знаходження таких границь називають розкриттям невизначеностей. Найбільш простим і ефективним методом розкриття невизначеностей є правила Лопіталя.
Теорема 1. (перше правило Лопіталя). Нехай для функцій  і
і 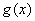 виконуються умови:
виконуються умови:
1) функції визначені в інтервалі 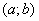 і при цьому
і при цьому
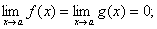
2) 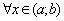
 і
і 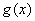 диференційовні, причому
диференційовні, причому 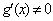 ;
;
3) існує (скінченна або нескінченна) границя
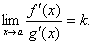
Тоді існує границя відношення 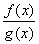 при
при 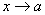 і
і
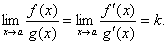
Доведення. Для 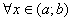 функції
функції  і
і 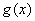 є диференційовні. Отже, дані функції в цьому інтервалі неперервні. Довизначимо функції
є диференційовні. Отже, дані функції в цьому інтервалі неперервні. Довизначимо функції  і
і 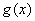 в точці
в точці 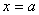 так
так
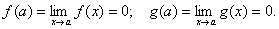
Отже, тепер  і
і 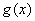 є неперервними на будь-якому відрізку
є неперервними на будь-якому відрізку 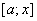 , де
, де 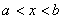 . Тому до функцій
. Тому до функцій  і
і 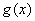 можна застосувати теорему Коші на відрізку
можна застосувати теорему Коші на відрізку 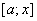
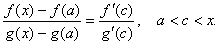
Якщо тепер 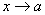 , то й
, то й 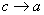 і з попередньої рівності дістаємо
і з попередньої рівності дістаємо
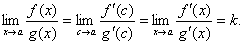
Теорему доведено.
Приклад. Знайти
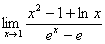 .
.
Розв’язання.
Нехай

Отже,
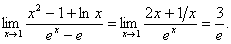
Може статися, що поряд з рівностями
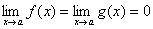
виконуються також рівності
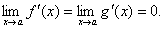
Тоді
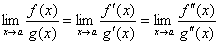 .
.
Взагалі, при виконанні відповідних умов цю процедуру можна застосовувати кілька разів.
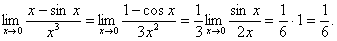
Вправи
Знайти границі функцій
1. 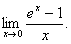 (Відп. 1)
(Відп. 1)
2. 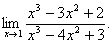 (Відп.
(Відп. 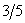 )
)
3. 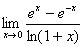 (Відп. 2)
(Відп. 2)
4. 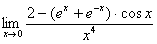 . (Відп.
. (Відп. 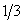 )
)
5. 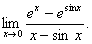 (Відп. 1)
(Відп. 1)
При розкритті невизначеностей типу 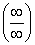 діє теорема, яку наводимо без доведення.
діє теорема, яку наводимо без доведення.
Теорема 2 (друге правило Лопіталя). Нехай для функцій  і
і 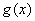 виконуються умови:
виконуються умови:
1. Функції визначені в інтервалі 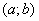 , і при цьому
, і при цьому
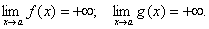
2. Функції диференційовні в інтервалі 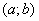 , причому
, причому
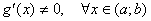 .
.
3. Існує (скінченна або нескінченна) границя
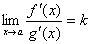 .
.
Тоді й
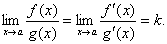
Приклад. Знайти
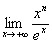 .
.
Розв’язання. 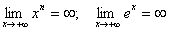 ..
..
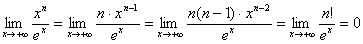 .
.
Вправи
Знайти границі функцій:
1. 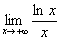 (Відп. 0)
(Відп. 0)
2. 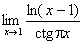 . (Відп. 0)
. (Відп. 0)
3. 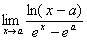 . (Відп. 1)
. (Відп. 1)
4. 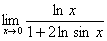 . (Відп.
. (Відп. 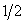 )
)
Зробимо ще таке зауваження. За допомогою тотожних перетворень до основних випадків 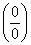 або
або 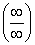 можна звести і невизначеності інших типів:
можна звести і невизначеності інших типів: 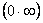 ;
; 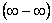 ;
; 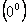 ;
; 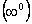 ;
;  .
.
Справді, нехай маємо невизначеність 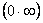 :
:
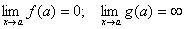 .
.
Тоді
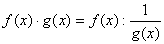 .
.
Дістали невизначеність 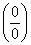 .
.
Приклад. Знайти
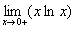 .
.
Розв’язання. 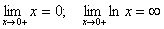 .
.
Але
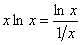 .
.
Маємо
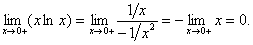
Якщо маємо невизначеність 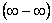 :
:
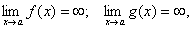
то різницю 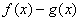 можна записати
можна записати
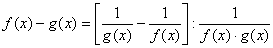 .
.
Дістали невизначеність виду 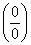 .
.
Приклад. Знайти
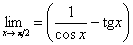 .
.
Розв'язання. 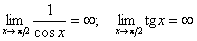 .
.
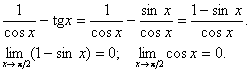
Отже,
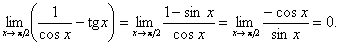
Якщо маємо степінь
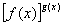
і 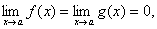
то використовуємо рівність
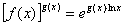
і справа зводиться до розкриття невизначеності вигляду 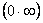 у показнику.
у показнику.
Аналогічно розкриваються невизначеності  ,
, 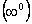 .
.
Приклад. Знайти
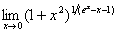 .
.
Розв’язання. 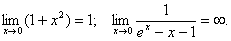
Отже,
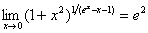 .
.
Вправи
Знайти границі функцій
1. 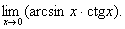 (Відп. 1)
(Відп. 1)
2. 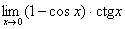 . (Відп. 0)
. (Відп. 0)
3. 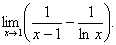 (Відп.
(Відп. 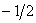 )
)
4. 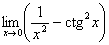 . (Відп.
. (Відп. 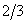 )
)
5. 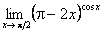 . (Відп. 1)
. (Відп. 1)
6. 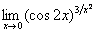 . (Відп.
. (Відп. 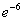 )
)
7. 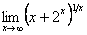 . (Відп. 2)
. (Відп. 2)
8. 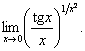 (Відп.
(Відп. 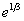 )
)


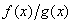 , чисельник і знаменник якого при
, чисельник і знаменник якого при 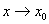 прямують до нуля або до безмежності. Знаходження таких границь називають розкриттям невизначеностей. Найбільш простим і ефективним методом розкриття невизначеностей є правила Лопіталя.
прямують до нуля або до безмежності. Знаходження таких границь називають розкриттям невизначеностей. Найбільш простим і ефективним методом розкриття невизначеностей є правила Лопіталя. і
і 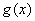 виконуються умови:
виконуються умови: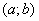 і при цьому
і при цьому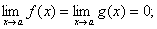
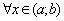
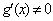 ;
;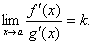
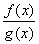 при
при 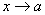 і
і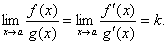
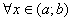 функції
функції 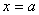 так
так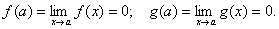
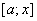 , де
, де 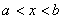 . Тому до функцій
. Тому до функцій 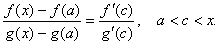
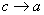 і з попередньої рівності дістаємо
і з попередньої рівності дістаємо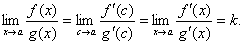
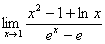 .
.
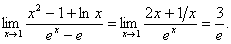
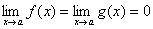
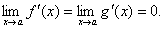
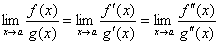 .
.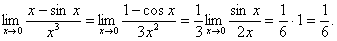
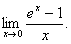 (Відп. 1)
(Відп. 1)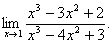 (Відп.
(Відп. 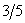 )
)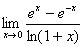 (Відп. 2)
(Відп. 2)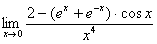 . (Відп.
. (Відп. 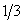 )
)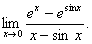 (Відп. 1)
(Відп. 1)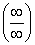 діє теорема, яку наводимо без доведення.
діє теорема, яку наводимо без доведення.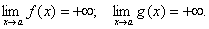
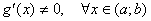 .
.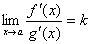 .
.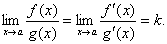
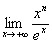 .
.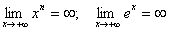 ..
..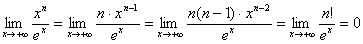 .
.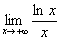 (Відп. 0)
(Відп. 0)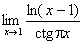 . (Відп. 0)
. (Відп. 0)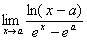 . (Відп. 1)
. (Відп. 1)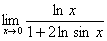 . (Відп.
. (Відп. 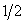 )
)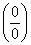 або
або 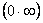 ;
; 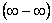 ;
; 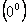 ;
; 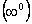 ;
;  .
.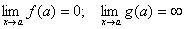 .
.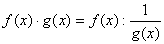 .
.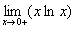 .
.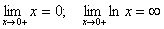 .
.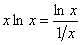 .
.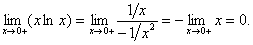
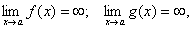
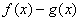 можна записати
можна записати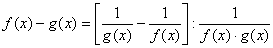 .
.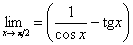 .
.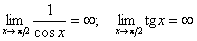 .
.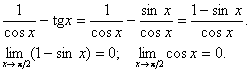
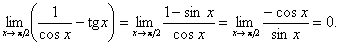
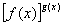
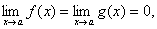
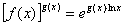
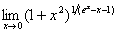 .
.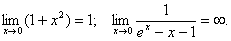
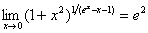 .
.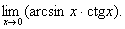 (Відп. 1)
(Відп. 1)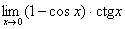 . (Відп. 0)
. (Відп. 0)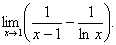 (Відп.
(Відп. 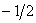 )
)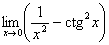 . (Відп.
. (Відп. 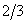 )
)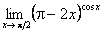 . (Відп. 1)
. (Відп. 1)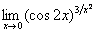 . (Відп.
. (Відп. 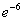 )
)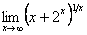 . (Відп. 2)
. (Відп. 2)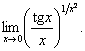 (Відп.
(Відп. 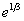 )
)