В усіх цих теоремах йдеться про те, що коли функція та її похідна першого порядку задовольняють певним умовам, то всередині інтервалу знайдеться точка, в якій функція має певні властивості (про ці властивості йдеться в теоремі). Тому й самі теореми називають теоремами про середнє.
Теорема Ролля. Нехай функція  задовольняє умовам:
задовольняє умовам:
1) визначена і неперервна на відрізку 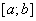 ;
;
2) диференційовна в інтервалі 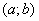 ;
;
3) на кінцях відрізку набуває однакових значень: 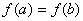 .
.
Тоді всередині інтервалу 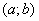 існує принаймні одна точка
існує принаймні одна точка 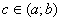 , в якій
, в якій 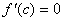 .
.
Доведення. Оскільки функція  за умовою теореми неперервна на відрізку
за умовою теореми неперервна на відрізку 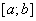 , то вона набуває на ньому найбільшого значення М і найменшого значення m.
, то вона набуває на ньому найбільшого значення М і найменшого значення m.
Якщо М=m, то 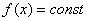 для
для 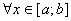 і тому за точку
і тому за точку 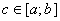 можна взяти будь-яку точку інтервалу
можна взяти будь-яку точку інтервалу 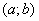 .
.
Якщо 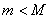 , а
, а 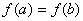 , то принаймні одне з значень m або М досягається у внутрішній точці відрізку
, то принаймні одне з значень m або М досягається у внутрішній точці відрізку 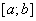 . Нехай, наприклад, в точці с функція
. Нехай, наприклад, в точці с функція  набуває найменшого значення:
набуває найменшого значення: 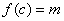 .
.
Покажемо, що 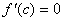 .
.
Справді, для досить малих 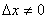 точка
точка 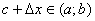 , причому
, причому
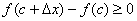 при
при 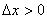 ,
,
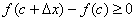 при
при 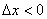 .
.
Тому
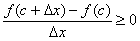 при
при 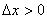 ,
,
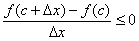 при
при 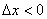 .
.
Границя відношень при 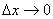 існує і дорівнює похідній
існує і дорівнює похідній 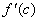 , тому
, тому
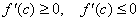 .
.
Звідси маємо, що 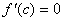 .
.
Теорему доведено.
Геометрично теорема Ролля означає, що серед усіх дотичних до графіка функції 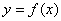 знайдеться принаймні одна, паралельна осі Ох.
знайдеться принаймні одна, паралельна осі Ох.
Теорема Лагранжа. Якщо функція  :
:
1) задана і неперервна на відрізку 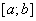 ;
;
2) диференційовна в інтервалі 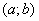 .
.
Тоді існує принаймні одна точка 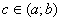 така, що
така, що
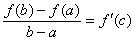 (4.25)
(4.25)
Доведення. Розглянемо допоміжну функцію
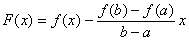 .
.
Функція 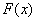 задовольняє всі умови теореми Ролля. Вона неперервна на відрізку
задовольняє всі умови теореми Ролля. Вона неперервна на відрізку 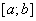 (як різниця двох неперервних функцій); диференційовна на
(як різниця двох неперервних функцій); диференційовна на 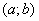 , причому
, причому
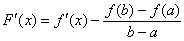 ;
;
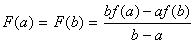 .
.
Отже, існує точка 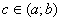 , в якій
, в якій 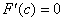 або, що те саме
або, що те саме
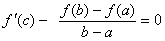 ,
,
звідки
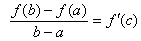 .
.
Теорему доведено.
Геометрично теорема Лагранжа означає, що серед усіх дотичних до графіка функції 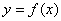 знайдеться принаймні одна, паралельна січній, яка проходить через точки
знайдеться принаймні одна, паралельна січній, яка проходить через точки 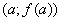 і
і 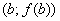 .
.
Зауваження. Рівність
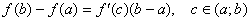
називається формулою Лагранжа. Її запишемо трохи інакше. Введемо позначення
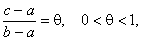
тоді
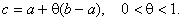
Тому
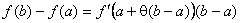 .
.
Покладаючи 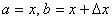 , матимемо
, матимемо
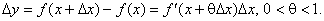 (4.26)
(4.26)
Формулу (4.26) називають формулою скінченних приростів.
Наслідок 1. Якщо функція  на проміжку
на проміжку 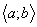 має похідну
має похідну 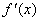 і
і 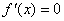 при будь-якому
при будь-якому 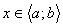 , то
, то  на даному проміжку є сталою.
на даному проміжку є сталою.
Наслідок 2. Якщо функції  і
і 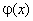 на проміжку
на проміжку 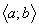 мають похідні
мають похідні 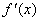 ,
, 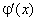 і при будь-якому
і при будь-якому 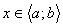
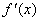 =
= 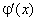 , то різниця між цими функціями
, то різниця між цими функціями 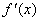 -
- 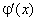 є величина стала.
є величина стала.
Теорема Коші. Нехай
1) функції  і
і 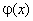 задані і неперервні на відрізку
задані і неперервні на відрізку 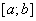 ;
;
2) диференційовні в інтервалі 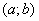 ;
;
3) похідна 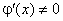 для
для 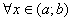 .
.
Тоді існує принаймні одна точка 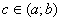 так, що
так, що
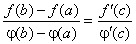 . (4.27)
. (4.27)
Доведення. Розглянемо на відрізку 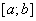 таку функцію
таку функцію
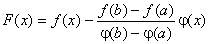 .
.
Цю функцію можна розглядати на відрізку 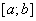 , бо
, бо 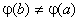 , оскільки у протилежному випадку для функції
, оскільки у протилежному випадку для функції 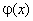 знайдеться принаймні одна точка
знайдеться принаймні одна точка 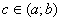 така, що
така, що 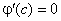 . А це суперечить умові, що
. А це суперечить умові, що 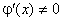 для
для 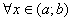 .
.
Функція 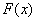 задовольняє всім умовам теореми Ролля. Тому існує принаймні одна точка
задовольняє всім умовам теореми Ролля. Тому існує принаймні одна точка 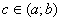 така, що
така, що 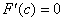 або, що те саме
або, що те саме
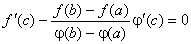 .
.
Звідси маємо
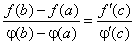 .
.


 задовольняє умовам:
задовольняє умовам: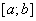 ;
;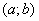 ;
;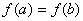 .
.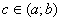 , в якій
, в якій 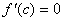 .
.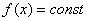 для
для 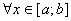 і тому за точку
і тому за точку 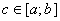 можна взяти будь-яку точку інтервалу
можна взяти будь-яку точку інтервалу 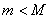 , а
, а 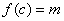 .
.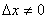 точка
точка 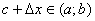 , причому
, причому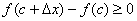 при
при 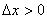 ,
,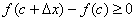 при
при 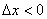 .
.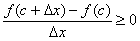 при
при 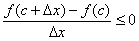 при
при 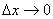 існує і дорівнює похідній
існує і дорівнює похідній 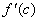 , тому
, тому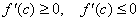 .
.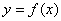 знайдеться принаймні одна, паралельна осі Ох.
знайдеться принаймні одна, паралельна осі Ох.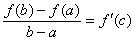 (4.25)
(4.25)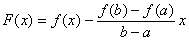 .
.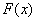 задовольняє всі умови теореми Ролля. Вона неперервна на відрізку
задовольняє всі умови теореми Ролля. Вона неперервна на відрізку 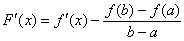 ;
;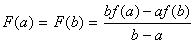 .
.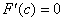 або, що те саме
або, що те саме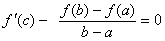 ,
,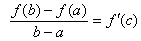 .
.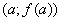 і
і 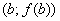 .
.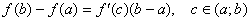
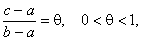
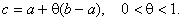
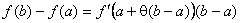 .
.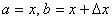 , матимемо
, матимемо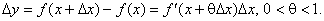 (4.26)
(4.26)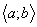 має похідну
має похідну 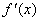 і
і 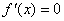 при будь-якому
при будь-якому 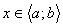 , то
, то 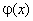 на проміжку
на проміжку 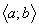 мають похідні
мають похідні 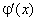 і при будь-якому
і при будь-якому 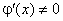 для
для 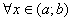 .
.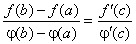 . (4.27)
. (4.27)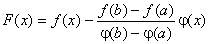 .
.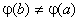 , оскільки у протилежному випадку для функції
, оскільки у протилежному випадку для функції 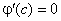 . А це суперечить умові, що
. А це суперечить умові, що 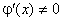 для
для 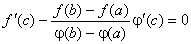 .
.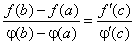 .
.