Залежно від того яка з умов неперервності не виконується, точки розриву поділяють на два роди.
Означення . Точка розриву 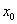 функції
функції  називається точкою розриву першого роду, якщо в цій точці існують скінченні лівостороння і правостороння границі. Якщо границі рівні між собою, то точка
називається точкою розриву першого роду, якщо в цій точці існують скінченні лівостороння і правостороння границі. Якщо границі рівні між собою, то точка 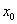 називається точкою поправного розриву.
називається точкою поправного розриву.
Точка розриву 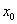 функції
функції  називається точкою розриву другого роду, якщо в ній не існує принаймні одна з односторонніх границь.
називається точкою розриву другого роду, якщо в ній не існує принаймні одна з односторонніх границь.
Приклади
Для даних функцій знайти точки розриву і визначити характер розриву:
1) 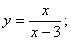 2)
2) 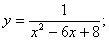 3)
3) 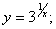 4)
4) 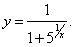
Розв’язання. 1) Дана функція визначена при всіх значеннях х, крім точки х=3. Для визначення характеру розриву знайдемо лівосторонню і правосторонню границі функції при 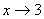 :
:
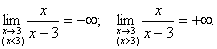
Отже, х=3 – точка розриву другого роду.
2) Точками розриву даної функції є точки х=2 та х=4, в яких знаменник дробу дорівнює нулю. Легко бачити, що в цих точках функція має нескінченні розриви, а звідси х=2 та х=4 – точки розриву другого роду.
3) Дана функція визначена при всіх значеннях х, крім х=0. Знайдемо лівосторонню і правосторонню границі функції при 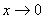 :
:
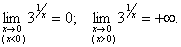
х=0 – точка розриву другого роду.
4) Для даної функції єдиною точкою розриву є точка х=0. Знайдемо односторонні границі цієї функції при 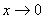 :
:
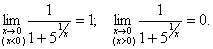 Оскільки лівостороння і правостороння границі даної функції при
Оскільки лівостороння і правостороння границі даної функції при 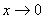 є скінченими, то х=0 – точка розриву першого роду.
є скінченими, то х=0 – точка розриву першого роду.


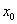 функції
функції  називається точкою розриву першого роду, якщо в цій точці існують скінченні лівостороння і правостороння границі. Якщо границі рівні між собою, то точка
називається точкою розриву першого роду, якщо в цій точці існують скінченні лівостороння і правостороння границі. Якщо границі рівні між собою, то точка 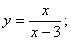 2)
2) 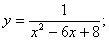 3)
3) 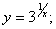 4)
4) 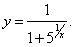
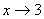 :
: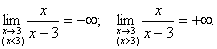
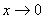 :
: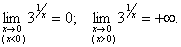
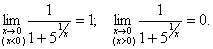 Оскільки лівостороння і правостороння границі даної функції при
Оскільки лівостороння і правостороння границі даної функції при