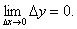Нехай функція 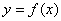 визначена в усіх точках деякого проміжку
визначена в усіх точках деякого проміжку 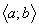 і нехай
і нехай 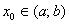 - довільна внутрішня точка цього проміжку.
- довільна внутрішня точка цього проміжку.
Означення .Функція 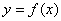 неперервною в точці
неперервною в точці 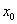 , якщо
, якщо 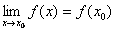 .
.
Звідси дістанемо необхідні та достатні умови того, щоб функція  була неперервною в точці
була неперервною в точці 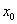 :
:
1) функція  визначена в точці
визначена в точці 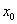 ;
;
2) існує лівостороння границя функції в точці – число 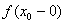 ;
;
3) існує правостороння границя функції в точці – число 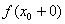 ;
;
4) лівостороння і правостороння границі рівні
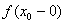 =
= 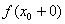 ;
;
5) лівостороння і правостороння границі в точці 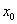 дорівнюють значенню функції в цій точці
дорівнюють значенню функції в цій точці
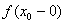 =
= 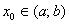 .
.
Якщо хоч одна з цих умов не виконується в точці 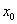 , то функція в цій точці називається розривною, а сама точка
, то функція в цій точці називається розривною, а сама точка 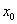 називається точкою розриву функції.
називається точкою розриву функції.
Використавши означення границі функції в точці, можна дати таке означення неперервності функції в точці.
Означення .Функція 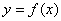 називається неперервною в точці
називається неперервною в точці 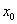 , якщо для будь якого як завгодно малого числа
, якщо для будь якого як завгодно малого числа 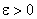 існує таке число
існує таке число 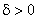 , що для всіх
, що для всіх 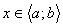 ,, які задовольняють неревність
,, які задовольняють неревність 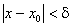 виконується нерівність
виконується нерівність 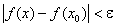 .
.
Зауваження. На практиці при дослідженні функцій на неперервність найчастіше користуються означенням неперервності функції, яке базується на понятті приросту функції в точці.
Нехай функція 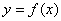 визначена в усіх точках деякого проміжку
визначена в усіх точках деякого проміжку 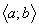 . Візьмемо дві довільні точки з цього проміжку
. Візьмемо дві довільні точки з цього проміжку 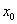 і
і 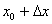 , де
, де 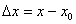 .
.
Тоді число 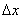 називається приростом аргументу, а число
називається приростом аргументу, а число 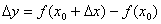 - приростом функції
- приростом функції  в точці
в точці 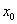 .
.
Означення .Функція 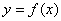 називається неперервною в точці
називається неперервною в точці 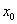 , якщо
, якщо
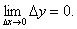


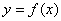 визначена в усіх точках деякого проміжку
визначена в усіх точках деякого проміжку 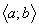 і нехай
і нехай 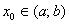 - довільна внутрішня точка цього проміжку.
- довільна внутрішня точка цього проміжку.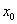 , якщо
, якщо 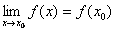 .
. була неперервною в точці
була неперервною в точці 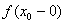 ;
;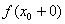 ;
;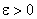 існує таке число
існує таке число 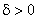 , що для всіх
, що для всіх 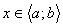 ,, які задовольняють неревність
,, які задовольняють неревність 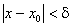 виконується нерівність
виконується нерівність 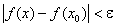 .
.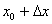 , де
, де 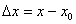 .
.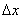 називається приростом аргументу, а число
називається приростом аргументу, а число 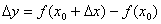 - приростом функції
- приростом функції