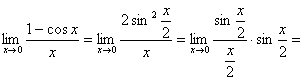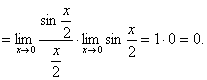Мови програмуванняВідео уроки php mysqlПаскальСіАсемблерJavaMatlabPhpHtmlJavaScriptCSSC#DelphiТурбо Пролог1С Компьютерные сетиСистемное программное обеспечениеИнформационные технологииПрограммирование Linux
Unix
Алгоритмічні мови
Архітектура мікроконтролерів
Введення в розробку розподілених інформаційних систем
Дискретна математика
Інформаційне обслуговування користувачів
Інформація та моделювання в управлінні виробництвом
Комп'ютерна графіка
Лекції
|
Перша особлива границяДата додавання: 2015-01-08; переглядів: 1283.
|
Онлайн система числення Калькулятор онлайн звичайний Науковий калькулятор онлайн
| ||||||||||||||||

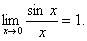
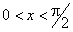 ). Проведемо хорду АМ і дотичну AN, що перетинає продовження радіуса ОМ у точці N.
). Проведемо хорду АМ і дотичну AN, що перетинає продовження радіуса ОМ у точці N.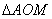 < площі сектора АОМ < площі
< площі сектора АОМ < площі 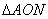 ,
,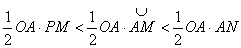 .
.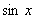 , AN=tg x,
, AN=tg x, 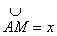 , то останні нерівності набувають вигляду:
, то останні нерівності набувають вигляду: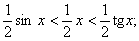
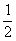 маємо:
маємо: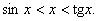
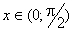
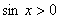 , поділимо ці нерівності на sinx. Знайдемо
, поділимо ці нерівності на sinx. Знайдемо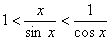 ,
,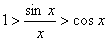 ;
;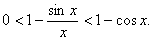
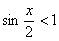 , то
, то 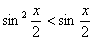 , а тому при
, а тому при 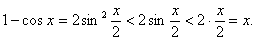
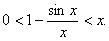
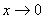 , дістанемо
, дістанемо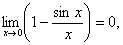
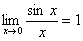 .
.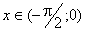 . Введемо нову змінну
. Введемо нову змінну 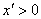 за формулою
за формулою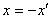 .
.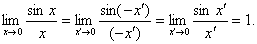
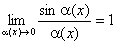 .
.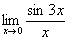 .
.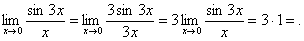
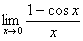 .
.