Нехай функція y = f(x) визначена на проміжку <a;b> крім, можливо, точки 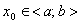 .
.
Означення . функція y = f(x) називається нескінченно малою в точці x0, якщо
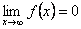 .
.
Функція y = f(x) називається нескінченно великою в точці x0, якщо
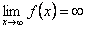 .
.
Властивості нескінченно малих та нескінченно великих функцій подамо у вигляді теорем.
Теорема. Для того щоб
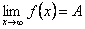
необхідно і достатньо, щоб функція
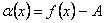
була нескінченно малою в точці x0.
Доведення. Необхідність. Нехай 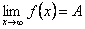 .
.
Тоді.
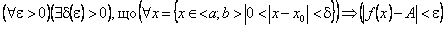 Позначивши
Позначивши 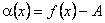 , дістанемо, що
, дістанемо, що 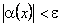 .
.
Достатність. Нехай 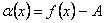 є нескінченно малою в точці x0 :
є нескінченно малою в точці x0 : 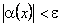 , або, що те саме
, або, що те саме 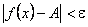 . Отже, тоді А є границею функції f(x) у точці x0.
. Отже, тоді А є границею функції f(x) у точці x0.
Теорему доведено.
Теорема. Алгебраїчна сума і добуток скінченого числа нескінченно малих функцій в точці x0, а також добуток нескінченно малої функції на функцію обмежену є функція нескінченно мала в точці x0.
Доведення. Для простоти припустимо, що маємо дві нескінченно малі функції 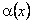 i
i 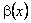 та покажемо, що функція
та покажемо, що функція 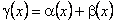 є також нескінченно мала функція. Для цього задамо довільне число
є також нескінченно мала функція. Для цього задамо довільне число 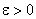 . Тоді, оскільки
. Тоді, оскільки 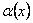 є нескінченно мала функція в точці x0, то для числа
є нескінченно мала функція в точці x0, то для числа 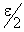 існує таке число
існує таке число 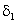 , що для всіх
, що для всіх 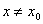 , які задовольняють нерівність
, які задовольняють нерівність 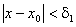 , виконується нерівність
, виконується нерівність 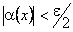 . Існує також число
. Існує також число 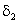 що для
що для 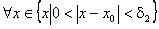 виконується нерівність
виконується нерівність 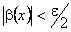 . Візьмемо тепер
. Візьмемо тепер 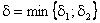 . Тоді
. Тоді 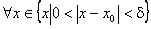 одночасно виконуються обидві нерівності
одночасно виконуються обидві нерівності 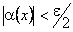 та
та 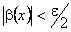 . Використавши тепер властивості модуля суми, дістанемо :
. Використавши тепер властивості модуля суми, дістанемо :
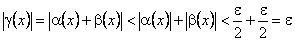 .
.
Використувавши метод математичної індукції, можна довести справедливість цієї властивості і для будь-якого (певного) числа нескінченно малих функцій. Одну частину теореми доведемо.
Такі самі міркування доводять решту властивостей.
Теорема. Якщо 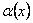 - нескінченно мала в точці x0 і
- нескінченно мала в точці x0 і 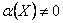 в околі точки x0, то функція
в околі точки x0, то функція 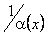 є нескінченно велика в цій точці. Якщо f(x) – нескінченно велика в точці x0, то функція
є нескінченно велика в цій точці. Якщо f(x) – нескінченно велика в точці x0, то функція 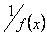 - нескінченно мала в цій точці.
- нескінченно мала в цій точці.
Доведення. Нехай 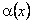 - нескінченно мала в точці x0. Візьмемо довільне число N>0. Тоді для числа
- нескінченно мала в точці x0. Візьмемо довільне число N>0. Тоді для числа 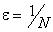 існує таке число
існує таке число 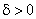 , що
, що 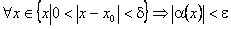 .
.
Не зменшуючи загальності, можна припустити, що 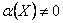 для всіх x, які задовольняють нерівність
для всіх x, які задовольняють нерівність 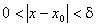 . Тоді для цих значень x можна розглядати функцію
. Тоді для цих значень x можна розглядати функцію 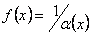 , яка задовольняє нерівність
, яка задовольняє нерівність
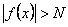 .
.
Першу частину теореми доведено. Друга частина теореми доводиться аналогічно.
Іноді доводиться розглядати не одну, а кілька нескінченно малих функцій у даній точці. Такі функції порівнюють між собою за допомогою границі їх відношення.
Означення Нехай функції 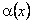 i
i 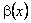 нескінченно малі в точці x0. Тоді :
нескінченно малі в точці x0. Тоді :
1) якщо 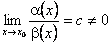 , то
, то 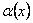 i
i 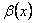 називаються нескінченно малими однакового порядку малості в точці x0.
називаються нескінченно малими однакового порядку малості в точці x0.
2) якщо 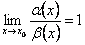 , то
, то 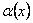 i
i 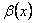 називаються еквівалентними в точці x0, і записують
називаються еквівалентними в точці x0, і записують 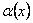 ~
~ 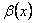 .
.
3) якщо 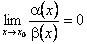 , то
, то 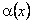 називається нескінченно малою вищого порядку порівняно з
називається нескінченно малою вищого порядку порівняно з 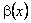 в точці x0. При цьому
в точці x0. При цьому 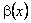 називається нескінченно малою нижчого порядку малості, ніж
називається нескінченно малою нижчого порядку малості, ніж 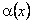 .
.
Насамкінець наводимо приклади еквівалентних нескінченно малих при 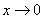 :
:
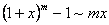 ;
; 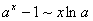 ;
; 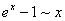 ;
; 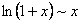 ;
; 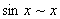 ;
; 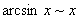 ;
; 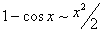 ;
; 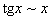 ;
; 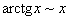 .
.


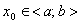 .
.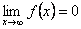 .
.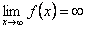 .
.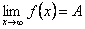
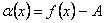
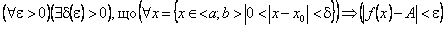 Позначивши
Позначивши 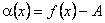 , дістанемо, що
, дістанемо, що 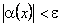 .
.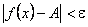 . Отже, тоді А є границею функції f(x) у точці x0.
. Отже, тоді А є границею функції f(x) у точці x0.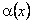 i
i 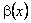 та покажемо, що функція
та покажемо, що функція 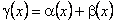 є також нескінченно мала функція. Для цього задамо довільне число
є також нескінченно мала функція. Для цього задамо довільне число 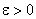 . Тоді, оскільки
. Тоді, оскільки 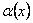 є нескінченно мала функція в точці x0, то для числа
є нескінченно мала функція в точці x0, то для числа 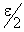 існує таке число
існує таке число 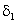 , що для всіх
, що для всіх 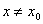 , які задовольняють нерівність
, які задовольняють нерівність 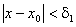 , виконується нерівність
, виконується нерівність 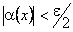 . Існує також число
. Існує також число 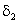 що для
що для 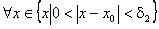 виконується нерівність
виконується нерівність 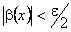 . Візьмемо тепер
. Візьмемо тепер 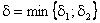 . Тоді
. Тоді 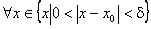 одночасно виконуються обидві нерівності
одночасно виконуються обидві нерівності 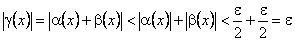 .
.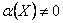 в околі точки x0, то функція
в околі точки x0, то функція 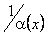 є нескінченно велика в цій точці. Якщо f(x) – нескінченно велика в точці x0, то функція
є нескінченно велика в цій точці. Якщо f(x) – нескінченно велика в точці x0, то функція 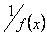 - нескінченно мала в цій точці.
- нескінченно мала в цій точці.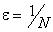 існує таке число
існує таке число 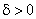 , що
, що 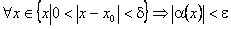 .
.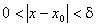 . Тоді для цих значень x можна розглядати функцію
. Тоді для цих значень x можна розглядати функцію 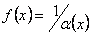 , яка задовольняє нерівність
, яка задовольняє нерівність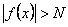 .
.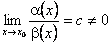 , то
, то 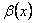 називаються нескінченно малими однакового порядку малості в точці x0.
називаються нескінченно малими однакового порядку малості в точці x0.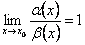 , то
, то 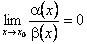 , то
, то 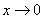 :
: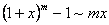 ;
; 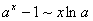 ;
; 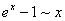 ;
; 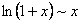 ;
; 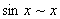 ;
; 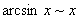 ;
; 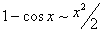 ;
; 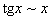 ;
; 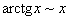 .
.