Нехай площина Q проходить через точку 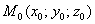 перпендикулярно вектору
перпендикулярно вектору 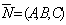 .
.
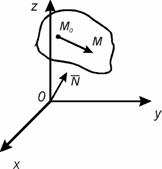
Цими умовами визначена єдина площина в просторі. Вектор 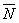 називають нормальним вектором площини. Позначимо через М(х;у;z) довільну точку площини.
називають нормальним вектором площини. Позначимо через М(х;у;z) довільну точку площини.
Вектор 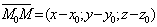 перпендикулярний до вектора
перпендикулярний до вектора 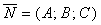 і їх скалярний добуток дорівнює нулю:
і їх скалярний добуток дорівнює нулю: 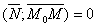 , або
, або
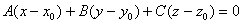 . (2.44)
. (2.44)
Це рівняння площини, яка проходить через задану точку М0 перпендикулярно до вектора 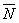 .
.
Рівняння площини
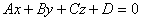 (2.45)
(2.45)
називають загальним рівнянням площини.
Доводиться, що будь-якому рівнянню першого степеня відносно змінних х, у, z відповідає площина (і лише площина) в просторі.
Умови паралельності і перпендикулярності площин 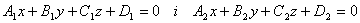 виписують з умов колінеарності й перпендикулярності їх нормальних векторів
виписують з умов колінеарності й перпендикулярності їх нормальних векторів 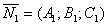 і
і 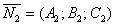 .
.
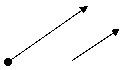 Нехай дано яку-небудь пряму L, що проходить через точку
Нехай дано яку-небудь пряму L, що проходить через точку 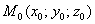 паралельно вектору
паралельно вектору 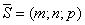 (називають напрямним вектором прямої). Позначимо через М(х,у,z) довільну точку прямої. З умов колінеарності векторів
(називають напрямним вектором прямої). Позначимо через М(х,у,z) довільну точку прямої. З умов колінеарності векторів 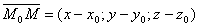 і
і 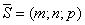 , маємо
, маємо
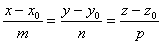 (2.46)
(2.46)
Це рівняння називають канонічним рівнянням прямої.
Вправи
1. Скласти рівняння площини, що проходить через точку М(2;3;5) перпендикулярно вектору 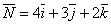 . (Відп.: 4х+3у+2z-27=0).
. (Відп.: 4х+3у+2z-27=0).
2. Скласти рівняння площини, що проходить через точку М(2;3;-1) паралельно площині 5х-3у+2z-10=0. (Відп.: 5х-3у+2z+1=0).
3. Написати рівняння прямої, яка проходить через точку М(5;3;4) паралельно вектору 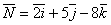 . (Відп.:
. (Відп.: 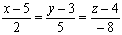 ).
).
4. Дано три послідовні вершини паралелограма А(3;0;-1), В(1;2;-4) і С(0;7;-2). Скласти рівняння сторін AD і CD. (Відп.: 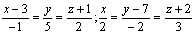 ).
).
Дано точки А(-1;2;3) і В(2;-3;1). Скласти рівняння прямої, яка проходить через точку М(3;-1;2) паралельно вектору 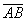 . (Відп.:
. (Відп.: 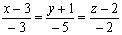 ).
).


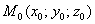 перпендикулярно вектору
перпендикулярно вектору 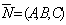 .
.
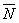 називають нормальним вектором площини. Позначимо через М(х;у;z) довільну точку площини.
називають нормальним вектором площини. Позначимо через М(х;у;z) довільну точку площини.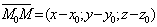 перпендикулярний до вектора
перпендикулярний до вектора 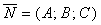 і їх скалярний добуток дорівнює нулю:
і їх скалярний добуток дорівнює нулю: 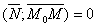 , або
, або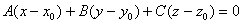 . (2.44)
. (2.44)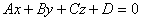 (2.45)
(2.45)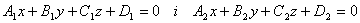 виписують з умов колінеарності й перпендикулярності їх нормальних векторів
виписують з умов колінеарності й перпендикулярності їх нормальних векторів 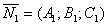 і
і 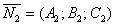 .
. Нехай дано яку-небудь пряму L, що проходить через точку
Нехай дано яку-небудь пряму L, що проходить через точку 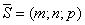 (називають напрямним вектором прямої). Позначимо через М(х,у,z) довільну точку прямої. З умов колінеарності векторів
(називають напрямним вектором прямої). Позначимо через М(х,у,z) довільну точку прямої. З умов колінеарності векторів 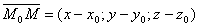 і
і 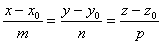 (2.46)
(2.46)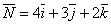 . (Відп.: 4х+3у+2z-27=0).
. (Відп.: 4х+3у+2z-27=0).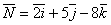 . (Відп.:
. (Відп.: 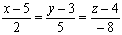 ).
).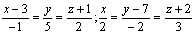 ).
).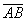 . (Відп.:
. (Відп.: 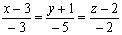 ).
).