Розглянемо три види ліній: еліпс, гіперболу і параболу, рівняння яких у прямокутній системі координат є рівняннями другого степеня. Такі лінії називають лініями другого порядку.
Познайомимося з найважливішими геометричними властивостями ліній другого порядку.
Розглянемо рівняння другого степеня з двома змінними у загальному вигляді
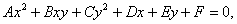 (2.32)
(2.32)
в якому А, В і С не дорівнюють одночасно нулю ( 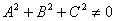 ).
).
Доводиться, що завжди можна вибрати систему координат таким чином, щоб коефіцієнт В дорівнював нулеві. А тому, не обмежуючи спільності, можна вважати, що у вихідному рівнянні (2.32) В =0.
Перепишемо тепер рівняння у такому вигляді
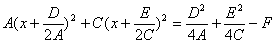
або
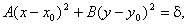
де
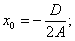
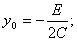
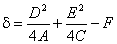 .
.
Для простоти дослідження вважатимемо 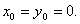 Тоді рівняння кривої прийме вигляд
Тоді рівняння кривої прийме вигляд
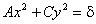 . (2.33)
. (2.33)
Насамперед розглянемо такі два випадки:
1) коефіцієнти А і С мають однакові знаки;
2) коефіцієнти А і С мають протилежні знаки.
Випадок 1. Криву другого порядку (2.33) називають кривою еліптичного типу, якщо коефіцієнти А і С мають однакові знаки. Для конкретності вважатимемо, що А>0, C>0 ( у протилежному випадку обидві частини рівняння можна домножити на (-1) ).
Можливі три випадки:
а) d>0; б) d=0; в) d<0.
Легко бачити, що у випадку d<0 крива (2.33) не має дійсних точок, а у випадку d=0 крива (2.33)вироджується в одну точку (0;0). Зупинимося на випадку d>0.
З (2.33) дістанемо рівняння
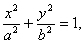 (2.34)
(2.34)
яке називають канонічним рівнянням еліпса з півосями 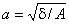 і
і 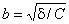 . У частинному випадку, коли а=b рівняння (2.34) є рівнянням кола
. У частинному випадку, коли а=b рівняння (2.34) є рівнянням кола 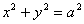 . Точки
. Точки 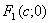 і
і 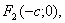 де
де
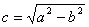 (2.35)
(2.35)
називають фокусами еліпса.
Відношення
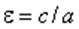 (2.36)
(2.36)
називають ексцентриситетом еліпса. Ексцентриситет характеризує форму еліпса. Очевидно, що 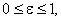 причому для кола
причому для кола 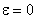 .
.
Точки 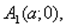
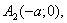
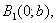
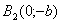 називають вершинами еліпса.
називають вершинами еліпса.
Обчислимо суму відстаней від будь-якої точки еліпса М(х;у) до його фокусів
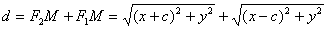 .
.
З урахуванням (2.34)-(2.36) дістанемо
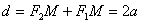 .
.
Отже, для будь-якої точки еліпса сума відстаней її до фокусів є величина стала і дорівнює 2а. Цю характеристичну властивість еліпса часто приймають за означення еліпса.
Приклад
Встановити вигляд і розміщення кривої
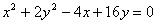
Розв’язання. Доповнимо доданки з х і у до повних квадратів, дістанемо
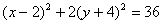
або
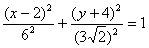
Покладемо 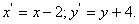 Маємо
Маємо
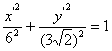 .
.
Отже, крива є еліпсом з центром 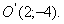
Випадок 2. Криву другого порядку (2.33) називають кривою гіперболічного типу, якщо коефіцієнти А і С мають протилежні знаки.
Для конкретності вважатимемо А>0, C<0.
Можливі три випадки:
а) d>0; б) d=0; в) d<0.
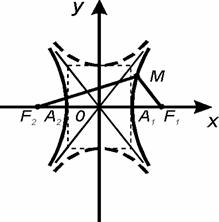
У першому випадку ( d>0 )з (2.33) дістанемо рівняння
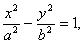 (2.37)
(2.37)
яке називають канонічним рівнянням гіперболи; тут 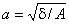 - дійсна піввісь,
- дійсна піввісь, 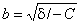 - уявна піввісь
- уявна піввісь
Фокуси гіперболи – точки 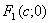 і
і 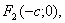 тут
тут 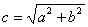 . Ексцентриситет гіперболи
. Ексцентриситет гіперболи 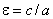 .
.
Вершини гіперболи – точки 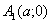 і
і 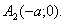
Можна довести, що для будь-якої точки гіперболи абсолютна величина різниці її відстаней до фокусів є величина стала і дорівнює 2а:
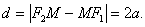
Цю характеристичну властивість гіперболи часто приймають за означення гіперболи.
Перепишемо рівняння гіперболи (2.37) у вигляді
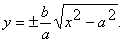 (2.38)
(2.38)
Для достатньо великих х можемо писати 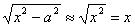 і рівняння (2.38) дістане вигляд
і рівняння (2.38) дістане вигляд
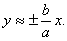
Такі прямі називають асимптотами гіперболи. Зокрема, для гіперболи 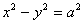 асимптоти
асимптоти 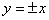 взаємно перпендикулярні і є бісектрисами координатних кутів.
взаємно перпендикулярні і є бісектрисами координатних кутів.
У другому випадку ( d=0 ) рівняння кривої має вигляд
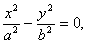
тобто дістаємо пару прямих
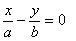 і
і 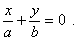
У третьому випадку ( d<0 ) дістанемо гіперболу
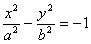
з півосями 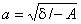 і
і 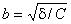 .
.
Цю гіперболу називають спряженою з гіперболою (2.37) (на малюнку вона зображена пунктиром).
Розглянемо обернену пропорційну залежність, що задається рівнянням
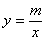 або
або 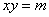 (2.39)
(2.39)
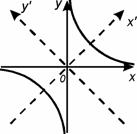
Графіком оберненої пропорційної залежності є рівностороння гіпербола з асимптотами – осями координат.
Якщо m>0, вітки гіперболи знаходяться в І і ІІІ квадрантах, якщо m<0 – в ІІ і IV квадрантах.
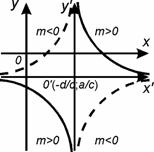
Розглянемо графік дробово-лінійної функції
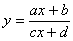 , (2.40)
, (2.40)
де 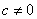 ,
, 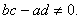
Перетворюючи (2.40), маємо
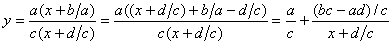 .
.
Перейдемо до нової системи координат 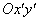 :
:
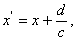
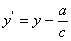 ;
;
поклавши 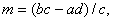 приведемо рівняння (2.40) до вигляду
приведемо рівняння (2.40) до вигляду
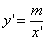 або
або 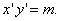
Отже, графіком дробово-лінійної функції (2.40) є рівностороння гіпербола з асимптотами
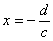 і
і 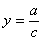 ,
,
паралельними осям координат.
Розглянемо тепер випадок рівняння кривої другого порядку (2.32), в якому В=0, а також один з коефіцієнтів А або С дорівнює нулю; для конкретності 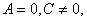 тобто
тобто
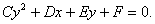 (2.41)
(2.41)
Нехай також 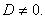 Доповнимо члени з у до повного квадрата
Доповнимо члени з у до повного квадрата
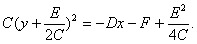
Покладемо
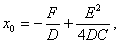
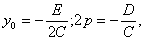
маємо
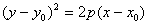 (2.42)
(2.42)
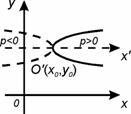
Криву (2.42) називають параболою, а точку 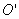 (х0;у0) – вершиною параболи, р – параметром параболи. Якщо p>0 вітки параболи направлені вправо, якщо p<0 – вліво. Пряма
(х0;у0) – вершиною параболи, р – параметром параболи. Якщо p>0 вітки параболи направлені вправо, якщо p<0 – вліво. Пряма 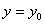 є віссю параболи.
є віссю параболи.
Якщо вершина параболи знаходиться в початку координат, то рівняння (2.42) має вигляд
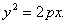 (2.43)
(2.43)
Якщо в рівнянні (2.43) поміняти місцями х та у, то одержимо 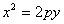 - рівняння параболи з вершиною в початку координат, симетричною відносно осі ординат.
- рівняння параболи з вершиною в початку координат, симетричною відносно осі ординат.
Розглянемо далі квадратний тричлен
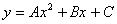
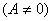
Звідси
Позначимо 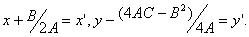
В новій системі координат 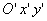 з центром
з центром 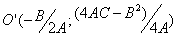 рівняння має вигляд
рівняння має вигляд 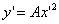 .
.
Отже, графіком квадратного тричлена
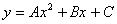
є парабола з вершиною в точці 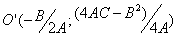 і віссю симетрії
і віссю симетрії 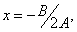 паралельною осі Оу.
паралельною осі Оу.


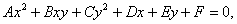 (2.32)
(2.32)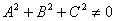 ).
).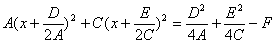
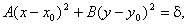
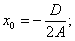
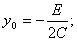
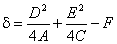 .
.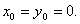 Тоді рівняння кривої прийме вигляд
Тоді рівняння кривої прийме вигляд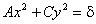 . (2.33)
. (2.33)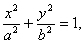 (2.34)
(2.34)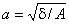 і
і 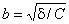 . У частинному випадку, коли а=b рівняння (2.34) є рівнянням кола
. У частинному випадку, коли а=b рівняння (2.34) є рівнянням кола 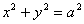 . Точки
. Точки 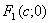 і
і 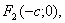 де
де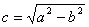 (2.35)
(2.35)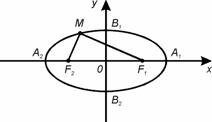
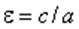 (2.36)
(2.36)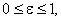 причому для кола
причому для кола 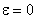 .
.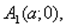
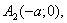
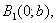
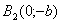 називають вершинами еліпса.
називають вершинами еліпса.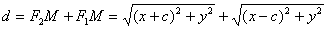 .
.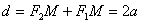 .
.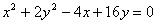
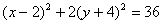
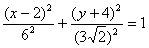
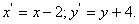 Маємо
Маємо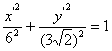 .
.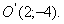
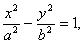 (2.37)
(2.37)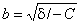 - уявна піввісь
- уявна піввісь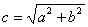 . Ексцентриситет гіперболи
. Ексцентриситет гіперболи 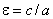 .
.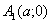 і
і 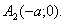
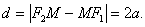
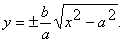 (2.38)
(2.38)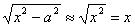 і рівняння (2.38) дістане вигляд
і рівняння (2.38) дістане вигляд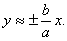
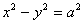 асимптоти
асимптоти 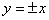 взаємно перпендикулярні і є бісектрисами координатних кутів.
взаємно перпендикулярні і є бісектрисами координатних кутів.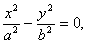
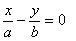 і
і 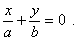
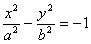
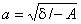 і
і 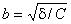 .
.
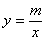 або
або 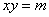 (2.39)
(2.39)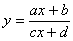 , (2.40)
, (2.40)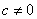 ,
, 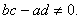
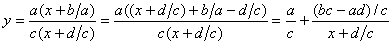 .
.
 :
: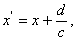
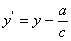 ;
;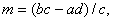 приведемо рівняння (2.40) до вигляду
приведемо рівняння (2.40) до вигляду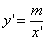 або
або 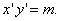
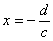 і
і 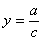 ,
,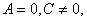 тобто
тобто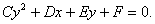 (2.41)
(2.41)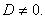 Доповнимо члени з у до повного квадрата
Доповнимо члени з у до повного квадрата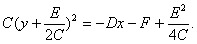
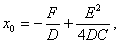
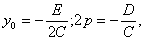
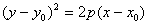 (2.42)
(2.42)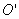 (х0;у0) – вершиною параболи, р – параметром параболи. Якщо p>0 вітки параболи направлені вправо, якщо p<0 – вліво. Пряма
(х0;у0) – вершиною параболи, р – параметром параболи. Якщо p>0 вітки параболи направлені вправо, якщо p<0 – вліво. Пряма 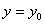 є віссю параболи.
є віссю параболи.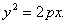 (2.43)
(2.43)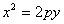 - рівняння параболи з вершиною в початку координат, симетричною відносно осі ординат.
- рівняння параболи з вершиною в початку координат, симетричною відносно осі ординат.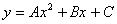
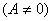
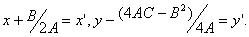
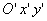 з центром
з центром 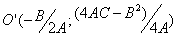 рівняння має вигляд
рівняння має вигляд 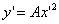 .
.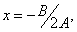 паралельною осі Оу.
паралельною осі Оу.