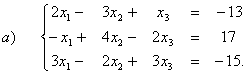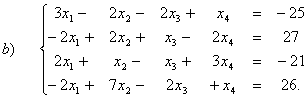Для будь-якого дійсного числа 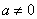 є число
є число 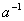 (його називають оберненим для
(його називають оберненим для 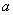 ) таке, що
) таке, що 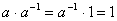 . Аналогічне поняття введемо також для квадратних матриць.
. Аналогічне поняття введемо також для квадратних матриць.
Квадратну матрицю 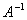 назвемо оберненою для квадратної матриці
назвемо оберненою для квадратної матриці 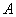 , якщо
, якщо
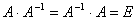 (1.17)
(1.17)
Не кожна квадратна матриця має обернену. Необхідну і достатню умови існування оберненої матриці дає теорема, яку ми подамо без доведення.
Теорема (про обернену матрицю ). Матриця 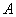 має обернену матрицю
має обернену матрицю 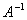 тоді і тільки тоді, коли
тоді і тільки тоді, коли 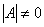 . Якщо ця умова виконана, то обернена матриця єдина і має таку будову: елементи її к – го стовпця
. Якщо ця умова виконана, то обернена матриця єдина і має таку будову: елементи її к – го стовпця 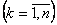 є алгебраїчні доповнення відповідних елементів к – го рядка матриці А, поділені на визначник
є алгебраїчні доповнення відповідних елементів к – го рядка матриці А, поділені на визначник 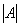 .
.
Якщо визначник матриці не є нулем ( 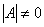 ), то таку матрицю називають невиродженою, у протилежному випадку (
), то таку матрицю називають невиродженою, у протилежному випадку ( 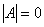 ) – виродженою.
) – виродженою.
Послідовність обернення матриці може бути такою .
1. Обчислюємо визначник матриці. Якщо 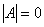 , то матриця
, то матриця 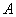 вироджена і оберненої матриці
вироджена і оберненої матриці 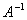 немає. Якщо
немає. Якщо 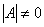 , то матриця
, то матриця 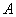 невироджена і є обернена матриця.
невироджена і є обернена матриця.
2. Обчислюємо алгебраїчні доповнення 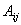 кожного елемента
кожного елемента 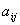
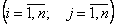 матриці
матриці 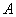 .
.
3. Записуємо союзну матрицю 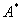 – це матриця, елементами якої є алгебраїчні доповнення
– це матриця, елементами якої є алгебраїчні доповнення 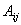 елементів матриці
елементів матриці 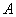 , причому алгебраїчні доповнення елементів рядка записані у відповідних стовпцях:
, причому алгебраїчні доповнення елементів рядка записані у відповідних стовпцях:
 .
.
4. Складаємо обернену матрицю за формулою
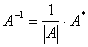 . (1.18)
. (1.18)
Приклад. Обчислити матрицю обернену для матриці
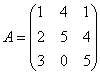 .
.
Розв’язання. 1. Обчислюємо визначник матриці 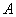 :
:
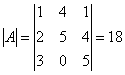 .
. 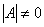 .
.
2. Обчислюємо алгебраїчні доповнення елементів матриці 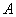 :
:
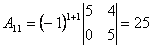 ;
; 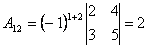 ;
;
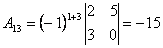 ;
; 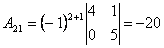 ;
;
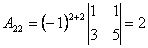 ;
; 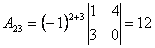 ;
;
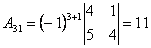 ;
; 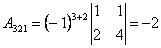 ;
;
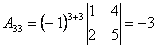 .
.
3. Записуємо союзну матрицю
 .
.
4. Обчислюємо обернену матрицю
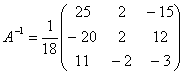 .
.
Розглянемо тут і друге правило побудови оберненої матриці задопомогоюелементарних перетворень Жордана-Гаусса рядків матриці.
Елементарними назвемо такі перетворення рядків довільної матриці:
- перестанеовка двох якихось рядків матриці;
- множення елементів довільного рядка матриці на відмінне від нуля число;
- додавання до елементів будь-якого рядка матриці відповідних елементів іншого рядка, помножених на число;
- викреслювання нульового рядка матриці.
Доводиться, що кожну невироджену матрицю А задопомогою елементарних можна привести до одиничної матриці Е.
За цим правилом послідовність подудови оберненої матриці може бути такою:
1) справа від даної матриці 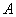 з ненульовим визначником дописують через відокремлюючу риску одиничну матрицю
з ненульовим визначником дописують через відокремлюючу риску одиничну матрицю 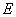 того самого порядку:
того самого порядку: 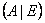 ;
;
2) елементарними перетвореннями рядків матрицю зліва риски перетворюють в одиничну, виконуючи одночасно аналогічні перетворення рядків матриці справа риски;
3) матриця справа риски, яку так діставнемо, і є оберненою для матриці А: 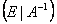 .
.
Подамо правило обчислення елементів перетвореної матриці:
1. Діагональні елементи перетворюваної матриці, починаючи з 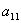 , вважаємо ведучими; при цьому рядки і стовпці , які містять ведучий елемент, назвемо ведучими.
, вважаємо ведучими; при цьому рядки і стовпці , які містять ведучий елемент, назвемо ведучими.
2. Елементи ведучого рядка одержуємо з відповідних елементів рядка попередньої матриці діленням на ведучий елемент.
3. Всі елементи ведучого стовпця, крім ведучого елемента, дорівнюють нулю (ведучий елемент дорівнює 1).
4. Всі решту елементів одержуємо за правилом прямокутника:
в матриці виділяємо прямокутник так, що елемент, який перераховуємо і ведучий елемент утворюють одну з його діагоналей; далі з добутку цих елементів віднімаємо добуток елементів, які утворюють другу діагональ, і одержану так різницю ділимо на ведучий елемент
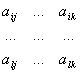 ;
; 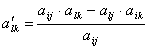 .
.
Приклад. Обчислити матрицю обернену для матриці
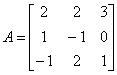 .
.
Розв’язання.
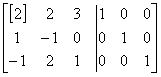
 Þ
Þ 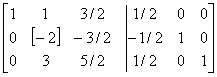 Þ
Þ
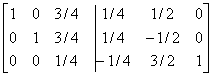 Þ
Þ 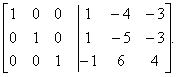
Отже,
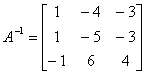 .
.
Звернемось тепер до системи лінійних рівнянь
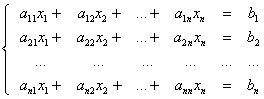
Особливо важливо, що дану систему можна записати у вигляді одного-єдиного матричного рівняння. Для цього введемо в розгляд матриці:
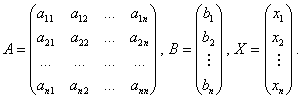
Добутком матриць 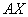 є матриця типу
є матриця типу 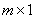 ( m рядків і один стовпець ), тобто стовпець з m чисел. Випишемо ці числа:
( m рядків і один стовпець ), тобто стовпець з m чисел. Випишемо ці числа:
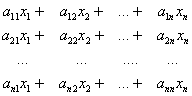

Тепер очевидно, що систему можна записати у вигляді такого матричного рівняння
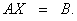
Таке рівняння є матричною формою системи рівнянь.
Якщо її визначник 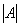
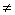 0 , то існує обернена матриця
0 , то існує обернена матриця 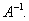 Домножимо обидві частини останього рівняння зліва на
Домножимо обидві частини останього рівняння зліва на 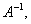 одержимо
одержимо
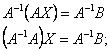
враховуючи, що 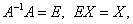 маємо
маємо
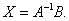
Такий матричний запис розв’язку системи n лінійних рівнянь з n невідомими, за умови, що матриця 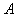 системи не вироджена.
системи не вироджена.
Приклад. Розв’язати систему рівнянь
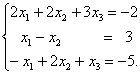
Розв’язання .Обчислимо визначник матриці системи
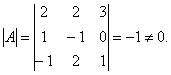

Матриця  системи не вироджена. Знаходимо обернену матрицю
системи не вироджена. Знаходимо обернену матрицю  .
.
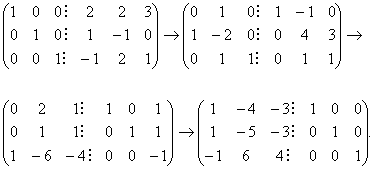
Отже
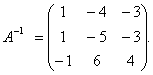
Розв’язок системи
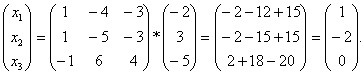
Відповідь: {(1;-2;0)}.
Вправи.
1. Обчислити матриці обернені для даних матриць:
а) 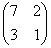 ; b)
; b) 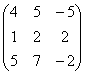 ; c)
; c) 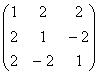 ;
;
Відповідь.
a) 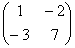 ; b)
; b) 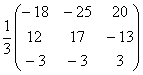 ; c)
; c) 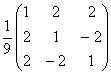 .
.
2. Розв’язати системи лінійних рівнянь за допомогою оберненої матриці:
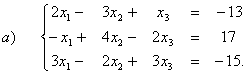
Відповідь: {(-1;3;-2)}.
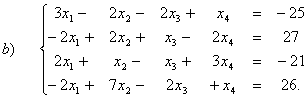


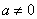 є число
є число 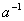 (його називають оберненим для
(його називають оберненим для 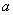 ) таке, що
) таке, що 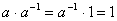 . Аналогічне поняття введемо також для квадратних матриць.
. Аналогічне поняття введемо також для квадратних матриць.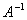 назвемо оберненою для квадратної матриці
назвемо оберненою для квадратної матриці 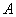 , якщо
, якщо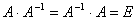 (1.17)
(1.17)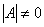 . Якщо ця умова виконана, то обернена матриця єдина і має таку будову: елементи її к – го стовпця
. Якщо ця умова виконана, то обернена матриця єдина і має таку будову: елементи її к – го стовпця 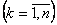 є алгебраїчні доповнення відповідних елементів к – го рядка матриці А, поділені на визначник
є алгебраїчні доповнення відповідних елементів к – го рядка матриці А, поділені на визначник 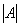 .
.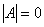 ) – виродженою.
) – виродженою.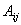 кожного елемента
кожного елемента 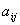
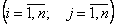 матриці
матриці 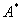 – це матриця, елементами якої є алгебраїчні доповнення
– це матриця, елементами якої є алгебраїчні доповнення  .
.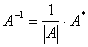 . (1.18)
. (1.18)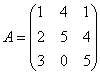 .
.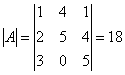 .
. 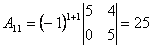 ;
; 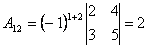 ;
;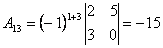 ;
; 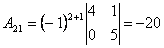 ;
;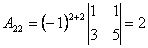 ;
; 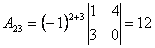 ;
;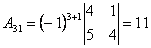 ;
; 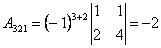 ;
;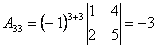 .
. .
.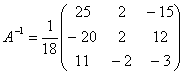 .
. того самого порядку:
того самого порядку:  ;
;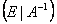 .
.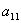 , вважаємо ведучими; при цьому рядки і стовпці , які містять ведучий елемент, назвемо ведучими.
, вважаємо ведучими; при цьому рядки і стовпці , які містять ведучий елемент, назвемо ведучими.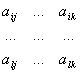 ;
; 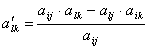 .
.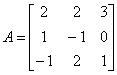 .
.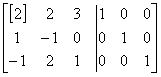
 Þ
Þ 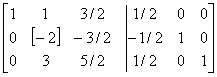 Þ
Þ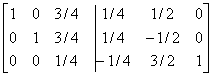 Þ
Þ 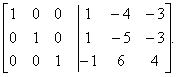
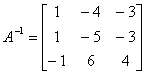 .
.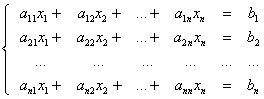
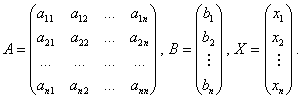
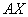 є матриця типу
є матриця типу 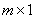 ( m рядків і один стовпець ), тобто стовпець з m чисел. Випишемо ці числа:
( m рядків і один стовпець ), тобто стовпець з m чисел. Випишемо ці числа: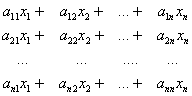
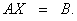
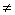 0 , то існує обернена матриця
0 , то існує обернена матриця 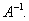 Домножимо обидві частини останього рівняння зліва на
Домножимо обидві частини останього рівняння зліва на 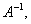 одержимо
одержимо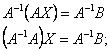
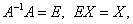 маємо
маємо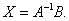
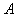 системи не вироджена.
системи не вироджена.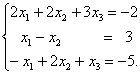
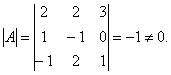
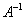 .
.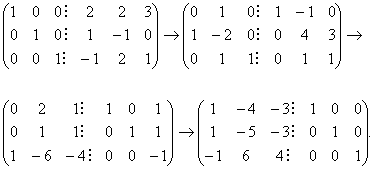
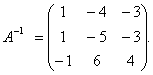
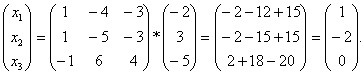
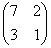 ; b)
; b) 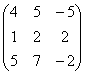 ; c)
; c) 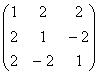 ;
;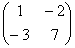 ; b)
; b) 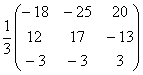 ; c)
; c) 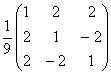 .
.