Викладач: Гуменчук М.П.
Вінниця 2013
університет університет  Рецензент: Черешнюк О.М.
Рецензент: Черешнюк О.М.
Розглянуто і схвалено
на засіданні ц/к природничих та фундаментальних дисциплін
Протокол № ______ від «_____» _________2013 р.
Голова ц/к __________( Гаращук С.К.)
Укладач:Гуменчук М.П. викладач-спеціаліст вищої категорії
Рецензент: Черешнюк О.М. викладач-спеціаліст вищої категорії
Розглянуто і ухвалено на засіданні ц/к вищої математики та інформатики
Протокол №______ від «____»_____________2013 р.
Голова ц/к ______________М.П. Гуменчук
Розділ1. Елементи лінійної алгебри
Тема 1.1. Розклад визначників за елементами рядка або стовпця
Поняття визначника матриці будь-якого порядку ми введемо індукцією за порядком матриці. Це дозволяє, знаючи правило обчислення визначника матриці порядку ( 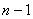 ), одержати правило обчислення визначника матриці порядку
), одержати правило обчислення визначника матриці порядку 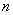 . Для цього введемо поняття мінора і алгебраїчного доповнення будь-якого елемента матриці.
. Для цього введемо поняття мінора і алгебраїчного доповнення будь-якого елемента матриці.
Нехай 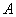 – довільна квадратна матриця порядку
– довільна квадратна матриця порядку 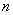 .
.
Означення 1Мінором 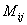 елемента
елемента 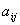 матриці
матриці 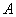 порядку
порядку 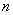 називається визначник матриці порядку
називається визначник матриці порядку 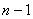 , одержаної з матриці
, одержаної з матриці 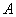 вилученням її
вилученням її 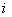 -го рядка і
-го рядка і 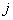 -го стовпця.
-го стовпця.
Наприклад , мінором 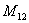 елемента
елемента 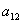 матриці порядку 3 буде :
матриці порядку 3 буде :
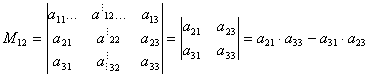 .
.
Зауважимо , що матриця прядку 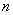 має
має 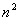 мінорів порядку (
мінорів порядку ( 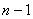 ).
).
Означення 2. Алгебраїчним доповненням 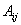 елемента
елемента 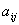 матриці
матриці 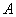 порядку
порядку 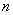 називається її мінор , взятий із знаком
називається її мінор , взятий із знаком 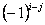
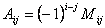
Приклад . Обчислити алгебраїчні доповнення всіх елементів матриці
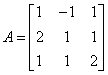 .
.
Розв’язання .
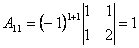 ;
; 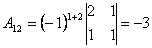 ;
;
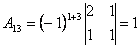 ;
;
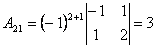 ;
; 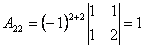 ;
;
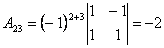 ;
;
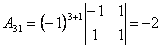 ;
; 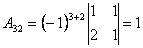 ;
;
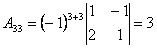 .
.
Має місце наступна основна теорема , яку подаємо без доведення .
Теорема. Визначник квадратної матриці дорівнює сумі добутків елементів будь-якого рядка чи стовпця на їх алгебраїчне доповнення
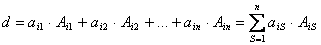 (1.15)
(1.15)
(розклад за елементами 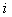 -го рядка;
-го рядка; 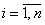 );
);
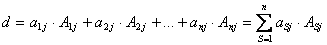 (1.16)
(1.16)
(розклад за елементами 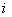 -го стовпця;
-го стовпця; 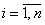 );
);


 Рецензент: Черешнюк О.М.
Рецензент: Черешнюк О.М.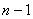 ), одержати правило обчислення визначника матриці порядку
), одержати правило обчислення визначника матриці порядку 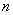 . Для цього введемо поняття мінора і алгебраїчного доповнення будь-якого елемента матриці.
. Для цього введемо поняття мінора і алгебраїчного доповнення будь-якого елемента матриці.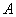 – довільна квадратна матриця порядку
– довільна квадратна матриця порядку 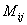 елемента
елемента 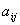 матриці
матриці 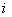 -го рядка і
-го рядка і 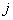 -го стовпця.
-го стовпця.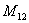 елемента
елемента 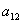 матриці порядку 3 буде :
матриці порядку 3 буде :
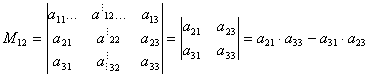 .
.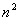 мінорів порядку (
мінорів порядку ( 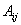 елемента
елемента 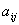 матриці
матриці 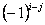
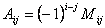
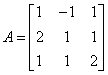 .
.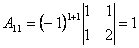 ;
; 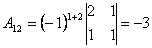 ;
;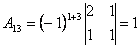 ;
;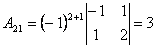 ;
; 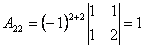 ;
;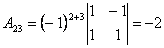 ;
;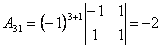 ;
; 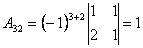 ;
;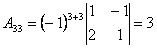 .
.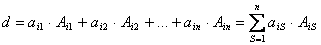 (1.15)
(1.15) 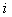 -го рядка;
-го рядка; 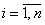 );
);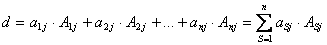 (1.16)
(1.16)