Множиною називатимемо будь-яку сукупність об’єктів (елементів множини). Множини можуть містити скінченну або нескінченну кількість елементів. До нескінченних відносяться: множина натуральних чисел N={1, 2, 3,…},
множина цілих чисел Z={0, ±1, ±2, ±3,…},
множина раціональних чисел 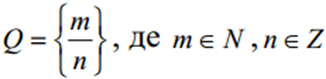 ,
,
які можна надати у виді десяткового скінченного дробу або нескінченного періодичного дробу,множина дійсних чисел, яка включає в себе раціональні числа, а також
ірраціональні числа, які надаються нескінченним неперіодичним дробом.
Множину всіх точок х, які задовольняють нерівності
1)а£х£b називають відрізком та позначають x є [a; b],
2) а£х£b або а£х<b називають півінтервалом та позначають x є (a; b] або x є [a; b),
3)а<х<b називають інтервалом та позначають x є (a; b).
Відрізки, півінтервали та інтервали називають проміжками. Розглядатимемо також нескінченні проміжки, використовуючи символи -¥, +¥, так множину дісних чисел позначають (-¥, +¥).
Околом точки а називається будь-який інтервал (a; b), що містить точку а. Інтервал (a-e; a+e), де а - будь-яке число, e - додатне число, називається e околом точки а. 
Це інтервал, симетричний відносно точки а, точка а називається центром інтервалу, а число e радіусом епсілон-окола.
Модуль (абсолютна величина).
Абсолютною величиною (або модулем) дійсного числа х (позначається |x|) називається невід’ємне дійсне число, яке задовольняє умовам: |х|=х, якщо х³0; |х|= - х, якщо х£0.
З означення випливає , що для будь-якого х правильною є нерівність х£|х|.
1)Абсолютна величина алгебраїчної суми декількох дійсних чисел не більше суми абсолютних величин доданків:
|х+у|£|х|+|у|
2)Абсолютна величина різниці не менше різниці абсолютних величин зменшуваного та від’ємника:
|х-у|³|х|-|у|, |х|>|у|
3)Абсолютна величина добутку дорівнює добутку абсолютних величин множників:
|х×у|³|х|×|у|
4) Абсолютна величина частки дорівнює частці абсолютних величин:
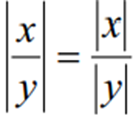


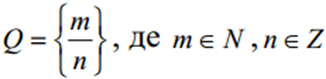 ,
,