Пряма лінія як перетин двох площин.

Пряму у просторі можна задати як лінію перетину двох площин у прямокутній системі координат:

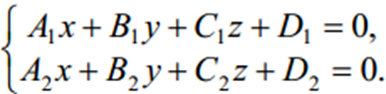
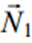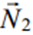Зрозуміло, що ці площини мають бути непаралельними, тобто їхні нормальні вектори , — не колінеарні. Система називається загальним рівнянням прямої.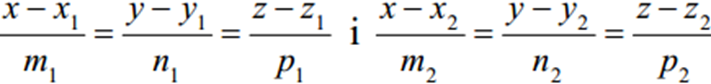

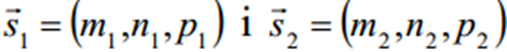40.Кут між двома прямими у просторі. Умова || та ^ двох прямих у просторі.

Для знаходження кута між двома прямими

візьмемо до уваги, що вектори

колінеарні відповідним прямим і скористаємося формулою: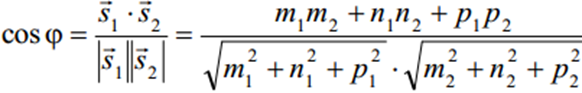

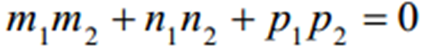
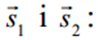
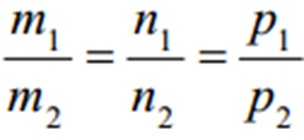
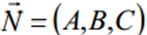З останньої формули випливає умова перпендикулярності двох прямих:

а умову паралельності двох прямих дістанемо як умову колінеарності напрямних векторів

41.Кут між прямою та площиною. Умови || та ^ прямої та площини.

Знайдемо кут між площиною і прямою

Кут j між площиною і прямою дорівнює куту між прямою і її проекцією на площину. Вектор — перпендикулярний до площини, а кут a, який він утворює з вектором 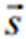, разом з j у сумі дорівнює 90°. Тобто a+j=90°. Знайдемо кут a як кут між двома векторами.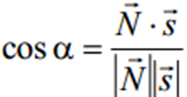

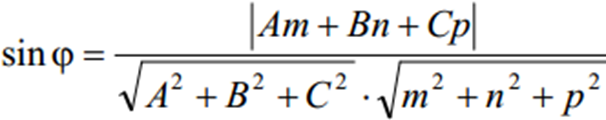
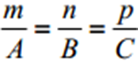Якщо a<90°, то cosa=cos(90-j)=sinj, а якщо a>90°, то cosa=cos(90-j)= - sinj, у будь-якому разі sinj=|cosa|. Отже,

Якщо , то пряма перпендикулярна до площини, а коли Am+Bn+Cp=0, пряма паралельна площині.