Розклад вектора в координатному базисі i, j, k. Лінійні операції над векторами в системі координат.

Нехай

Тоді

Тобто, лінійні операції над векторами виконуються покомпонентно: при додаванні (відніманні) векторів їх відповідні кординати додаються (віднімаються); при множенні вектора на число кожна координата множиться на це число.

28.1.Означення скалярного добутку векторів. Скалярний добуток двох векторів заданих координатами. Основні властивості скалярного добутку векторів. Кут між двома векторами заданими їх координатами. Умові || та ^ двох векторів.

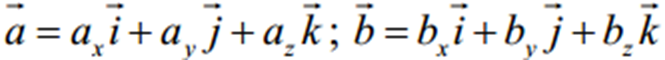
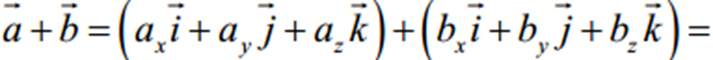
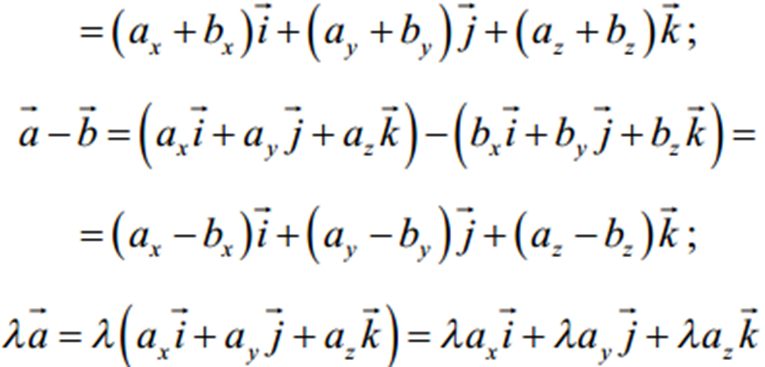
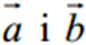Скалярним добутком двох векторів називається число, яке дорівнює добутку модулів цих векторів на косинус кута між ними.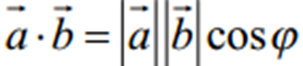

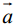Якщо вектори задані їх координатами =(а_х ; а_у ; а_z) ; 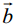=(b_x ; b_y ; b_z), то скалярний добуток можна знайти як суму добутків відповідних координат:

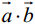=a_xb_x+a_yb_y+a_zb_z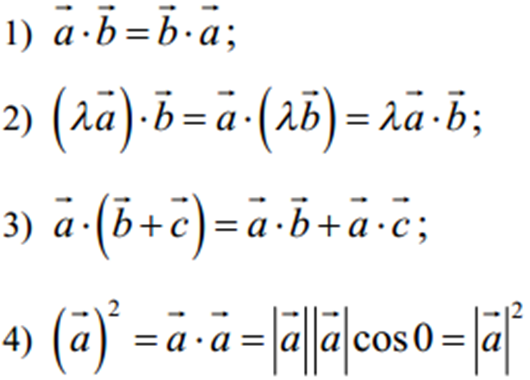

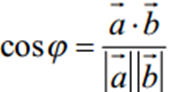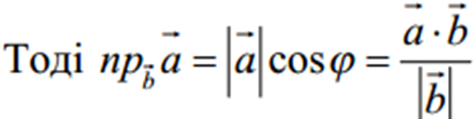
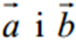Властивості скалярного добутку:

Безпосередньо з означення маємо .

Умова колінеарності (паралельності) двох векторів: Два ненульові вектори колінеарні тоді і тільки тоді, коли їх відповідні координати пропорційні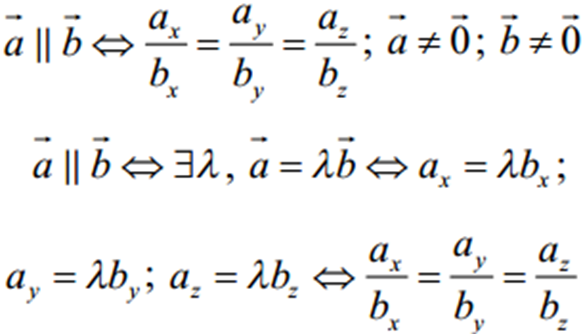

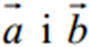Умова перпендикулярності (ортогональності) двох векторів: два ненульові вектори взаємно перпендикулярні тоді і тільки тоді , коли їх скалярний добуток дорівнює нулю