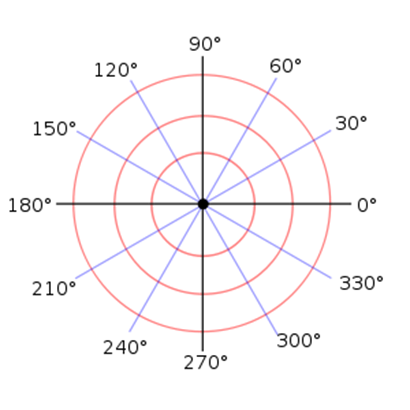
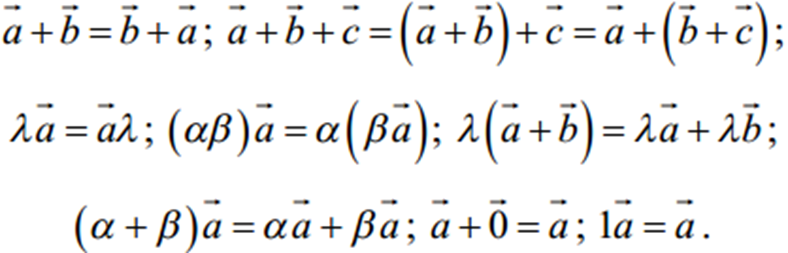 Полярна система координат — двовимірна система координат, в якій кожна точка на площині визначається двома числами — кутом та відстанню. Полярна система координат особливо корисна у випадках, коли відношення між точками найпростіше зобразити у вигляді відстаней та кутів; в поширенішій, Декартовій, або прямокутній системі координат, такі відношення можна встановити лише шляхом застосування тригонометричних рівнянь.
Полярна система координат — двовимірна система координат, в якій кожна точка на площині визначається двома числами — кутом та відстанню. Полярна система координат особливо корисна у випадках, коли відношення між точками найпростіше зобразити у вигляді відстаней та кутів; в поширенішій, Декартовій, або прямокутній системі координат, такі відношення можна встановити лише шляхом застосування тригонометричних рівнянь.
Пару полярних координат r та φ можна перевести в Декартові координати x та y шляхом застосування тригонометричних функцій синуса та косинуса: x=r cosj y=r sinj
в той час як дві Декартові координати x та y можуть бути переведені в полярну координату r: r2=y2+x2 (за теоремою Піфагора).
Для визначення кутової координати φ, слід взяти до уваги два такі міркування:
· Для  = 0, φ може бути довільним дійсним числом.
= 0, φ може бути довільним дійсним числом.
· Для  ≠ 0, аби отримати унікальне значення φ, слід обмежитись інтервалом в 2π. Зазвичай, обирають інтервал [0, 2π) або (−π, π].
≠ 0, аби отримати унікальне значення φ, слід обмежитись інтервалом в 2π. Зазвичай, обирають інтервал [0, 2π) або (−π, π].
Для обчислення φ в інтервалі [0, 2π), можна скористатись такими рівняннями (arctg позначає обернену функцію до тангенсу):
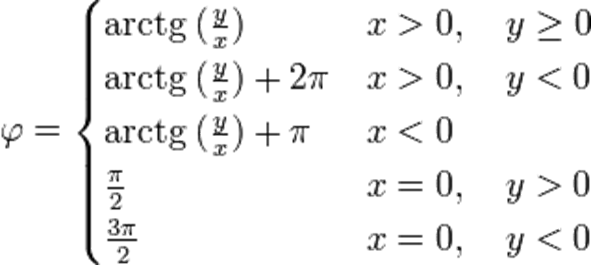
Для обчислення φ в інтервалі (−π, π], можна скористатись такими рівняннями:
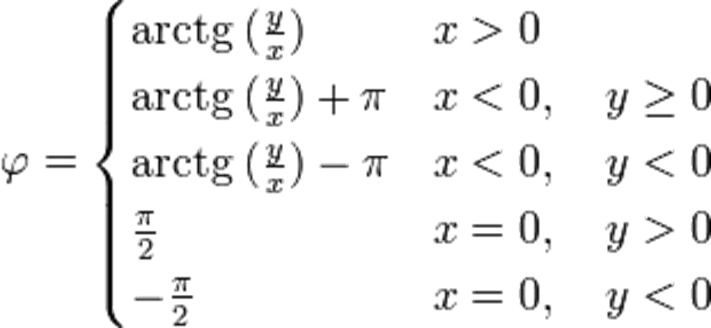
Означення вектора, модуль вектора. Колінеарність та компланарність векторів. Лінійні дії з векторами.
Величина, яка характеризується не тільки числовим значенням, а й напрямком, називається векторною величиною (вектором). Приклади векторів: швидкість, сила, момент сили, напруженість електричного поля і т. п. Вектор зображується напрямленим прямолінійним відрізком, в якому вказано його початок A і кінець B .
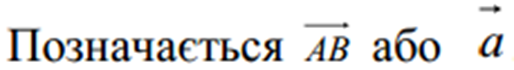
Модулем (абсолютною величиною, довжиною) вектора називається довжина відрізка, який зображає цей вектор.
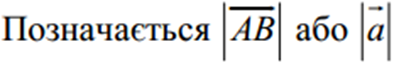
Вектори, які лежать на паралельних прямих або на одній прямій, називаються колінеарними (паралельними). Позначається 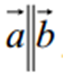 .
.
Вектори, які лежать у паралельних площинах або в одній площині, називаються компланарними.
Сумою 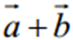 двох векторів
двох векторів 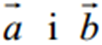 називається вектор, який визначається за правилом трикутника або за правилом паралелограма.
називається вектор, який визначається за правилом трикутника або за правилом паралелограма.
Добутком вектора 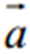 на число l називається вектор
на число l називається вектор 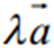 , який задовольняє наступним умовам:
, який задовольняє наступним умовам: 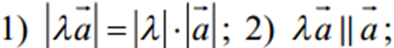 3) якщо l>0, то вектори
3) якщо l>0, то вектори 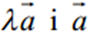 напрямлені в один бік; якщо l<0 , то вектори
напрямлені в один бік; якщо l<0 , то вектори 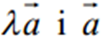 напрямлені в протилежні боки; якщо l=0, то
напрямлені в протилежні боки; якщо l=0, то 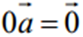 .
.
Вектор 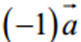 називається протилежним вектору
називається протилежним вектору 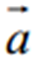 і позначається
і позначається 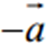 .
.
Різницею 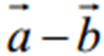 двох векторів
двох векторів 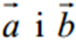 називається вектор, який в сумі з вектором
називається вектор, який в сумі з вектором 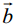 дає вектор
дає вектор 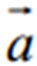 . Різниця
. Різниця 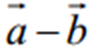 обчислюється за формулою
обчислюється за формулою 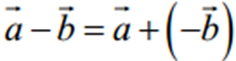 .
.
Розглянуті операції називаються лінійними, оскільки мають відповідні властивості:
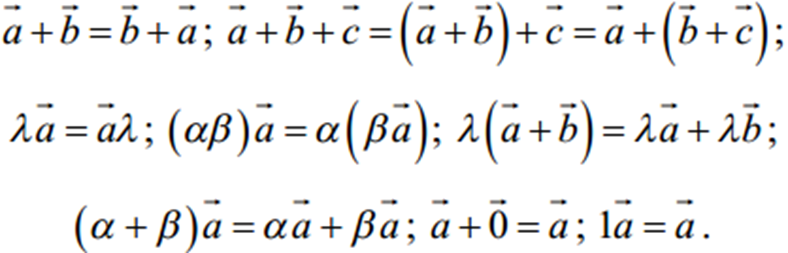


 Полярна система координат — двовимірна система координат, в якій кожна точка на площині визначається двома числами — кутом та відстанню. Полярна система координат особливо корисна у випадках, коли відношення між точками найпростіше зобразити у вигляді відстаней та кутів; в поширенішій, Декартовій, або прямокутній системі координат, такі відношення можна встановити лише шляхом застосування тригонометричних рівнянь.
Полярна система координат — двовимірна система координат, в якій кожна точка на площині визначається двома числами — кутом та відстанню. Полярна система координат особливо корисна у випадках, коли відношення між точками найпростіше зобразити у вигляді відстаней та кутів; в поширенішій, Декартовій, або прямокутній системі координат, такі відношення можна встановити лише шляхом застосування тригонометричних рівнянь. = 0, φ може бути довільним дійсним числом.
= 0, φ може бути довільним дійсним числом.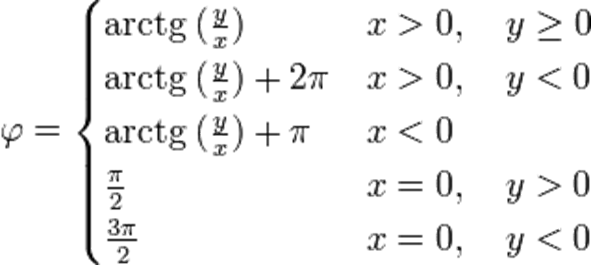
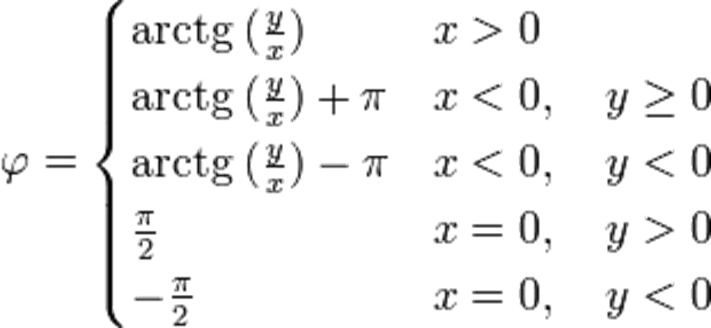
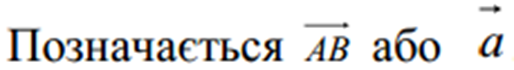
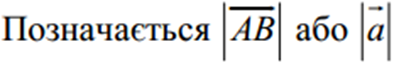
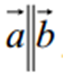 .
.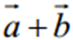 двох векторів
двох векторів 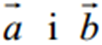 називається вектор, який визначається за правилом трикутника або за правилом паралелограма.
називається вектор, який визначається за правилом трикутника або за правилом паралелограма.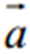 на число l називається вектор
на число l називається вектор 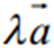 , який задовольняє наступним умовам:
, який задовольняє наступним умовам: 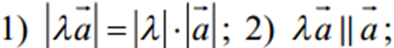 3) якщо l>0, то вектори
3) якщо l>0, то вектори 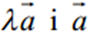 напрямлені в один бік; якщо l<0 , то вектори
напрямлені в один бік; якщо l<0 , то вектори 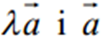 напрямлені в протилежні боки; якщо l=0, то
напрямлені в протилежні боки; якщо l=0, то 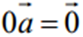 .
.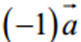 називається протилежним вектору
називається протилежним вектору 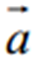 і позначається
і позначається 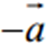 .
.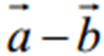 двох векторів
двох векторів 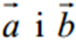 називається вектор, який в сумі з вектором
називається вектор, який в сумі з вектором 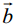 дає вектор
дає вектор 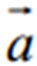 . Різниця
. Різниця 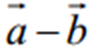 обчислюється за формулою
обчислюється за формулою 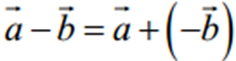 .
.