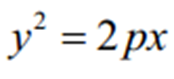Параболою називається множина всіх точок площини, для кожної з яких відстань від заданої точки площини F (фокусапараболи) дорівнює відстані до заданої прямої d l (директриси параболи), що не проходить через фокус.
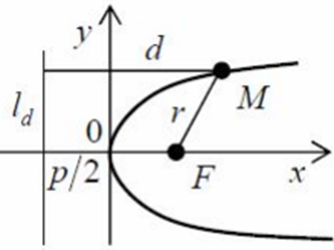
Для довільної точки M(x; y) параболи r=d, де r = MF – фокальний радіус точки M(x; y); d – відстань точки M(х ; у) до директриси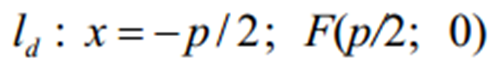 
- фокус; p – параметр параболи (відстань від фокуса до директриси), p > 0 . Тоді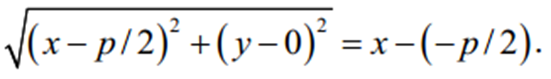 
Підносячи до квадрата і спрощуючи, одержимо канонічне рівняння параболи
