Нехай графік неперервної та неперервно диференційовної функції 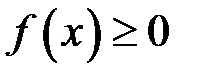 обертається навколо відрізка
обертається навколо відрізка 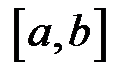 осі
осі 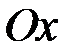 . Тоді площа поверхні утвореного таким чином тіла знаходиться за формулою:
. Тоді площа поверхні утвореного таким чином тіла знаходиться за формулою:
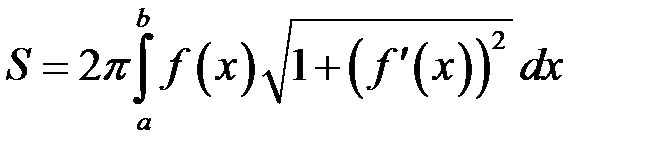 . (17.1)
. (17.1)
Якщо криву задано в параметричній формі 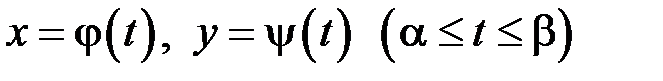 , де
, де 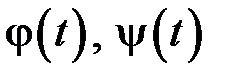 – неперервно диференційовні на відрізку
– неперервно диференційовні на відрізку 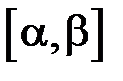 функції, причому
функції, причому 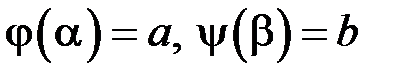 , то
, то
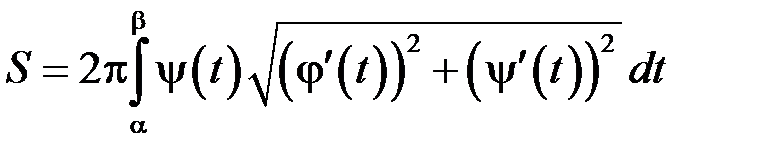 . (17.2)
. (17.2)
Якщо криву задано рівнянням у полярній системі координат 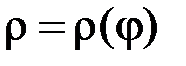 ,
, 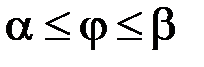 , то площа поверхні тіла, яке утворено обертанням фігури, обмеженої графіком функції
, то площа поверхні тіла, яке утворено обертанням фігури, обмеженої графіком функції 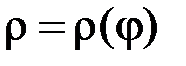 та променями
та променями 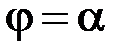 ,
, 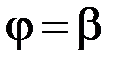 навколо полярної осі, дорівнює:
навколо полярної осі, дорівнює:
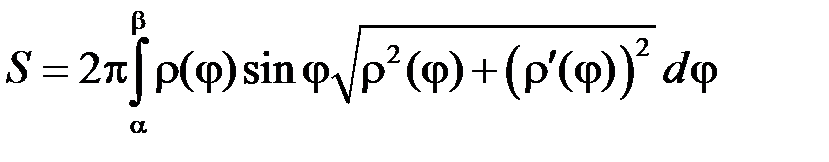 . (17.3)
. (17.3)
Приклади.
1. Знайти площу поверхні параболоїда, утвореного обертанням навколо осі 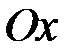 дуги параболи
дуги параболи 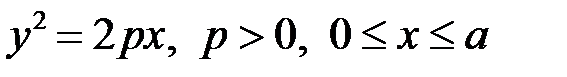 (рис. 21).
(рис. 21).
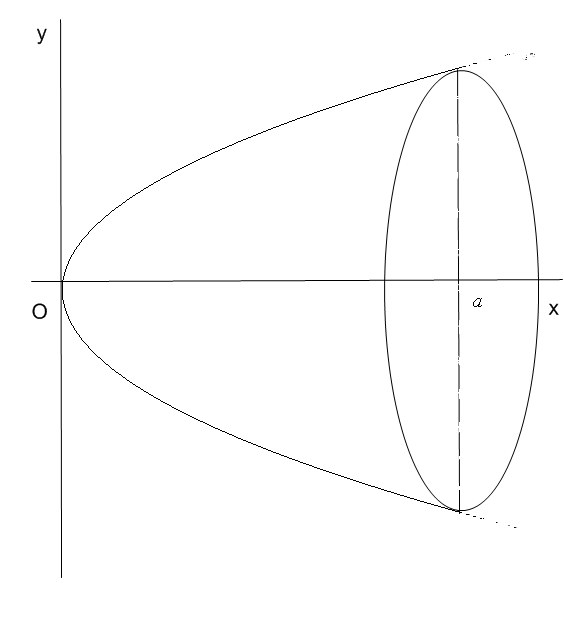
Рис. 21.
Маємо:
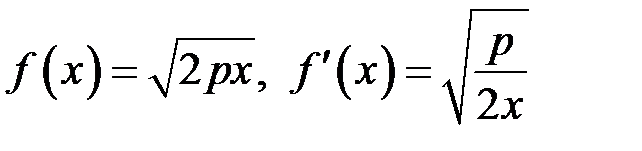 ,
,
і згідно з формулою (17.1):
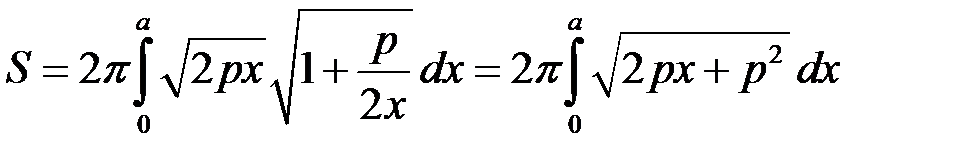
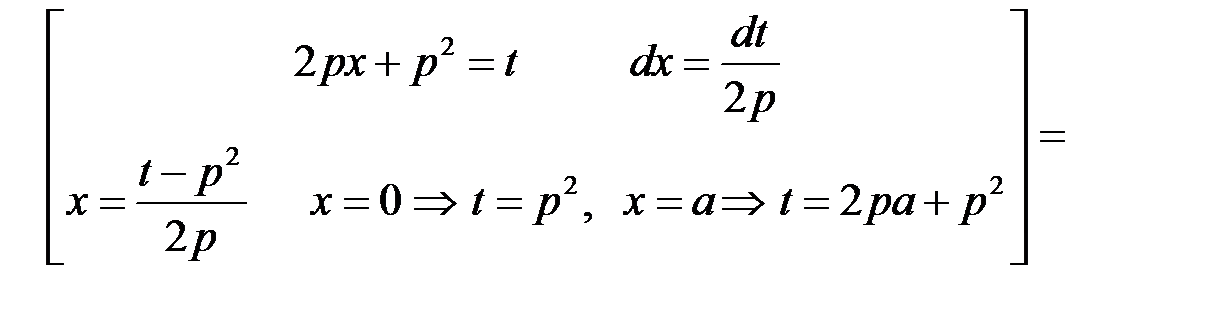
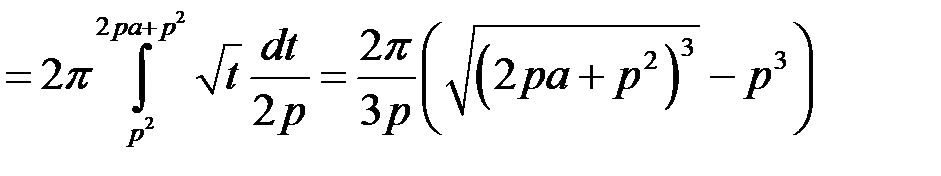 .
.
2. Знайти площу поверхні еліпса з півосями 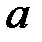 і
і 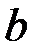 (
( 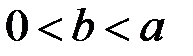 ).
).
Запишемо рівняння еліпса в параметричній формі: 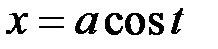 ,
, 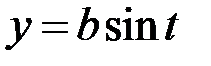 . Введемо до розгляду ексцентриситет еліпса:
. Введемо до розгляду ексцентриситет еліпса: 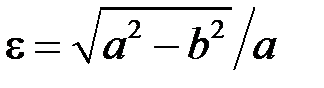 . Шукану площу можна отримати як подвоєну площу поверхні тіла, утвореного обертанням чверті еліпса, розташованої у 1-му квадранті, навколо осі
. Шукану площу можна отримати як подвоєну площу поверхні тіла, утвореного обертанням чверті еліпса, розташованої у 1-му квадранті, навколо осі 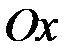 . Отже згідно з формулою (17.2) маємо:
. Отже згідно з формулою (17.2) маємо:
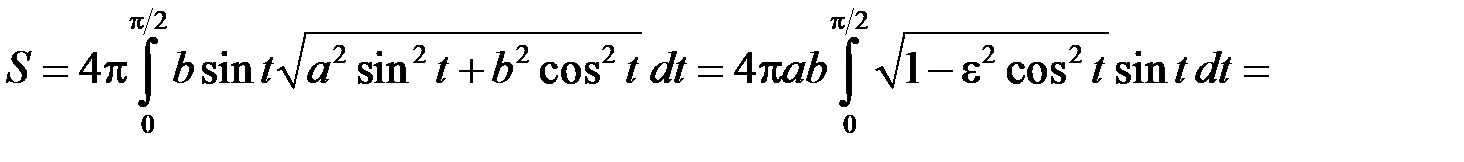
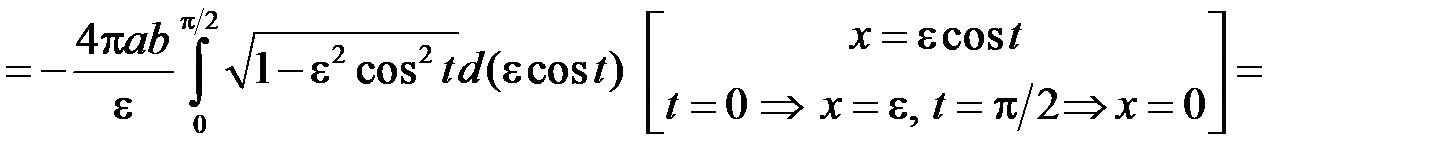
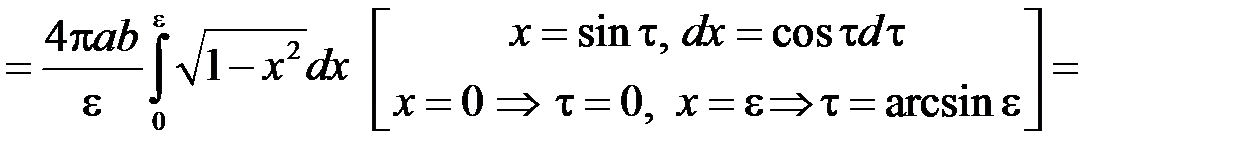
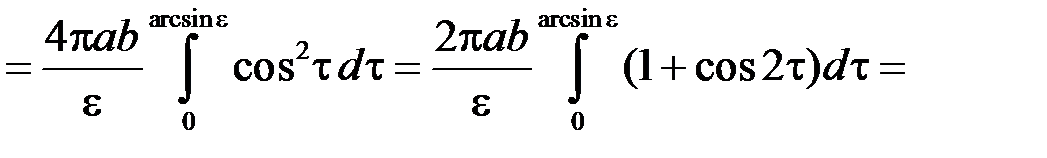
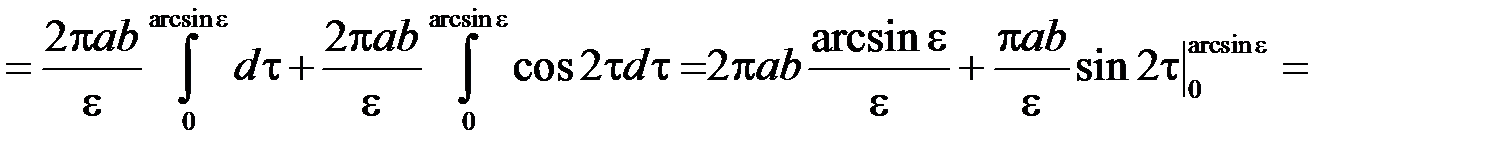
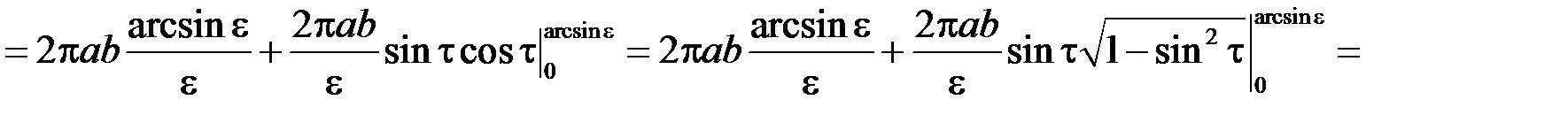
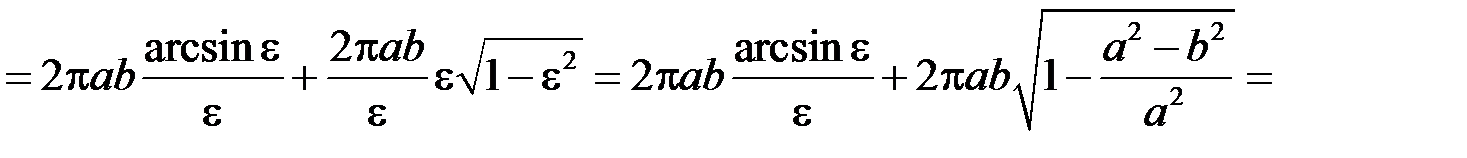
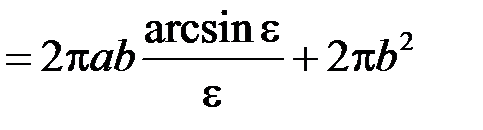 .
.
Зокрема, з цієї формули при 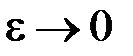 (
( 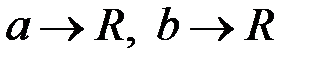 ) отримується формула площі поверхні сфери радіуса
) отримується формула площі поверхні сфери радіуса  :
: 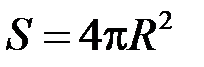 .
.
3. Знайти площу поверхні тіла, утвореного обертанням лемніскати Бернуллі 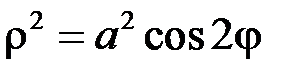 навколо полярної осі.
навколо полярної осі.
Шукану площу знайдемо як подвоєну площу поверхні тіла, утвореного обертанням чверті лемніскати, розташованої у 1-му квадранті, тобто 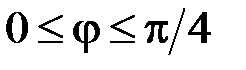 . Згідно з формулою (17.3) маємо:
. Згідно з формулою (17.3) маємо:
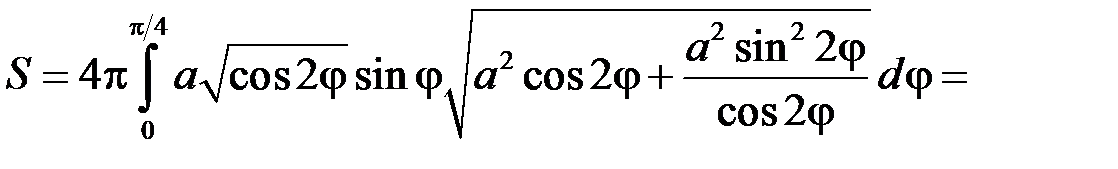
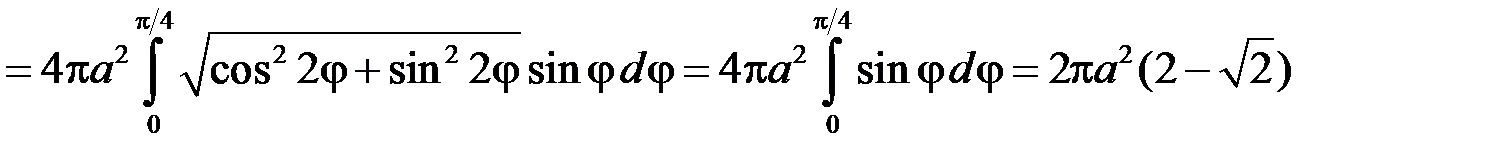 .
.


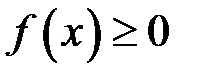 обертається навколо відрізка
обертається навколо відрізка 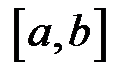 осі
осі 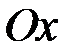 . Тоді площа поверхні утвореного таким чином тіла знаходиться за формулою:
. Тоді площа поверхні утвореного таким чином тіла знаходиться за формулою: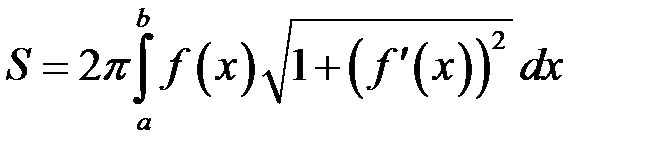 . (17.1)
. (17.1)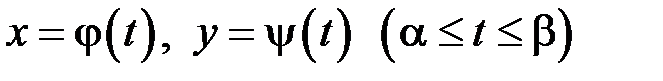 , де
, де 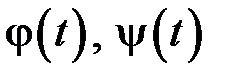 – неперервно диференційовні на відрізку
– неперервно диференційовні на відрізку 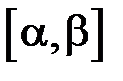 функції, причому
функції, причому 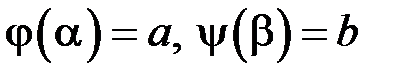 , то
, то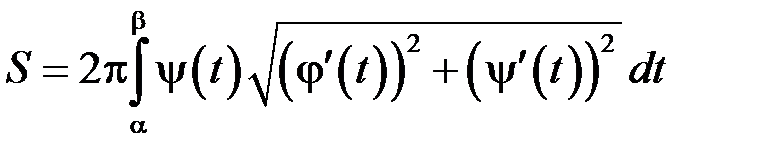 . (17.2)
. (17.2)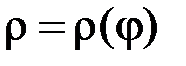 ,
, 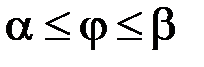 , то площа поверхні тіла, яке утворено обертанням фігури, обмеженої графіком функції
, то площа поверхні тіла, яке утворено обертанням фігури, обмеженої графіком функції 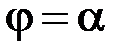 ,
, 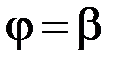 навколо полярної осі, дорівнює:
навколо полярної осі, дорівнює: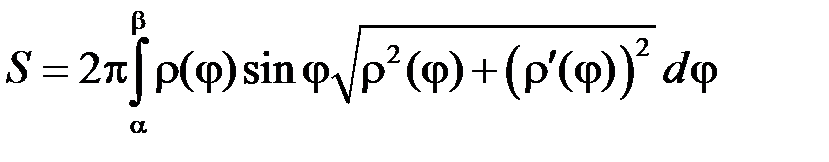 . (17.3)
. (17.3) дуги параболи
дуги параболи 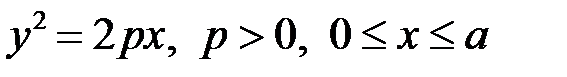 (рис. 21).
(рис. 21).
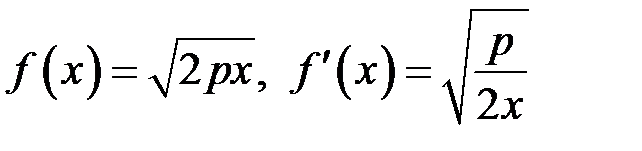 ,
,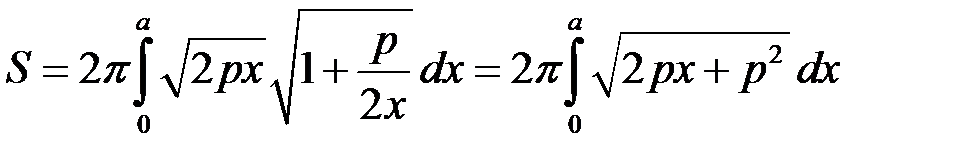
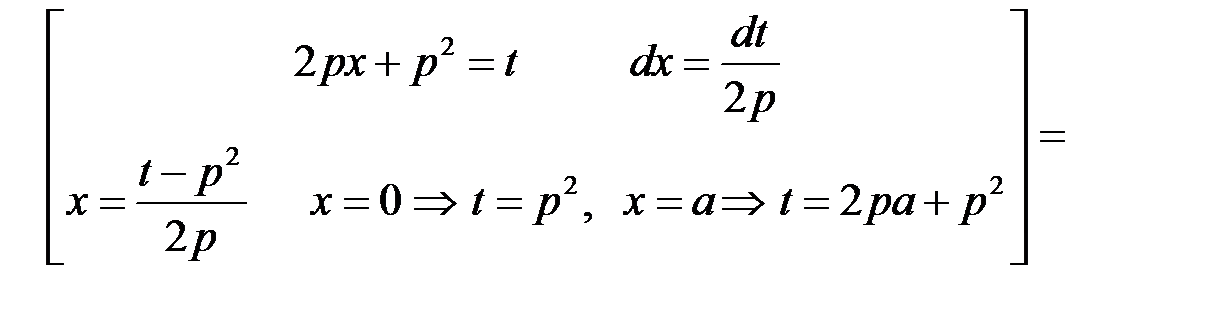
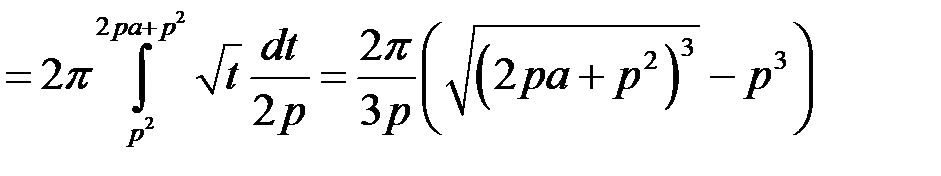 .
.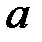 і
і 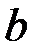 (
( 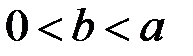 ).
).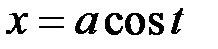 ,
, 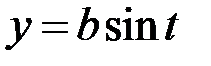 . Введемо до розгляду ексцентриситет еліпса:
. Введемо до розгляду ексцентриситет еліпса: 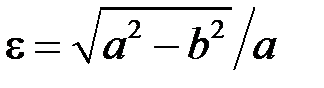 . Шукану площу можна отримати як подвоєну площу поверхні тіла, утвореного обертанням чверті еліпса, розташованої у 1-му квадранті, навколо осі
. Шукану площу можна отримати як подвоєну площу поверхні тіла, утвореного обертанням чверті еліпса, розташованої у 1-му квадранті, навколо осі  . Отже згідно з формулою (17.2) маємо:
. Отже згідно з формулою (17.2) маємо: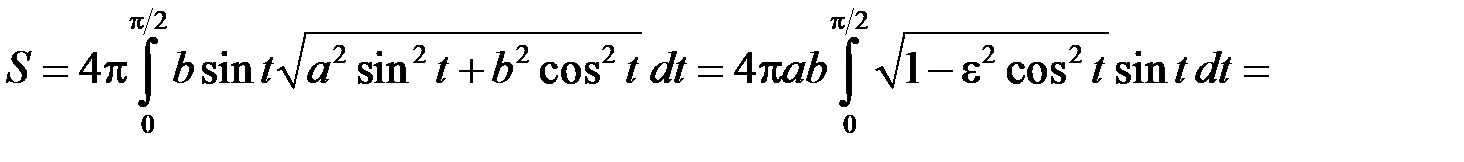
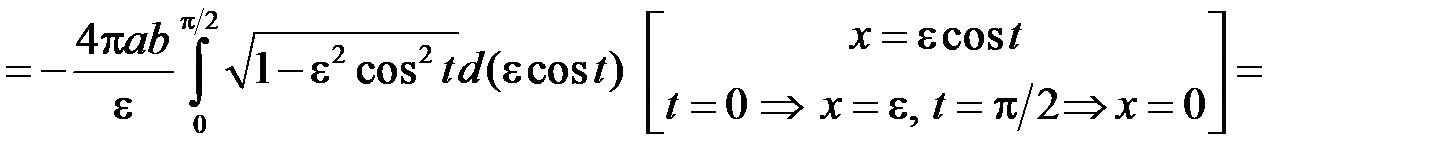
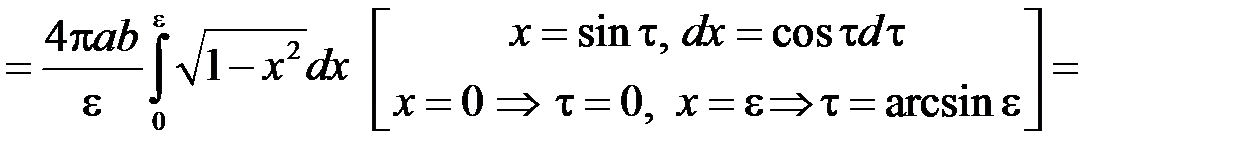
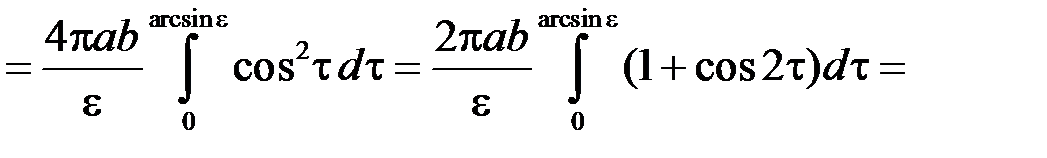
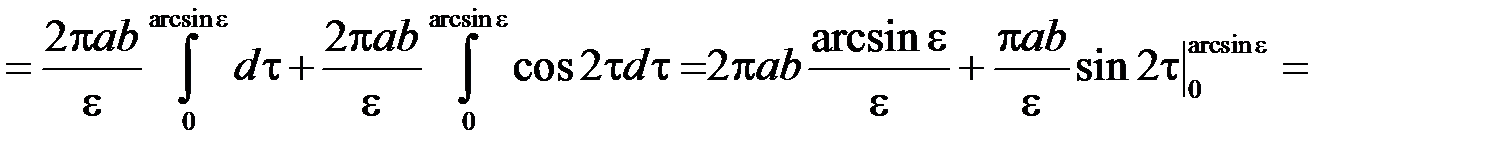
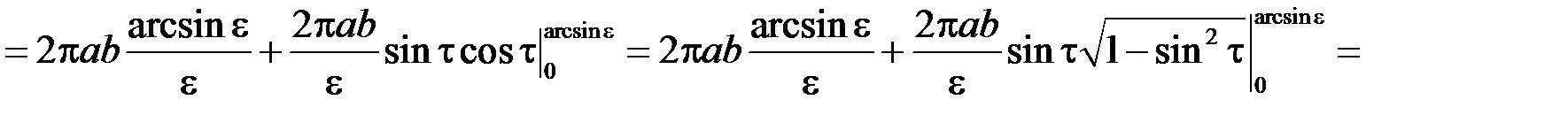
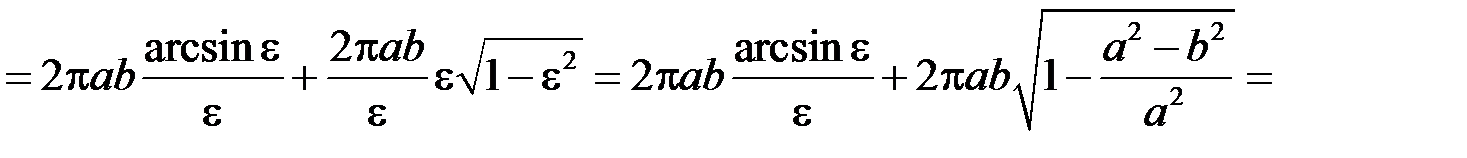
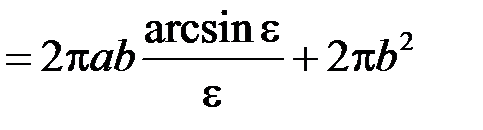 .
. (
( 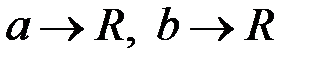 ) отримується формула площі поверхні сфери радіуса
) отримується формула площі поверхні сфери радіуса  :
: 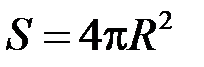 .
.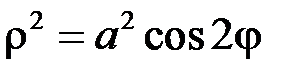 навколо полярної осі.
навколо полярної осі.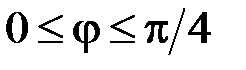 . Згідно з формулою (17.3) маємо:
. Згідно з формулою (17.3) маємо: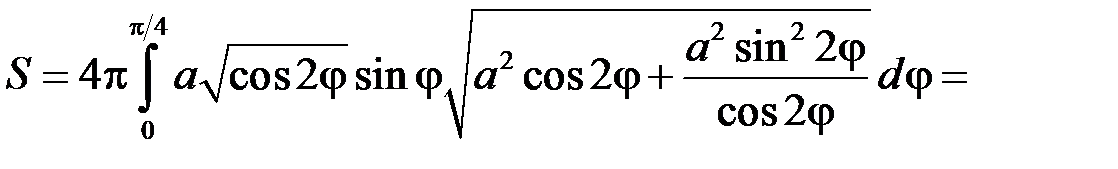
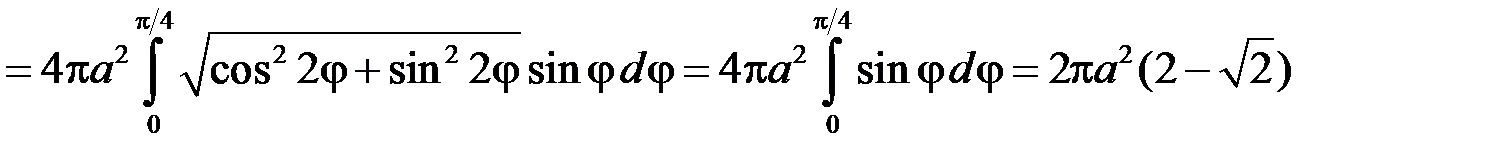 .
.