Припустимо, що треба визначити деяку сталу величину  (геометричну, фізичну, або якусь іншу), яка пов’язана з проміжком
(геометричну, фізичну, або якусь іншу), яка пов’язана з проміжком 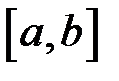 . При цьому припускається наступне.
. При цьому припускається наступне.
Розіб’ємо відрізок 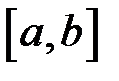 точками ділення на частинні відрізки
точками ділення на частинні відрізки 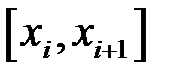
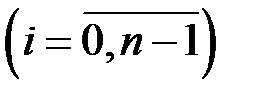 . Тоді відповідним чином розбивається і величина
. Тоді відповідним чином розбивається і величина  , тобто кожному з відрізків
, тобто кожному з відрізків 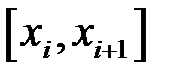
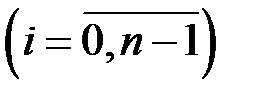 відповідає величина
відповідає величина 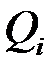
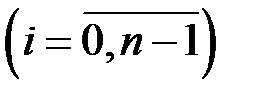 , і виконана рівність:
, і виконана рівність:
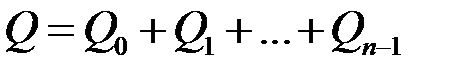 .
.
Легко помітити, що всі величини, які ми обчислювали у п.8 (площа фігури, довжина дуги, об’єм тіла) задовольняють це припущення.
Така властивість величини  називається адитивністю.
називається адитивністю.
Схема застосування визначеного інтеграла до задач механіки і фізики (як, власне, і геометрії) полягає у наступному: розглянемо деякий елементарний відрізок 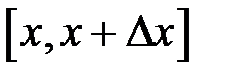 довжини
довжини 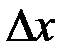 , що належить відрізку
, що належить відрізку 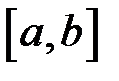 . Цьому проміжку відповідає елемент
. Цьому проміжку відповідає елемент 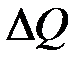 величини
величини  . Виходячи з умов задачі, намагаються знайти для
. Виходячи з умов задачі, намагаються знайти для 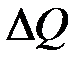 наближений вираз
наближений вираз 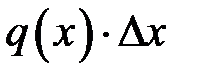 , який лінійний відносно
, який лінійний відносно 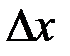 , тобто віділяють з
, тобто віділяють з 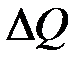 його головну частину – диференціал
його головну частину – диференціал 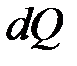 .
.
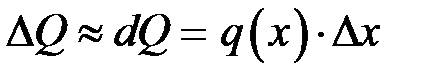
Відносна помилка цієї наближеної рівності, а саме величина 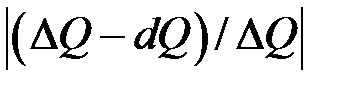 прямує до нуля разом з
прямує до нуля разом з 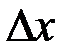 .
.
Тоді кожному з частинних проміжків 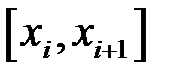 буде відповідати наближене значення
буде відповідати наближене значення 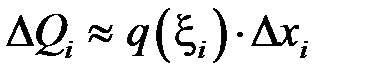 ,
, 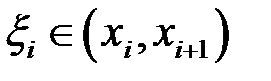 . І шукана величина
. І шукана величина  наближено буде дорівнювати:
наближено буде дорівнювати:
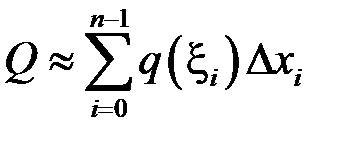 .
.
Права частина цієї рівності – інтегральна сума для функції 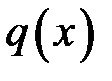 . Отже точне значення величини
. Отже точне значення величини  може бути подано інтегралом
може бути подано інтегралом
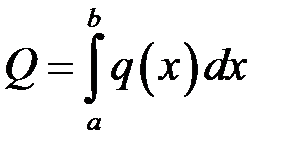 . (18.1)
. (18.1)
Можна виходити також з рівностей 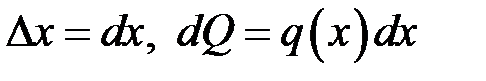 , інтегруючи останню рівність у межах від
, інтегруючи останню рівність у межах від 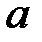 до
до 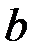 , отримаємо (18.1).
, отримаємо (18.1).
Слід в той же час відмітити, що у реальних фізичних задачах розбиття відрізку 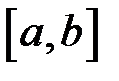 на як завгодно малі відрізки принципово неможливо. Справа у тому, що величини цих відрізків залежать від конкретних умов. Наприклад, внаслідок атомістичної структури речовини ця величина не може бути зробленою меншою, ніж деяка задана величина. А тому граничний перехід при
на як завгодно малі відрізки принципово неможливо. Справа у тому, що величини цих відрізків залежать від конкретних умов. Наприклад, внаслідок атомістичної структури речовини ця величина не може бути зробленою меншою, ніж деяка задана величина. А тому граничний перехід при 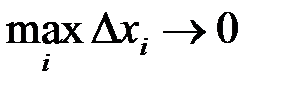 не може бути виконано до кінця. Це означає, що точна рівність (18.1) – деяка ідеалізація. Фактично в фізичних задачах під інтегралом розуміється не границя послідовності інтегральних сум, а сума великого числа достатньо малих доданків.
не може бути виконано до кінця. Це означає, що точна рівність (18.1) – деяка ідеалізація. Фактично в фізичних задачах під інтегралом розуміється не границя послідовності інтегральних сум, а сума великого числа достатньо малих доданків.
1. Обчислення пройденого шляху.
Нехай точка 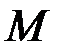 рухається вздовж деякої осі, і миттєва швидкість цієї точки у момент часу
рухається вздовж деякої осі, і миттєва швидкість цієї точки у момент часу 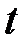 дорівнює
дорівнює 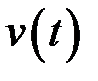 . Треба знайти шлях, який пройде точка від моменту часу
. Треба знайти шлях, який пройде точка від моменту часу 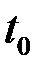 до моменту
до моменту 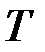 .
.
Якби швидкість була сталою величиною ( 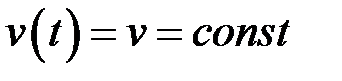 ), така задача розв’язувалась би дуже просто:
), така задача розв’язувалась би дуже просто: 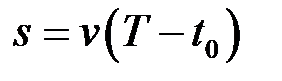 . Але
. Але 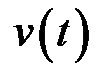 – змінна величина.
– змінна величина.
Розіб’ємо відрізок 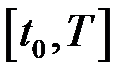 на частинні
на частинні 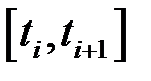
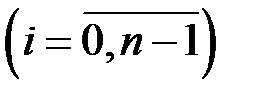 і в кожному з них оберемо довільну точку (момент часу)
і в кожному з них оберемо довільну точку (момент часу) 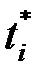 . Відрізки ці можна обрати настільки малими, що швидкість за цей малий проміжок часу
. Відрізки ці можна обрати настільки малими, що швидкість за цей малий проміжок часу 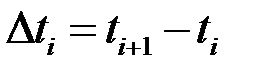 не встигає суттєво змінитися, і тоді на кожному з відрізків швидкість наближено можна вважати сталою. І тоді шлях, пройдений точкою за цей проміжок часу наближено дорівнює
не встигає суттєво змінитися, і тоді на кожному з відрізків швидкість наближено можна вважати сталою. І тоді шлях, пройдений точкою за цей проміжок часу наближено дорівнює 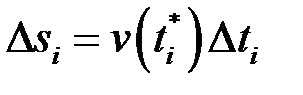 , а весь шлях:
, а весь шлях:
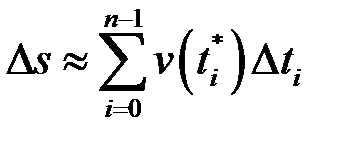 .
.
Переходячи тепер до границі при 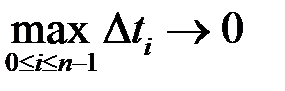 , отримаємо:
, отримаємо:
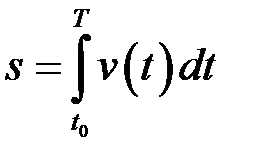 . (18.2)
. (18.2)
Приклад. Миттєва швидкість точки 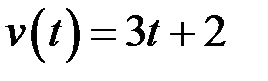 . Знайти шлях, який точка пройшла від моменту часу
. Знайти шлях, який точка пройшла від моменту часу 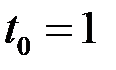 до
до 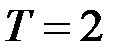 .
.
Згідно з формулою (18.2) маємо:
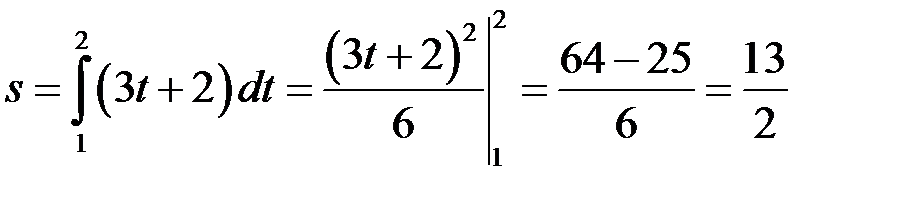 .
.
2. Обчислення роботи сили.
У п. 2 ми визначили, що робота 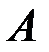 сили
сили 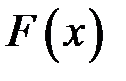 , що діє вздовж напряму руху на відрізку
, що діє вздовж напряму руху на відрізку 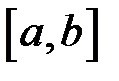 , обчислюється за формулою
, обчислюється за формулою
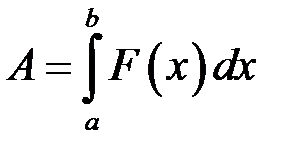 . (18.3)
. (18.3)
Приклад 1. Обчислити роботу, яку треба затратити, щоб тіло маси 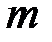 підняти з поверхні Землі вертикально вгору на висоту
підняти з поверхні Землі вертикально вгору на висоту 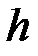 , якщо середній радіус Землі дорівнює
, якщо середній радіус Землі дорівнює 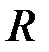 .
.
Згідно з законом Ньютона, сила 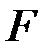 притягання тіла Землею дорівнює:
притягання тіла Землею дорівнює:
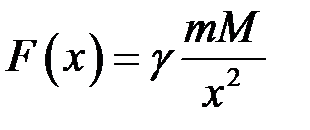 ,
,
де 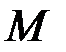 – маса Землі,
– маса Землі, 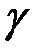 – гравітаційна стала,
– гравітаційна стала, 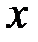 – відстань від центра тіла до центра Землі (рис. 22).
– відстань від центра тіла до центра Землі (рис. 22).
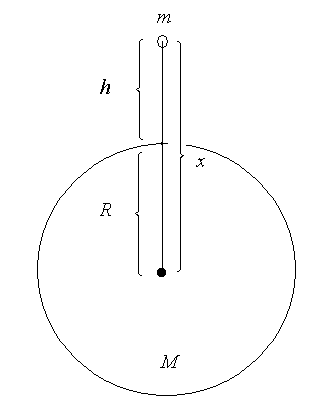
Рис. 22.
Якщо 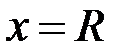 , тобто тіло знаходиться на поверхні Землі, то
, тобто тіло знаходиться на поверхні Землі, то 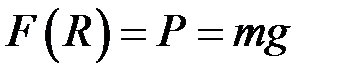 – вага тіла, тобто:
– вага тіла, тобто:
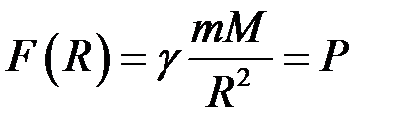 .
.
Звідси:
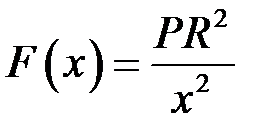 .
.
За формулою (18.3) маємо:
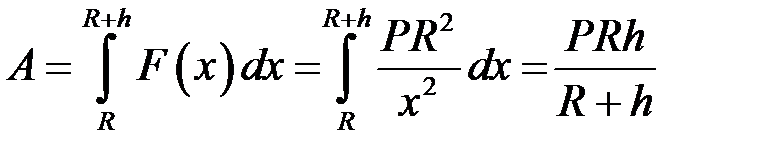 .
.
Приклад 2. Знайти роботу, яку треба витратити, щоб викачати воду з резервуару, що має форму прямого кругового циліндра з радіусом основи 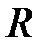 та висотою
та висотою 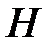 .
.
За один цикл роботи насосу рівень води, що знаходиться на відстані 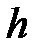 від верхньої основи резервуару під дією сили тяжіння
від верхньої основи резервуару під дією сили тяжіння 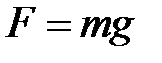 знизився на величину
знизився на величину 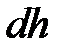 (рис. 23).
(рис. 23).
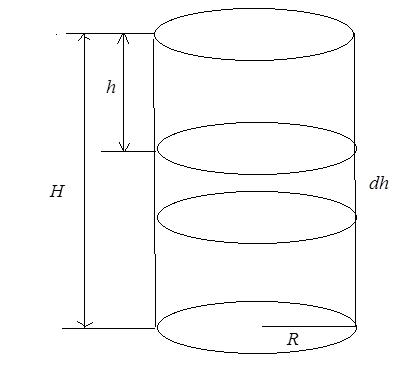
Рис. 23.
При переміщенні шару води товщиною 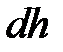 на відстань
на відстань 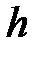 виконується робота:
виконується робота:
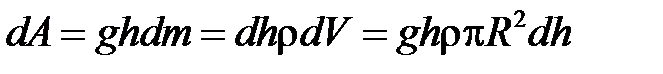 .
.
Інтегруючи цю рівність у межах від 0 до 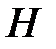 , отримаємо шукану роботу:
, отримаємо шукану роботу:
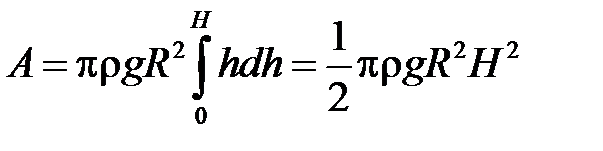 .
.
Приклад 3. Знайти роботу, яку треба витратити, щоб викачати воду з конічного резервуару, оберненого вершиною вниз. Радіус основи конуса  , а висота
, а висота 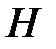 .
.
Задача відрізняється від попередньої лише тим, що інакше буде обчислюватися елемент об’єму 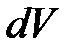 . У цьому випадку (рис. 24):
. У цьому випадку (рис. 24):
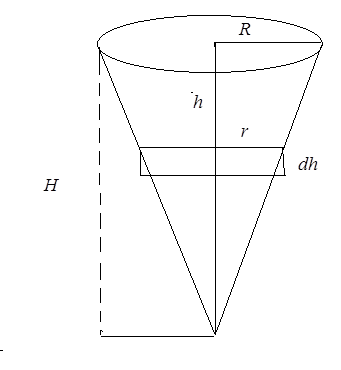
Рис. 24.
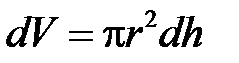 , де
, де
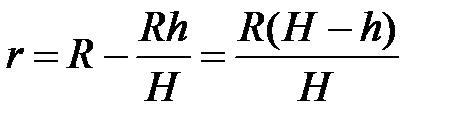 .
.
Тоді аналогічно попередній задачі маємо:
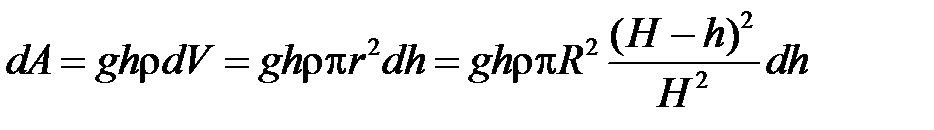 .
.
Інтегруючи цю рівність у межах від 0 до 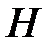 , отримуємо:
, отримуємо:
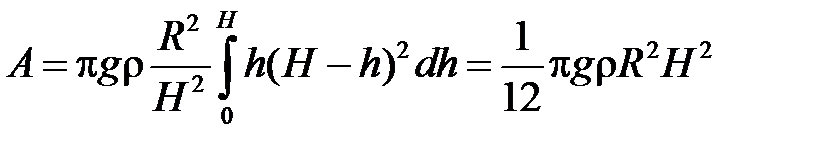 .
.
3. Обчислення маси і координати центру ваги неоднорідного стрижня.
Розглянемо неоднорідний стрижень, розташований на відрізку 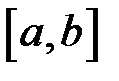 осі
осі 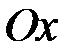 (рис. 25) .
(рис. 25) .
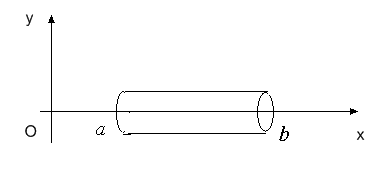
Рис. 25.
Нехай 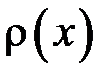 – лінійна густина стрижня у точці з координатою
– лінійна густина стрижня у точці з координатою 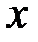
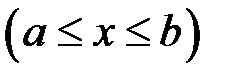 . Треба знайти масу стрижня.
. Треба знайти масу стрижня.
Виділимо на 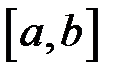 елементарний відрізок
елементарний відрізок 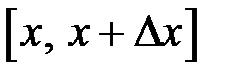 . Тоді елемент маси
. Тоді елемент маси 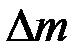 на цьому відрізку наближено дорівнює
на цьому відрізку наближено дорівнює
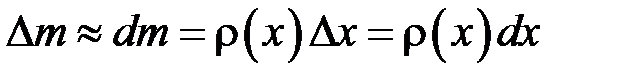 .
.
Інтегруючи в межах від 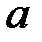 до
до 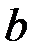 , дістаємо:
, дістаємо:
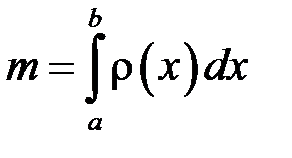 . (18.4)
. (18.4)
Для обчислення координати центра ваги стрижня користуються формулою:
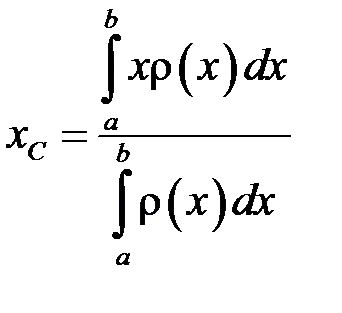 . (18.5)
. (18.5)
Приклад. Обчислити масу і координату центра ваги стрижня, розташованого на відрізку 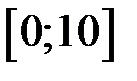 , якщо його лінійна густина
, якщо його лінійна густина
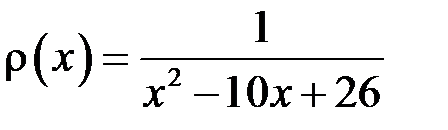 .
.
Згідно з формулою (18.4) маємо:
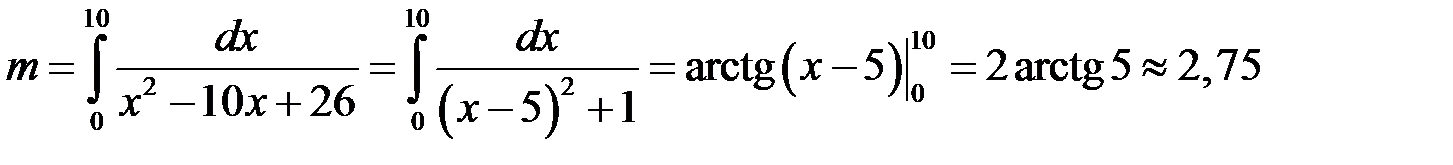 .
.
Згідно з формулою (18.5):
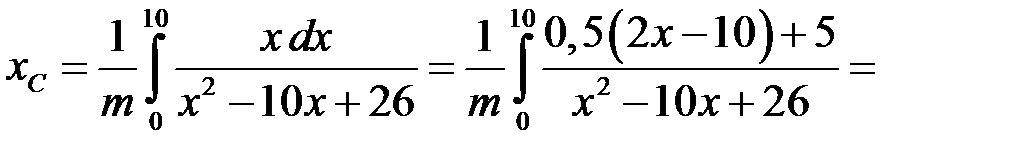
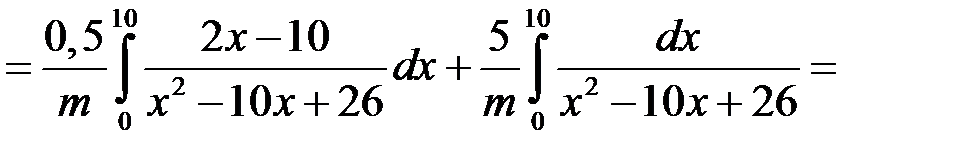
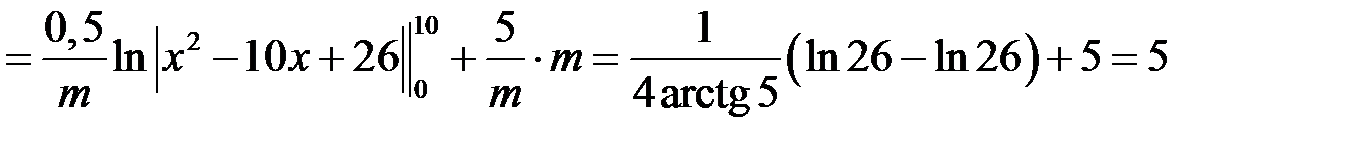 .
.
1. Обчислення тиску рідини на вертикально занурену пластину.
Розглянемо вертикальну пластину, яку занурено у рідину на глибині 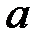 . Введемо систему координат
. Введемо систему координат 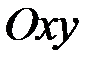 , причому вісь
, причому вісь 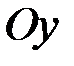 напрямимо горизонтально по поверхні рідини, а вісь
напрямимо горизонтально по поверхні рідини, а вісь 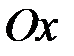 – вертикально вниз. Пластину будемо вважати плоскою фігурою, обмеженою лініями
– вертикально вниз. Пластину будемо вважати плоскою фігурою, обмеженою лініями 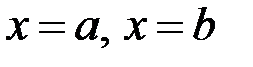 і графіками функцій
і графіками функцій 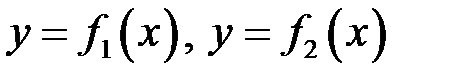 (рис. 26).
(рис. 26).
Треба знайти повний гідростатичний тиск на пластину. Згідно з законом Паскаля[3] тиск 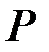 рідини на горизонтальну площадку дорівнює:
рідини на горизонтальну площадку дорівнює:
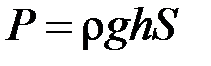 ,
,
де 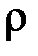 – густина рідини,
– густина рідини, 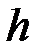 – глибина занурення,
– глибина занурення, 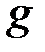 – прискорення вільного падіння,
– прискорення вільного падіння, 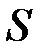 – площа пластини. Якщо пластина вертикальна, то її різні точки лежатимуть на різних глибинах, і цією формулою безпосередньо користува-
– площа пластини. Якщо пластина вертикальна, то її різні точки лежатимуть на різних глибинах, і цією формулою безпосередньо користува-
тися не можна. Виділимо елементарну площадку шириною 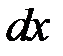 , яка лежить на глибині
, яка лежить на глибині 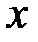 ; наближено її можна вважати прямокутною за рахунок малості величини
; наближено її можна вважати прямокутною за рахунок малості величини 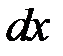 , тоді її елементарна площа:
, тоді її елементарна площа:
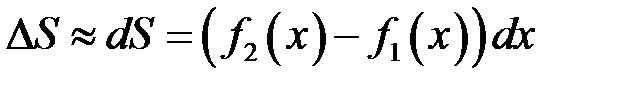 .
.
Елементарний тиск на цю площадку дорівнює
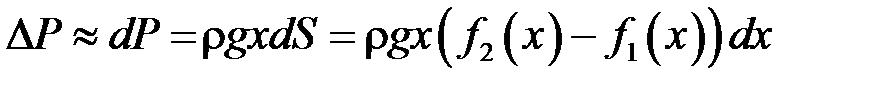 .
.
Інтегруючи в межах від 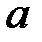 до
до 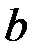 , дістаємо шуканий тиск на всю пластину:
, дістаємо шуканий тиск на всю пластину:
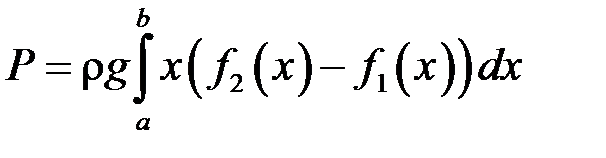 . (18.6)
. (18.6)
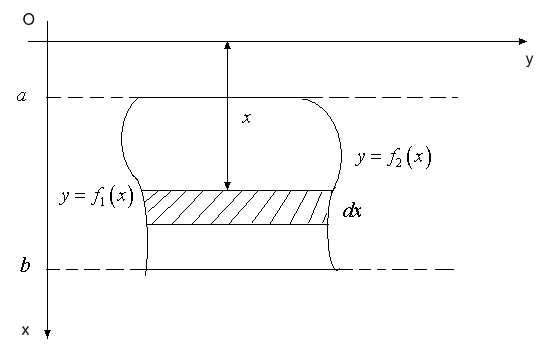
Рис. 26.
Розглянемо приклади.
Приклад 1. Нехай пластина має формі напівкруга радіуса 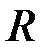 , і діаметр круга знаходиться на поверхні рідини (рис. 27).
, і діаметр круга знаходиться на поверхні рідини (рис. 27).
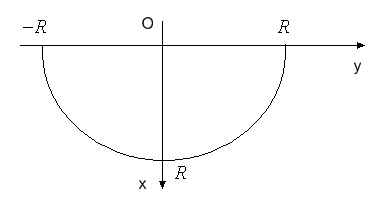
Рис. 27.
Легко дістаємо: 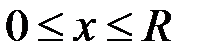 ,
, 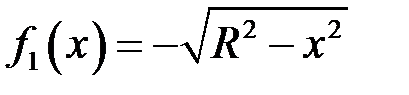 ,
, 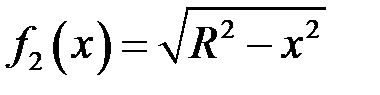 , і згідно з формулою (18.6):
, і згідно з формулою (18.6):
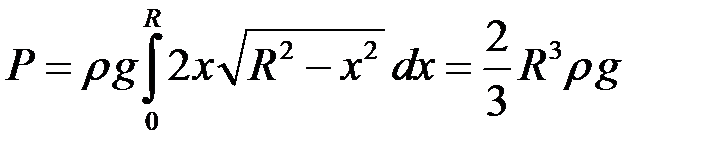
(обчислення інтеграла перевірте самостійно).
Приклад 2. Нехай пластина має форму рівнобедреного трикутника з основою 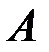 і бічними сторонами, довжина яких дорівнює
і бічними сторонами, довжина яких дорівнює 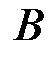 , причому основа знаходиться на поверхні рідини (рис. 28).
, причому основа знаходиться на поверхні рідини (рис. 28).
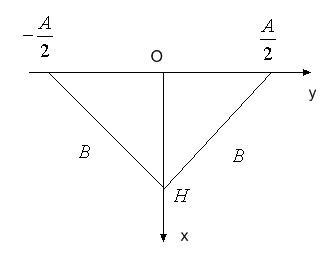
Рис. 28.
Легко зрозуміти, що у цьому випадку 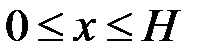 , де
, де
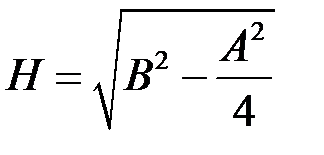 .
.
Далі:
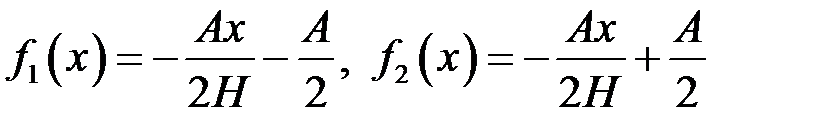 ,
,
і згідно з формулою (18.6) матимемо:
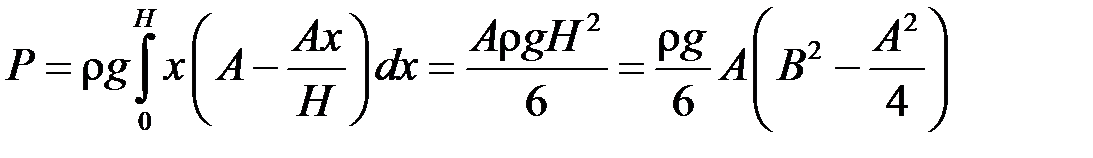
(обчислення інтеграла перевірте самостійно).
2. Обчислення часу витікання рідини з отвору.
Розглянемо резервуар, що має форму тіла, утвореного обертанням графіка функції 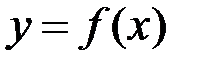 навколо відрізку
навколо відрізку 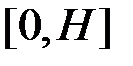 осі
осі 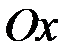 , причому вісь
, причому вісь 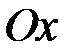 напрямимо вертикально вниз,а вісь
напрямимо вертикально вниз,а вісь 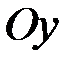 – горизонтально вправо (рис. 29). В дні цього резервуару є круглий отвір радіусу
– горизонтально вправо (рис. 29). В дні цього резервуару є круглий отвір радіусу 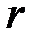 . Треба обчислити, за який час рідина, яка цілком заповнює резервуар, вся витече через цей отвір.
. Треба обчислити, за який час рідина, яка цілком заповнює резервуар, вся витече через цей отвір.
Скористаємось формулою Торрічеллі[4], яка виражає швидкість 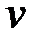 витікання рідини з отвору в резервуарі, що знаходиться на відстані
витікання рідини з отвору в резервуарі, що знаходиться на відстані 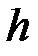 нижче рівня рідини:
нижче рівня рідини:
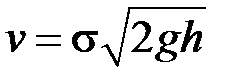 , де
, де 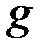 – прискорення вільного падіння, а
– прискорення вільного падіння, а  – коефіцієнт, який залежить від властивостей рідини (для води
– коефіцієнт, який залежить від властивостей рідини (для води 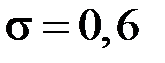 ).
).
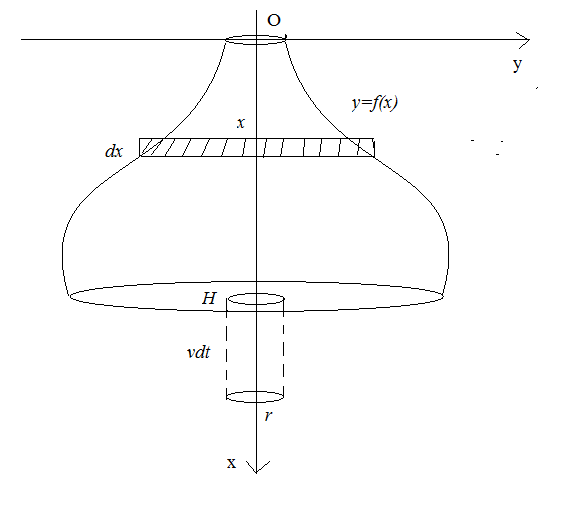
Рис. 29.
Нехай 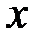 – довільна точка відрізку
– довільна точка відрізку 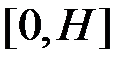 . Припустимо, що за час
. Припустимо, що за час 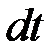 рівень рідини у резервуарі за рахунок витікання з отвору змінився з на величину
рівень рідини у резервуарі за рахунок витікання з отвору змінився з на величину 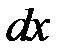 . Знайдемо об’єм рідини, що витекла за час
. Знайдемо об’єм рідини, що витекла за час 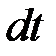 . З одного боку цей об’єм наближено дорівнює об’єму циліндра висотою
. З одного боку цей об’єм наближено дорівнює об’єму циліндра висотою 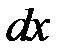 і радіусом
і радіусом 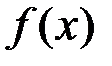 :
:
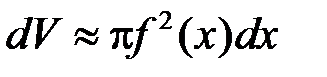 .
.
З іншого боку цей самий об’єм дорівнює об’єму циліндра радіусом 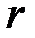 і висотою
і висотою 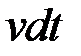 (шлях, пройдений рідиною, що витікає з отвору, за час
(шлях, пройдений рідиною, що витікає з отвору, за час 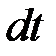 ):
):
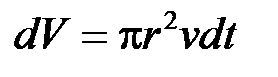 .
.
Тоді з урахуванням формули Торрічеллі, з точністю до величин порядку 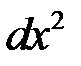 :
:
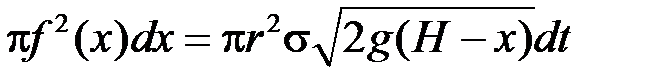 .
.
Або:
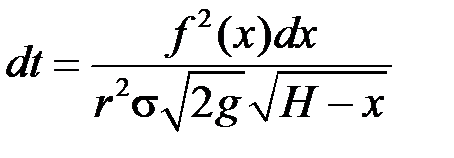 .
.
Інтегруючи цю рівність у межах від 0 до 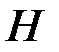 , отримуємо шуканий час:
, отримуємо шуканий час:
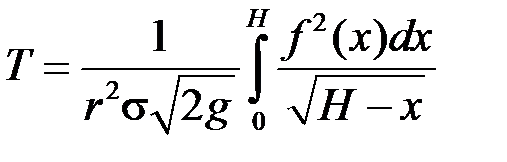 . (18.7)
. (18.7)
Помітимо, що інтеграл у правій частині формули (18.7) є невласним інтегралом II роду, особлива точка 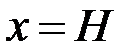 . Треба, щоб цей інтеграл був збіжним.
. Треба, щоб цей інтеграл був збіжним.
Приклад. За який час вода витече з резервуару, що має форму півкулі радіусу 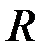 через круглий отвір радіусу
через круглий отвір радіусу 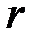 у його дні?
у його дні?
У даному випадку маємо: 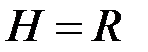 ,
, 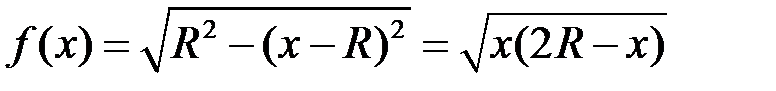 . Згідно з формулою (18.7):
. Згідно з формулою (18.7):
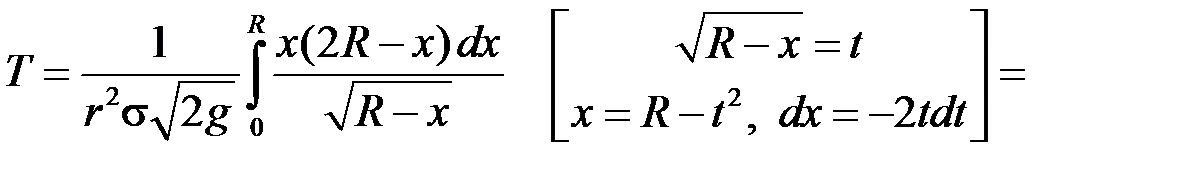
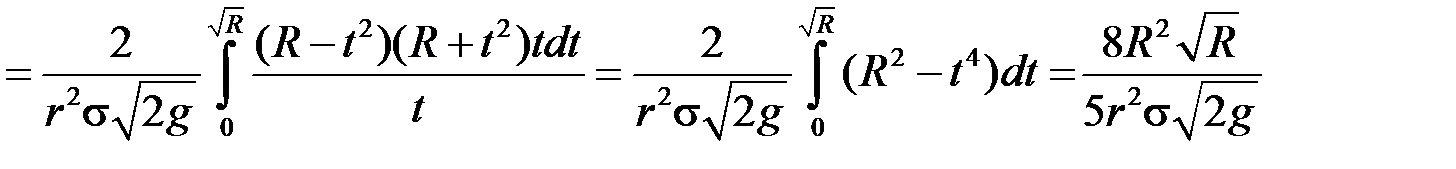 .
.


 (геометричну, фізичну, або якусь іншу), яка пов’язана з проміжком
(геометричну, фізичну, або якусь іншу), яка пов’язана з проміжком 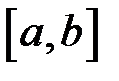 . При цьому припускається наступне.
. При цьому припускається наступне.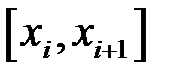
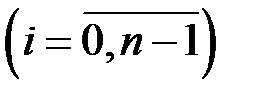 . Тоді відповідним чином розбивається і величина
. Тоді відповідним чином розбивається і величина 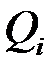
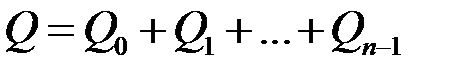 .
.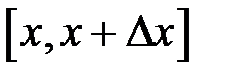 довжини
довжини 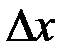 , що належить відрізку
, що належить відрізку 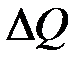 величини
величини 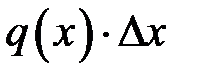 , який лінійний відносно
, який лінійний відносно 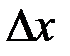 , тобто віділяють з
, тобто віділяють з 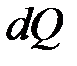 .
.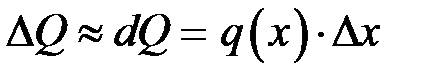
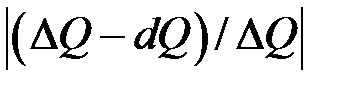 прямує до нуля разом з
прямує до нуля разом з 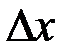 .
.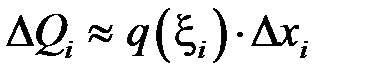 ,
, 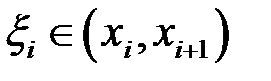 . І шукана величина
. І шукана величина 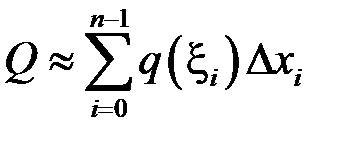 .
.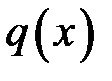 . Отже точне значення величини
. Отже точне значення величини 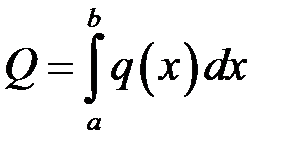 . (18.1)
. (18.1)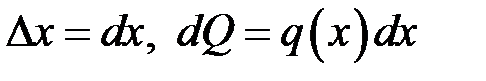 , інтегруючи останню рівність у межах від
, інтегруючи останню рівність у межах від 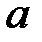 до
до 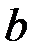 , отримаємо (18.1).
, отримаємо (18.1).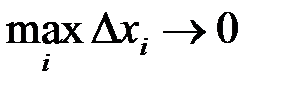 не може бути виконано до кінця. Це означає, що точна рівність (18.1) – деяка ідеалізація. Фактично в фізичних задачах під інтегралом розуміється не границя послідовності інтегральних сум, а сума великого числа достатньо малих доданків.
не може бути виконано до кінця. Це означає, що точна рівність (18.1) – деяка ідеалізація. Фактично в фізичних задачах під інтегралом розуміється не границя послідовності інтегральних сум, а сума великого числа достатньо малих доданків. рухається вздовж деякої осі, і миттєва швидкість цієї точки у момент часу
рухається вздовж деякої осі, і миттєва швидкість цієї точки у момент часу 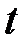 дорівнює
дорівнює 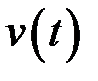 . Треба знайти шлях, який пройде точка від моменту часу
. Треба знайти шлях, який пройде точка від моменту часу 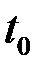 до моменту
до моменту 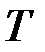 .
.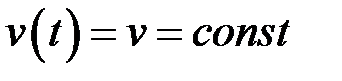 ), така задача розв’язувалась би дуже просто:
), така задача розв’язувалась би дуже просто: 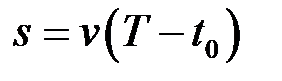 . Але
. Але 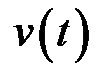 – змінна величина.
– змінна величина.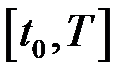 на частинні
на частинні 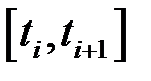
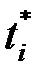 . Відрізки ці можна обрати настільки малими, що швидкість за цей малий проміжок часу
. Відрізки ці можна обрати настільки малими, що швидкість за цей малий проміжок часу 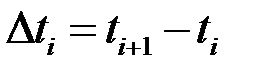 не встигає суттєво змінитися, і тоді на кожному з відрізків швидкість наближено можна вважати сталою. І тоді шлях, пройдений точкою за цей проміжок часу наближено дорівнює
не встигає суттєво змінитися, і тоді на кожному з відрізків швидкість наближено можна вважати сталою. І тоді шлях, пройдений точкою за цей проміжок часу наближено дорівнює 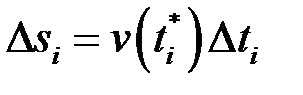 , а весь шлях:
, а весь шлях: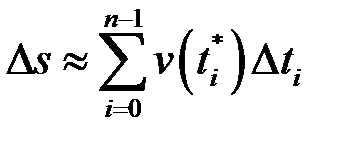 .
.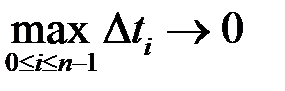 , отримаємо:
, отримаємо: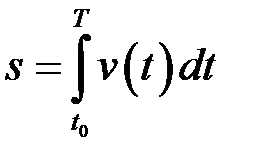 . (18.2)
. (18.2)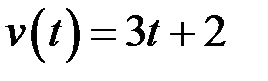 . Знайти шлях, який точка пройшла від моменту часу
. Знайти шлях, який точка пройшла від моменту часу 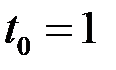 до
до 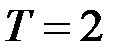 .
.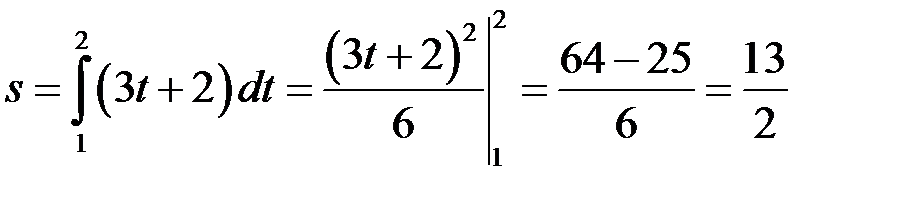 .
.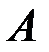 сили
сили 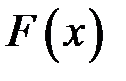 , що діє вздовж напряму руху на відрізку
, що діє вздовж напряму руху на відрізку 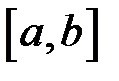 , обчислюється за формулою
, обчислюється за формулою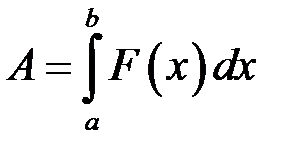 . (18.3)
. (18.3) підняти з поверхні Землі вертикально вгору на висоту
підняти з поверхні Землі вертикально вгору на висоту 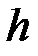 , якщо середній радіус Землі дорівнює
, якщо середній радіус Землі дорівнює 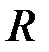 .
.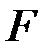 притягання тіла Землею дорівнює:
притягання тіла Землею дорівнює: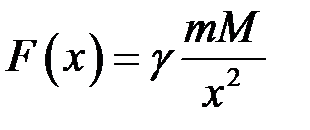 ,
,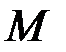 – маса Землі,
– маса Землі, 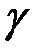 – гравітаційна стала,
– гравітаційна стала, 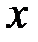 – відстань від центра тіла до центра Землі (рис. 22).
– відстань від центра тіла до центра Землі (рис. 22).
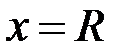 , тобто тіло знаходиться на поверхні Землі, то
, тобто тіло знаходиться на поверхні Землі, то 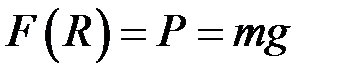 – вага тіла, тобто:
– вага тіла, тобто: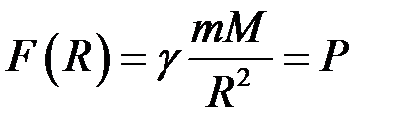 .
.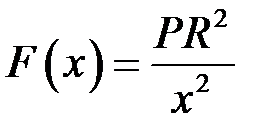 .
.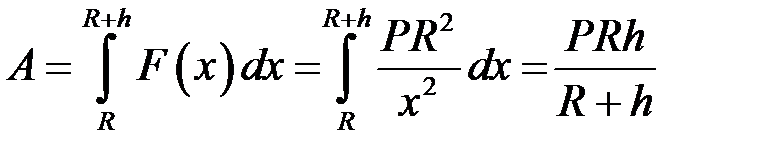 .
.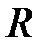 та висотою
та висотою 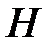 .
.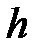 від верхньої основи резервуару під дією сили тяжіння
від верхньої основи резервуару під дією сили тяжіння 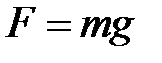 знизився на величину
знизився на величину 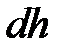 (рис. 23).
(рис. 23).
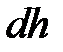 на відстань
на відстань 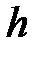 виконується робота:
виконується робота: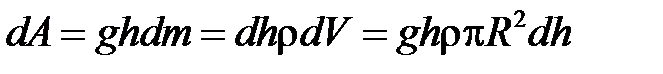 .
.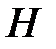 , отримаємо шукану роботу:
, отримаємо шукану роботу: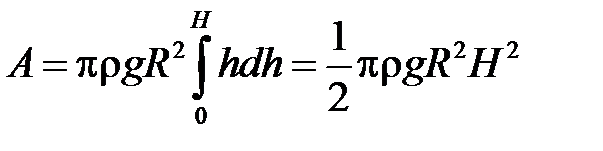 .
. , а висота
, а висота 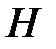 .
.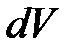 . У цьому випадку (рис. 24):
. У цьому випадку (рис. 24):
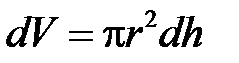 , де
, де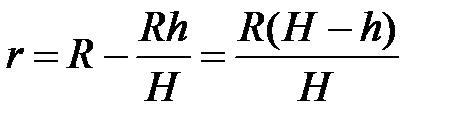 .
.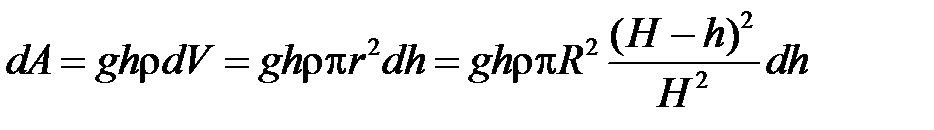 .
.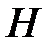 , отримуємо:
, отримуємо: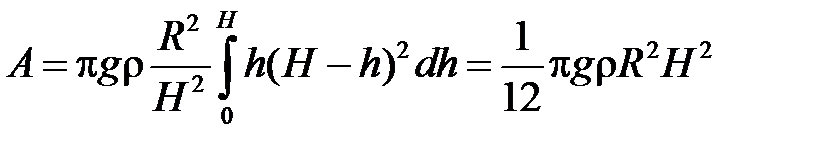 .
. осі
осі 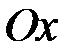 (рис. 25) .
(рис. 25) .
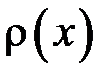 – лінійна густина стрижня у точці з координатою
– лінійна густина стрижня у точці з координатою 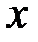
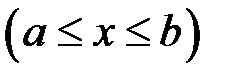 . Треба знайти масу стрижня.
. Треба знайти масу стрижня.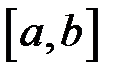 елементарний відрізок
елементарний відрізок 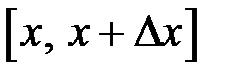 . Тоді елемент маси
. Тоді елемент маси 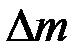 на цьому відрізку наближено дорівнює
на цьому відрізку наближено дорівнює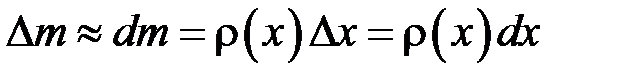 .
.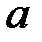 до
до 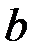 , дістаємо:
, дістаємо: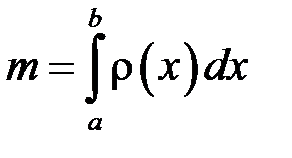 . (18.4)
. (18.4)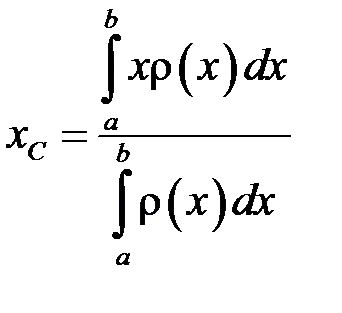 . (18.5)
. (18.5)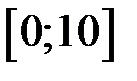 , якщо його лінійна густина
, якщо його лінійна густина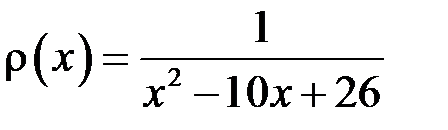 .
.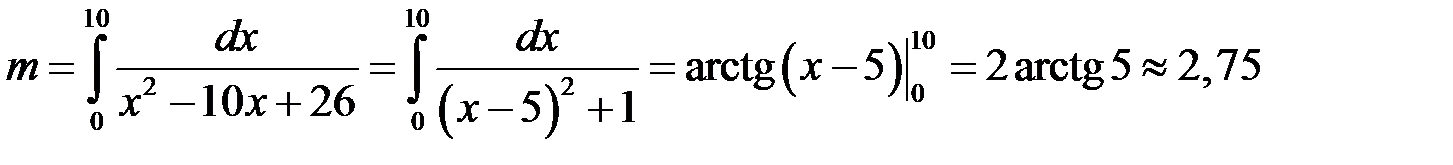 .
.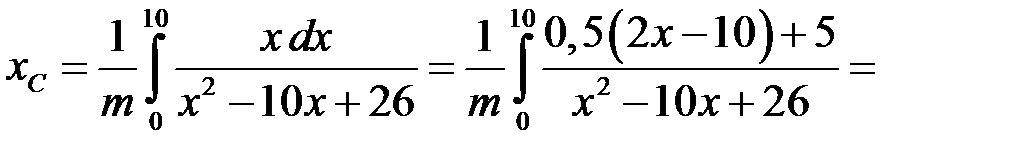
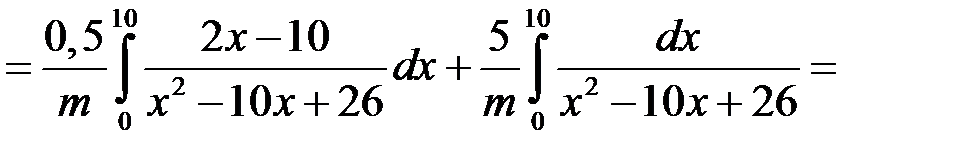
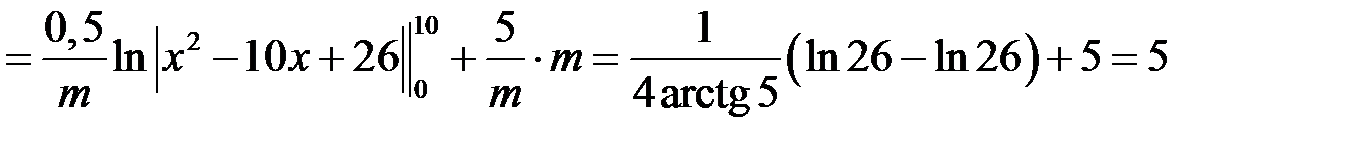 .
.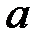 . Введемо систему координат
. Введемо систему координат 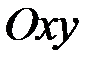 , причому вісь
, причому вісь 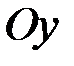 напрямимо горизонтально по поверхні рідини, а вісь
напрямимо горизонтально по поверхні рідини, а вісь 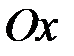 – вертикально вниз. Пластину будемо вважати плоскою фігурою, обмеженою лініями
– вертикально вниз. Пластину будемо вважати плоскою фігурою, обмеженою лініями 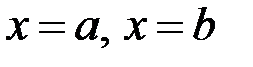 і графіками функцій
і графіками функцій 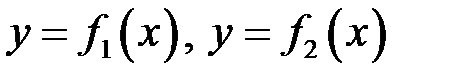 (рис. 26).
(рис. 26). рідини на горизонтальну площадку дорівнює:
рідини на горизонтальну площадку дорівнює: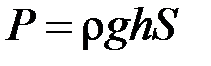 ,
,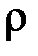 – густина рідини,
– густина рідини, 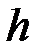 – глибина занурення,
– глибина занурення, 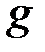 – прискорення вільного падіння,
– прискорення вільного падіння, 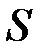 – площа пластини. Якщо пластина вертикальна, то її різні точки лежатимуть на різних глибинах, і цією формулою безпосередньо користува-
– площа пластини. Якщо пластина вертикальна, то її різні точки лежатимуть на різних глибинах, і цією формулою безпосередньо користува-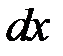 , яка лежить на глибині
, яка лежить на глибині 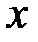 ; наближено її можна вважати прямокутною за рахунок малості величини
; наближено її можна вважати прямокутною за рахунок малості величини 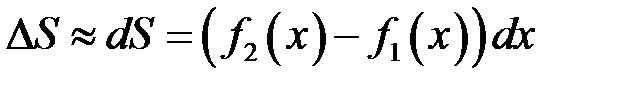 .
.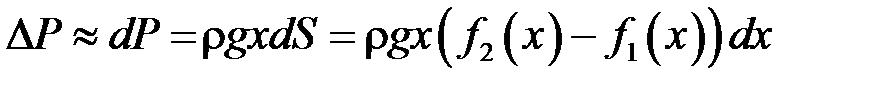 .
.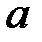 до
до 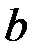 , дістаємо шуканий тиск на всю пластину:
, дістаємо шуканий тиск на всю пластину: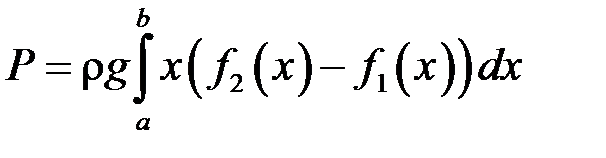 . (18.6)
. (18.6)
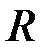 , і діаметр круга знаходиться на поверхні рідини (рис. 27).
, і діаметр круга знаходиться на поверхні рідини (рис. 27).
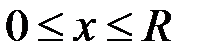 ,
, 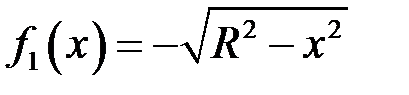 ,
, 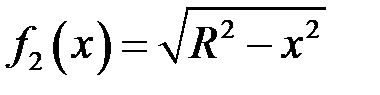 , і згідно з формулою (18.6):
, і згідно з формулою (18.6):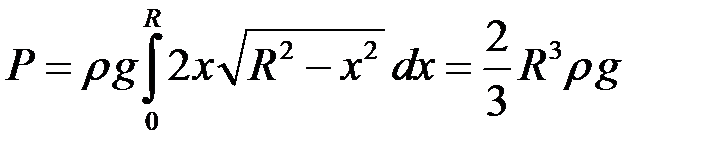
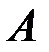 і бічними сторонами, довжина яких дорівнює
і бічними сторонами, довжина яких дорівнює 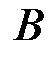 , причому основа знаходиться на поверхні рідини (рис. 28).
, причому основа знаходиться на поверхні рідини (рис. 28).
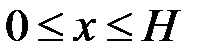 , де
, де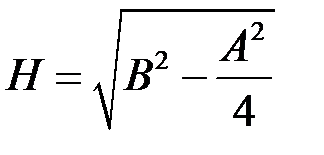 .
.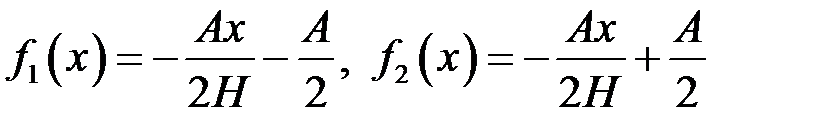 ,
,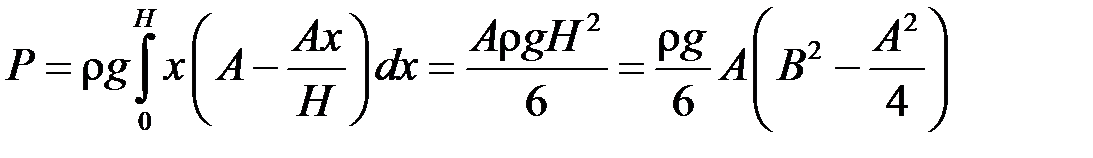
 навколо відрізку
навколо відрізку  осі
осі 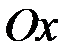 , причому вісь
, причому вісь 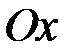 напрямимо вертикально вниз,а вісь
напрямимо вертикально вниз,а вісь 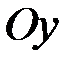 – горизонтально вправо (рис. 29). В дні цього резервуару є круглий отвір радіусу
– горизонтально вправо (рис. 29). В дні цього резервуару є круглий отвір радіусу 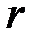 . Треба обчислити, за який час рідина, яка цілком заповнює резервуар, вся витече через цей отвір.
. Треба обчислити, за який час рідина, яка цілком заповнює резервуар, вся витече через цей отвір.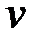 витікання рідини з отвору в резервуарі, що знаходиться на відстані
витікання рідини з отвору в резервуарі, що знаходиться на відстані 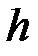 нижче рівня рідини:
нижче рівня рідини: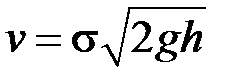 , де
, де 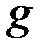 – прискорення вільного падіння, а
– прискорення вільного падіння, а  – коефіцієнт, який залежить від властивостей рідини (для води
– коефіцієнт, який залежить від властивостей рідини (для води 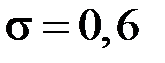 ).
).
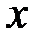 – довільна точка відрізку
– довільна точка відрізку 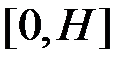 . Припустимо, що за час
. Припустимо, що за час 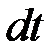 рівень рідини у резервуарі за рахунок витікання з отвору змінився з на величину
рівень рідини у резервуарі за рахунок витікання з отвору змінився з на величину 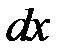 . Знайдемо об’єм рідини, що витекла за час
. Знайдемо об’єм рідини, що витекла за час 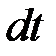 . З одного боку цей об’єм наближено дорівнює об’єму циліндра висотою
. З одного боку цей об’єм наближено дорівнює об’єму циліндра висотою 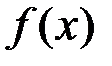 :
: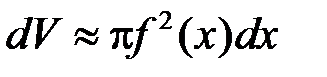 .
.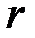 і висотою
і висотою 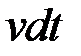 (шлях, пройдений рідиною, що витікає з отвору, за час
(шлях, пройдений рідиною, що витікає з отвору, за час 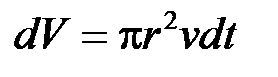 .
.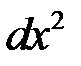 :
: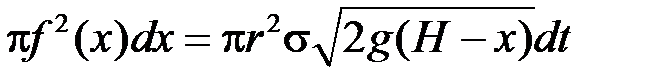 .
.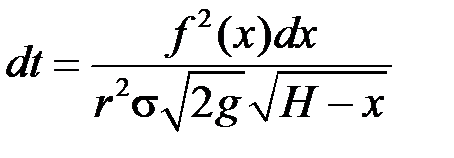 .
.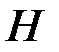 , отримуємо шуканий час:
, отримуємо шуканий час: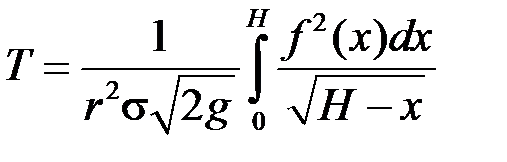 . (18.7)
. (18.7)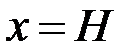 . Треба, щоб цей інтеграл був збіжним.
. Треба, щоб цей інтеграл був збіжним.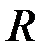 через круглий отвір радіусу
через круглий отвір радіусу 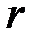 у його дні?
у його дні?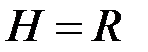 ,
, 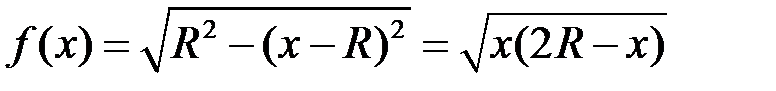 . Згідно з формулою (18.7):
. Згідно з формулою (18.7):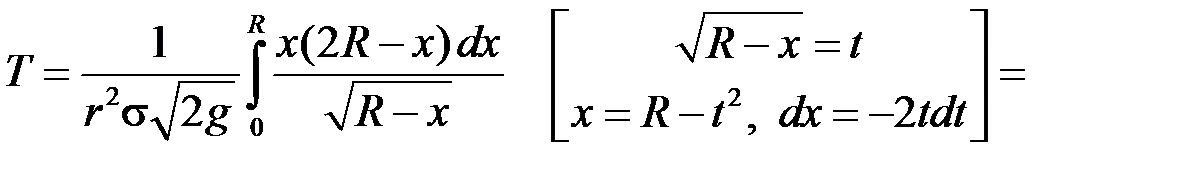
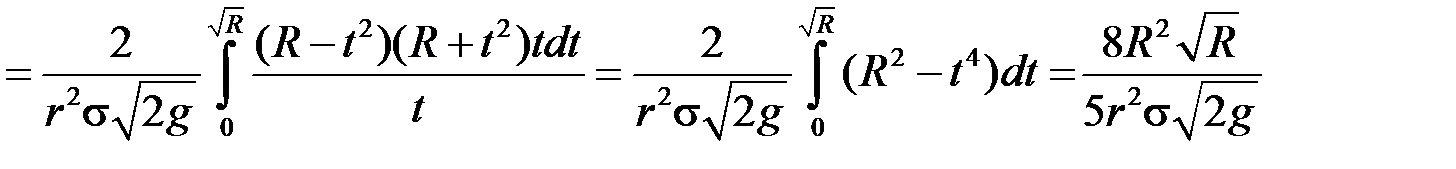 .
.