Ознаки збіжності невласних інтегралів. III.

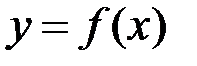Теорема 8(ознака Діріхле). Нехай функція неперервна, а функція 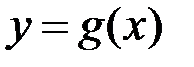має неперервну похідну на проміжку 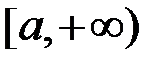, і виконано наступні умови:

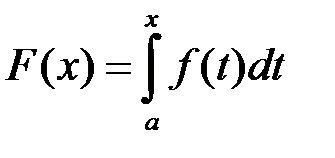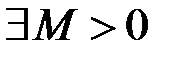
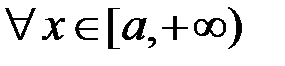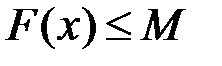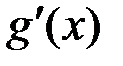1) функція обмежена на , тобто : ;

2) функція зберігає свій знак на 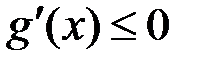, тобто або ;

3) .

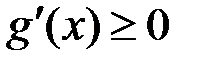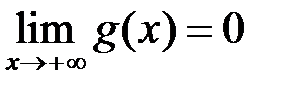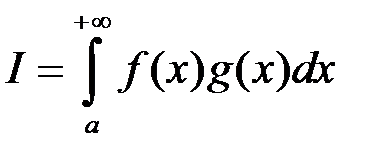Тоді інтеграл збігається.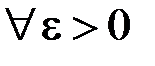

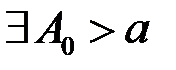
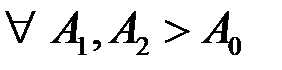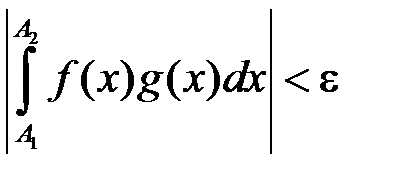Доведення. Скористаємось критерієм Коші, а саме покажемо, що : . Інтегруючи за частинами, дістанемо:

.

З умови 1) теореми випливає, що:

,

.

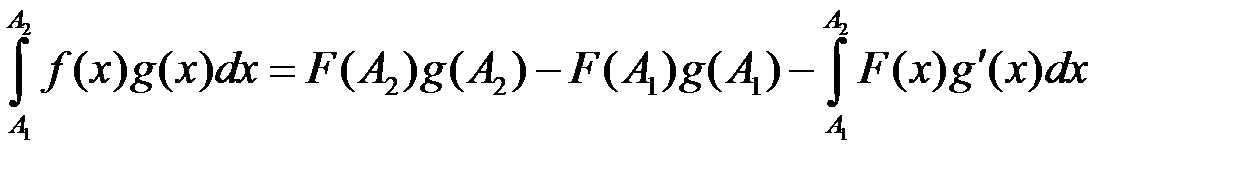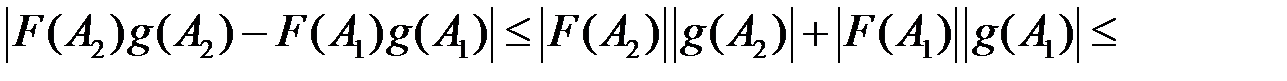
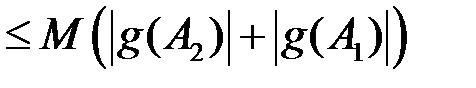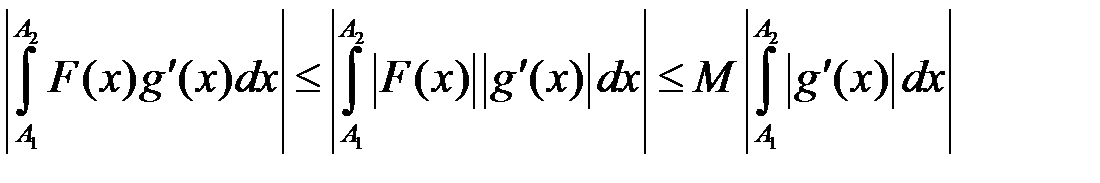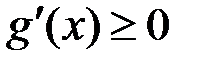Якщо , то 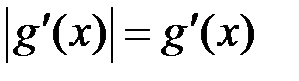, а якщ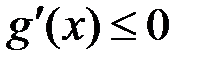о , то 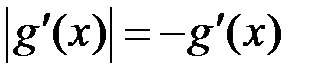. Тому, якщо 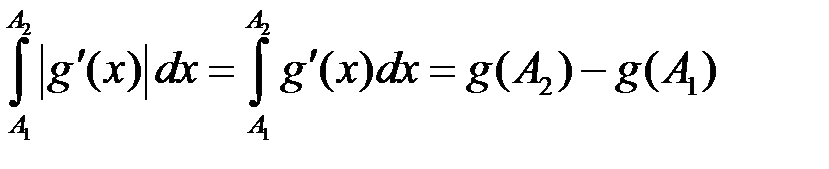, 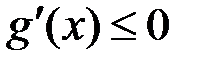то

,

а якщо , то

.

Отже

.

Тому

.

Згідно з умовою 3) теореми: : .

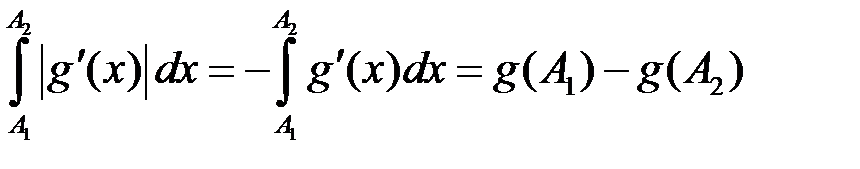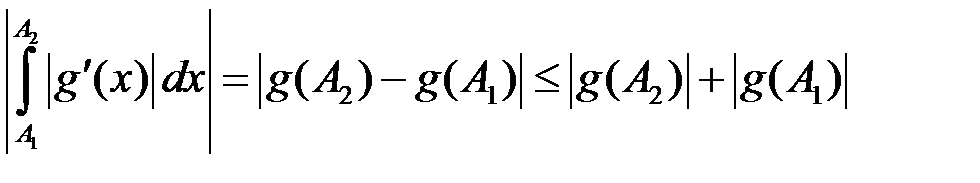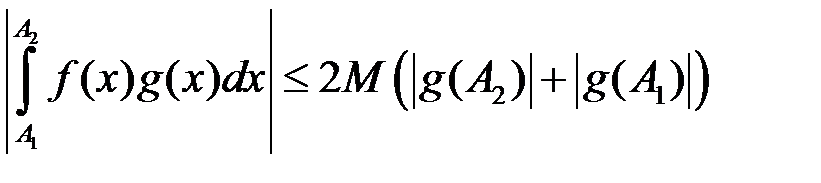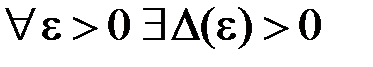
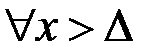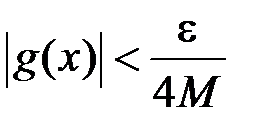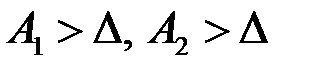Тому, якщо , то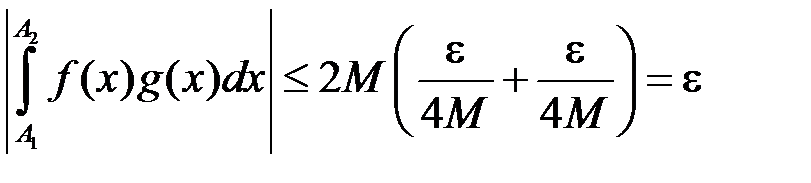

, і таким чином, згідно критерію Коші, інтеграл 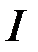збігається.

Теорему доведено.

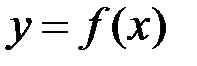Теорема 9 (ознака Абеля). Якщо функція неперервна на проміжку 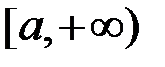, інтеграл 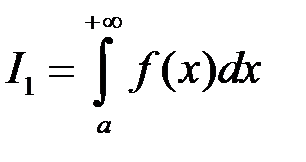збігається, функція 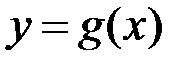обмежена на 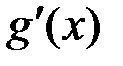, та її похідна зберігає свій знак, то інтеграл 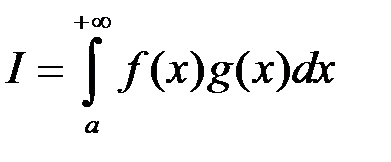збігається.

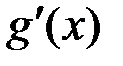Доведення. Оскільки зберігає свій знак, то функція 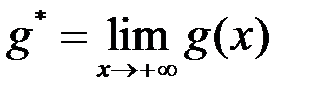монотонна, і за теоремою про границю монотонної та обмеженої функції існує скінченна границя , тому функція 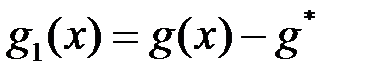монотонно прямує до нуля при 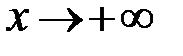. Оскільки інтеграл 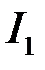збіжний, то функція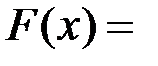 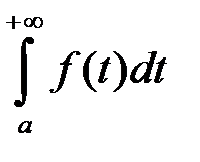обмежена на 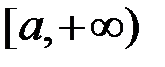. Тоді за ознакою Діріхле інтеграл 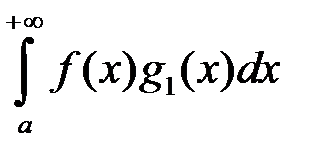. Але оскільки 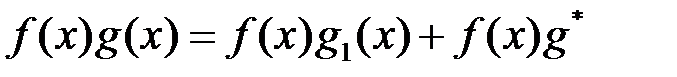, то інтеграл 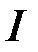також збіжний.

Аналогічні твердження справджуються для невласних інтегралів II роду.

Приклад. Дослідити на збіжність інтеграл

, .

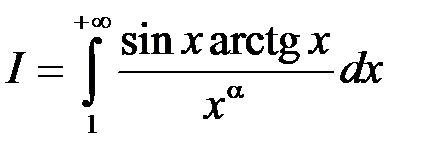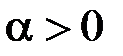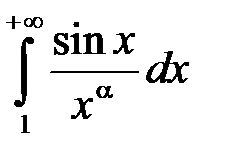Оскільки інтеграл при 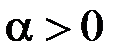збіжний (п. 11, приклад 2), а функція 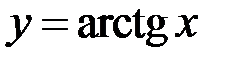обмежена та монотонна, то за ознакою Абеля інтеграл 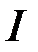збігається.